Лекция 2. Энергия связи ядра. Ядерные силы
2.1. Размеры ядра. Расстояние и энергия в ядерной физике. Следуя рассуждениям Резерфорда, найдем расстояние rmin максимального сближения α-частицы с ядром золота при нулевом прицельном параметре b (или θ = π), отвечающее равенству кинетической энергии α-частицы и энергии кулоновского отталкивания в точке поворота:
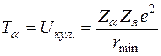 . (2.1)
. (2.1)
Отсюда при Тα = 7,7 МэВ rmin ≈ 3∙10–14 м. Полученный результат есть оценка радиуса атомного ядра, точнее – оценка «сверху». Чтобы установить истинные размеры ядра, нужно увеличивать кинетическую энергию α-частиц и добраться до таких значений Тα, когда начнет нарушаться формула Резерфорда, полученная в предположении о том, что рассеяние происходит в результате кулоновского взаимодействия α-частиц с частицами, несущими заряд Zе.[13] Проведенные много позже эксперименты с α-частицами более высоких энергий показали, что размеры ядра примерно на порядок меньше, т.е. измеряются фемтометрами.[14] Тем не менее, с открытием ядра глубина «проникновения» человека в микромир резко увеличилась (табл. 2.1).
Таблица 2.1.
Характерные размеры макро- и микроскопических объектов
| Размер, м | Объекты |
| > 10-5 | макроскопические тела |
| 10-5-10-6 | грубые дисперсные системы, живые клетки, бактерии |
| 10-6-10-7 | промежуточные дисперсные системы, вирусы |
| 10-7-10-9 | коллоидные системы, макромолекулы |
| 10-9-10-10 | молекулы, атомы |
| 10-14-10-15 | атомные ядра |
| < 10-15 | элементарные частицы |
Метод, позволивший получить вывод о существовании атомного ядра и оценку его размеров, на сегодняшний день типичен для ядерной физики: на тонкую мишень направляют коллимированный пучок частиц и измеряют угловое распределение рассеянных частиц т.е. распределение вероятности их вылета под разными углами. В 1953 г. Американский физик Р. Хофштадтер использовал для исследования пространственного распределения заряда в пределах ядра рассеяние электронов с кинетической энергией 250 МэВ. Опыты Хофштадтера показали, что изменение плотности заряда от центральной области к периферии ядра имеет вид, представленный на рис. 2.1, и описывается функцией следующего вида:
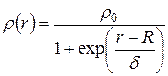 , (2.2)
, (2.2)
где δ < R. Параметр R можно рассматривать как радиус ядра.[15] Эксперименты по рассеянию электронов, протонов и других частиц на ядрах приводят к одной и той же зависимости:
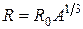 (2.3)
(2.3)
(для массовых чисел А > 20). Среднее из разных опытов значение R0 ≈ 1,3 фм.
Как можно видеть, в ядерной физике изучаются явления, происходящие на очень малых расстояниях и при очень больших энергиях, приходящихся на одну частицу. Верхней границей расстояний, на которых происходят события, изучаемые ядерной физикой, является размер атома, т.е. 10–10 м (или 1Å). Нижней границей энергий отдельных микрочастиц можно считать энергию связи внешних электронов в атоме, т.е. примерно 10 эВ. Для нижней границы расстояний и верхней границы энергий до настоящего времени не установлено каких-либо естественных значений: обе определяются возможностями экспериментальной техники и постепенно смещаются по мере ее развития. В настоящее время минимальные доступные измерения длины имеют порядок 10–18 м, т.е. на восемь порядков меньше размера атома. Максимальная энергия, полученная человеком, составляет 1012 эВ.[16] Таким образом, ядерная физика охватывает огромные области масштабов: 8 порядков по расстояниям и 11 порядков по энергиям.
 2.2. Некоторые соотношения релятивистской механики.[17] При больших энергиях отдельных частиц классическая механика перестает быть справедливой и должна быть заменена более строгой (при данных условиях) теорией – механикой теории относительности, или релятивистской механикой.
2.2. Некоторые соотношения релятивистской механики.[17] При больших энергиях отдельных частиц классическая механика перестает быть справедливой и должна быть заменена более строгой (при данных условиях) теорией – механикой теории относительности, или релятивистской механикой.
Согласно релятивистской механике, ни один физический объект не может двигаться со скоростью, превышающей скорость света в вакууме: с ≈ 3·108 м/с. Релятивистские эффекты можно не учитывать, если скорость объекта v пренебрежимо мала по сравнению со скоростью света. Если же отношение β = v/c не исчезающее мало по сравнению с единицей (например, 0,1), релятивистские поправки становятся заметными. Такая ситуация довольно часто имеет место в физике атомного ядра. Наконец, если β имеет порядок единицы, характер движения будет существенно релятивистским.
Со шкалой расстояний, которая рассматривалась в предыдущем разделе, тесно связана естественная шкала времени. Размеры ядра (R) и скорость света определяют характерное время в ядерной физике – т.н. ядерное время, равное времени пролета релятивистской частицы через ядро,
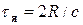 , (2.4)
, (2.4)
т.е. около 10–22 с. Для атомного ядра все времена t >> τя являются большими.
Приведем релятивистские соотношения, выражающие энергию Е и импульс p частицы с массой M через ее скорость:
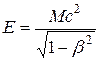 , (2.5)
, (2.5)
 . (2.6)
. (2.6)
Одним из фундаментальных следствий формулы (2.5) является знаменитое соотношение Альберта Эйнштейна
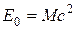 , (2.7)
, (2.7)
связывающее полную энергию покоящейся изолированной физической системы (энергию покоя Е0) с ее массой. Универсальное соотношение (2.7) выражает эквивалентность массы и энергии: зная массу, можно определить энергию покоящейся системы, и наоборот. Энергия покоя является инвариантом, т.е. величиной, не зависящей от выбора системы координат.
Из формул (2.5) и (2.6) легко получить следующее:
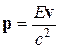 . (2.8)
. (2.8)
При движении частица приобретает дополнительную (кинетическую) энергию, поэтому ее полная энергия увеличивается. При скорости v = с энергия и импульс, согласно (2.5-2.6), обращаются в бесконечность. Однако, если масса частицы равна нулю, бесконечности не получается. Поэтому для фотонов, а также для ультрарелятивистских частиц, т.е. для частиц с 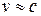 из (2.8) следует, что
из (2.8) следует, что
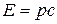 . (2.9)
. (2.9)
Связь энергии с массой и импульсом движущейся частицы выражается соотношением, которое получается из (2.5-2.6) путем исключения скорости:
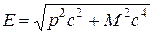 . (2.10)
. (2.10)
Для покоящейся частицы p = 0, и выражение (2.10) совпадает с (2.7). Если же энергия покоя Mc2 много меньше, чем pc, имеем соотношение (2.9).
Релятивистская кинетическая энергия получается вычитанием энергии покоя из полной энергии:
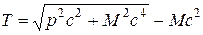 . (2.11)
. (2.11)
Критериями применимости классической механики, эквивалентными v << с, являются условия p << Mc и T << E0.
2.3. Энергия связи ядра.Атомное ядро – система связанных нуклонов. Чтобы разделить его на составляющие протоны и нейтроны, нужно затратить некоторую минимальную энергию W(A, Z), называемую энергией связи ядра.В соответствии с релятивистским законом (2.7) взаимосвязи массы покоящейся частицы и энергии покоя, энергия связи ядра определяется следующим образом:
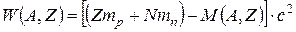 , (2.12)
, (2.12)
где М(A, Z) – масса ядра. Выражение в квадратных скобках, т.е.
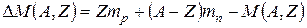 , (2.13)
, (2.13)
называется дефектом массы ядра. Согласно (2.12) устанавливается следующая связь между дефектом массы в а.е.м. и энергией связи в МэВ:
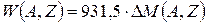 . (2.14)
. (2.14)
Стоящий в (2.14) коэффициент 931,5 МэВ/а.е.м. называется энергетическим эквивалентом атомной единицы массы.[18]
 Энергия связи ядра тем больше, чем больше число нуклонов А. В связи с этим удобно иметь дело с удельной энергией связи – энергией связи на один нуклон,
Энергия связи ядра тем больше, чем больше число нуклонов А. В связи с этим удобно иметь дело с удельной энергией связи – энергией связи на один нуклон,
 . (2.15)
. (2.15)
График этой величины[19] представлен на рис. 2.2. При А > 11 удельная энергия связи лежит в пределах от 7,4 до 8,8 МэВ. Наибольшее значение (т.н. «железный максимум») приходится на область массовых чисел А ≈ 60 (железо, кобальт, никель). Среди наиболее легких ядер наблюдаются нерегулярные изменения удельной энергии связи. В частности, энергии связи 4Не, 12С и 16О аномально высоки, а 6Li, 10B 14N – аномально низки. В дейтроне (ядре дейтерия: D, или 2Н) удельная энергия связи наименьшая (1,112 МэВ).
Энергия любой химической связи составляет единицы эВ. В связи с этим с точки зрения запасов энергии 1 г ядерного топлива эквивалентен примерно 1 т топлива химического. Получить ядерную энергию можно двумя способами: синтезом легких ядер и делением тяжелых ядер. В обоих процессах (показаны стрелками на рис. 2.2) совершается переход к ядрам с большей энергией связи, поэтому часть ее высвобождается в виде кинетической энергии продуктов.
2.4. Ядерные силы.Нуклоны внутри ядра удерживаются ядерными силами. Их происхождение связано с особым взаимодействием, получившим в физике название сильного. Значение ε характеризует величину сильного взаимодействия. Укажем здесь для сравнения, что энергия кулоновского отталкивания двух протонов в ядре, равная

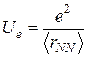 , (2.16)
, (2.16)
где 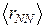 ≈ 2фм (среднее расстояние между нуклонами в ядре), составляет около 0,7 МэВ, что примерно на порядок меньше ε.
≈ 2фм (среднее расстояние между нуклонами в ядре), составляет около 0,7 МэВ, что примерно на порядок меньше ε.
Некоторые другие свойства ядерных сил можно установить, используя уже известные результаты. Так, например, очевидно, что ядерные силы – это силы короткодействующие: на расстояниях, существенно превышающих характерные размеры ядра, они равны нулю. Это показывают, например, опыты Резерфорда: при энергиях ~ 10 МэВ рассеяние одного ядра (α-частицы) на другом происходит так, как будто между ними действует только кулоновская сила.
На расстоянии порядка нескольких фм ядерные силы – силы притяжения. В противном случае нуклоны не образовывали бы связанные системы – атомные ядра. Отталкивающий характер ядерных сил на расстояниях < 0,5 фм (далеко не очевидный[20]) был установлен лишь при изучении столкновений нуклонов с энергиями в сотни МэВ. Зависимость потенциала сильного взаимодействия Us от расстояния между нуклонами показана на рис. 2.3.
Ядерные силы обладают свойством насыщения. При увеличении числа нуклонов в ядре удельная энергия связи ε быстро достигает предельного значения и далее меняется уже очень мало (рис. 2.2.), т.е. энергия связи W пропорциональна A. Такое поведение W означает, что каждый нуклон внутри ядра взаимодействует не со всеми, а лишь с ближайшими нуклонами. В противном случае энергия связи W была бы пропорциональна как общему числу нуклонов, так и числу связей каждого отдельного нуклона со всеми остальными, т.е. A(A – 1) ≈ A2.
Еще одним свойством ядерных сил является их зарядовая независимость. Как показывают опыты по нуклон-нуклонному рассеянию, взаимодействие n-n, p-p и n-p одинаково[21], если в каждом случае учесть влияние сил электромагнитной природы (главным образом, кулоновское отталкивание в случае протонов). К тому же выводу приводит рассмотрение энергии в зеркальных ядрах, т.е. таких, которые «получаются»друг из друга путем замены всех протонов на нейтроны и наоборот (например, 39К и 39Са).
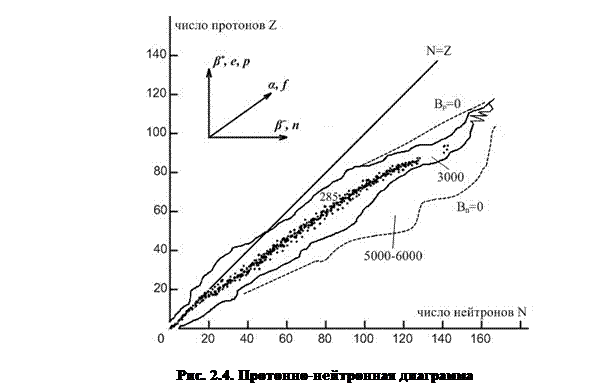 2.5. Протонно-нейтронная диаграмма.Всего существует в природе или получено искусственно около 3000 различных нуклидов. Диапазон изменений Z и A для известных ядер: 1–118 и 1–293, соответственно. Условно нуклиды можно разделить на две группы.
2.5. Протонно-нейтронная диаграмма.Всего существует в природе или получено искусственно около 3000 различных нуклидов. Диапазон изменений Z и A для известных ядер: 1–118 и 1–293, соответственно. Условно нуклиды можно разделить на две группы.
1) Стабильные и долгоживущие (всего их 285). Долгоживущими принято считать нуклиды со средним временем жизни[22] > 5∙108 лет, что обеспечивает их ненулевое процентное содержание в природной смеси изотопов.
2) Радиоактивные. Для этой категории среднее время жизни < 5∙108 лет. Некоторые из них существуют в природе в малых количествах вследствие непрерывного образования при распаде долгоживущих нуклидов или в ядерных реакциях. Большинство же радиоактивных нуклидов получается искусственно.
На рис. 2.4. изображена протонно-нейтронная диаграмма ядер. Каждому стабильному или долгоживущему нуклиду на плоскости (NZ) соответствует точка, совокупность которых называется линией, или дорожкой стабильности. Легкие стабильные ядра следуют линии N = Z, а для тяжелых стабильных ядер N > Z. Как будет показано в следующем разделе, за такой ход дорожки стабильности отвечает кулоновское отталкивание протонов в ядре. Без него для всех стабильных ядер было бы N ≈ Z.
Сплошная линия на диаграмме ограничивает область известных ядер, а пунктирная – всю область ядер, которые по теоретическим оценкам можно получить искусственно (их от 5 до 6 тысяч). Границы этой области образуют ядра, для которых энергия отделения протона
 (2.17)
(2.17)
или нейтрона
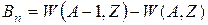 (2.18)
(2.18)
(минимальная энергия, которую нужно затратить, чтобы удалить нуклон из ядра) равна нулю. Добавляемый нуклон просто не будет удерживаться такими ядрами. Таким образом, за границами Bp = 0 и Bn = 0 ядра существовать не могут.
2.6. Капельная модель ядра. Формула Вайцзеккера.Описание свойств атомного ядра на основе законов взаимодействия между нуклонами является центральной проблемой теоретической ядерной физики. Однако представления о структуре ядер значительно беднее, чем представления об атомной и молекулярной структуре. Последние понятны настолько глубоко и полно, что дают возможность рассчитывать практически любую характеристику объекта, построенного из ядер и электронов. В то же время, хотя сегодня знания об атомном ядре нельзя назвать ничтожными, они все же еще недостаточны для построения законченной картины.
В первую очередь, это связано с тем, что количественная теория сильного взаимодействия до сих пор не создана, и вид ядерных сил приходится подбирать путем подгонки к экспериментальным данным.В атомной физике «богатые» атомные спектры дают возможность это сделать до конца, и если бы о виде электромагнитного взаимодействия ничего не было известно, его можно было бы установить из спектров. Однако существует лишь одна связанная система из двух нуклонов – дейтрон, имеющий единственный энергетический уровень. Этого, разумеется, недостаточно для построения теории ядра.
Дополнить информацию можно путем экспериментов по рассеянию нуклонов друг на друге. Но даже по всей совокупности экспериментальных данных точный вид взаимодействия может быть установлен лишь тогда, когда силы, действующие между частицами, не зависят от их скоростей, т.е. являются потенциальными. Для нуклонов это не так.[23]
Наконец, взаимодействие между двумя нуклонами изменяется, когда они находятся в поле других нуклонов. О роли тройных и вообще множественных сил в ядре мало что известно. Современная теория предсказывает их существование, но не дает возможность рассчитать интенсивность.
Эти и другие трудности можно обойти, используя модельные представления. В моделях ядра заранее задаются или угадываются некоторые его свойства. При этом часто используются аналогии с другими физическими объектами, на первый взгляд, не имеющими ничего общего с ядром. Так,свойство насыщения ядерных сил, следующее из их короткодействия, притяжения на больших и отталкивания на малых расстояниях, делает ядро похожим на каплю жидкости. Силы, связывающие молекулы жидкости, тоже насыщаются, а энергия испарения капли линейно увеличивается с увеличением ее массы. На этом основании был создан способ описания свойств ядра в модели жидкой капли (К. Вайцзеккер, 1935 г.).
В рамках капельной модели Вайцзеккера получается полуэмпирическая формула для энергии связи ядра как функции его протонно-нейтронного состава. В эту формулу входят следующие слагаемые.
1) Объемная энергия. Энергия связи ядра тем больше, чем больше в нем нуклонов, или, другими словами, объем ядра V, так как V = (4/3)πR3 ~ A. Поэтому в первом приближении энергия связи ядра равна
 , (2.19)
, (2.19)
где α > 0 – константа. Если этим ограничиться, то мы имеем дело с бесконечной ядерной материей (поверхностные эффекты несущественны), лишенной заряда (пренебрегаем кулоновским отталкиванием протонов).
2) Поверхностная энергия. Нуклоны на поверхности ядра связаны менее сильно, чем внутри, так как взаимодействуют с меньшим числом своих соседей. Если в бесконечной ядерной материи провести сферическую поверхность, ограничивающую ядро, и отбросить нуклоны вне ее, то оставшиеся у поверхности нуклоны ядра потеряют примерно половину своих связей. Число потерянных связей пропорционально площади поверхности, равной S = 4πR2 ~ A2/3. Тогда в (2.19) следует добавить слагаемое, пропорциональное A2/3, со знаком «минус»
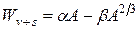 , (2.20)
, (2.20)
где β > 0 – константа. На поверхностный нуклон действует результирующая сила, направленная внутрь ядра. Поэтому поверхностные нуклоны стремятся сжать ядро, создавая, как в капле жидкости, поверхностное натяжение.
3) Кулоновская энергия. Эту энергию можно оценить, если рассматривать заряд, однородно распределенный по объему сферы. Тогда энергия отталкивания протонов, уменьшающая W, дается классической электростатической формулой
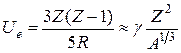 (2.21)
(2.21)
(знак примерного равенства соответствует Z >>1). В итоге
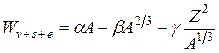 . (2.22)
. (2.22)
4) Энергия симметрии. Ограничиваясь выражением (2.22), нельзя получить правильный ход линии стабильности. Энергия связи является мерой устойчивости ядра, а, согласно (2.22), максимум W достигается при Z = 0, т.е. самые стабильные ядра должны состоять из одних лишь нейтронов. Чтобы получить правильный результат, необходимо учесть, что в легких стабильных ядрах Z = N, и ввести в формулу для энергии связи слагаемое, уменьшающее W при нарушении протонно-нейтронной симметрии. Хорошее согласие с экспериментом достигается, если положить
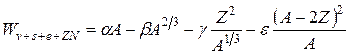 . (2.23)
. (2.23)
5) Энергия спаривания. С помощью формулы (2.23) можно описать энергию связи ядер (за исключением самых легких, c A < 20) с точностью до 1%. Однако в экспериментальных результатах имеются «пульсации» на уровне 1-2 МэВ. Так, энергия отделения нейтрона для некоторых изотопов периодически возрастает, когда число N становится четным, и уменьшается при нечетных N. Следовательно, каждый из нуклонов ядра наиболее сильно связан с остальными, если объединен в пару с другим таким же, а оставшийся одиночный нуклон связан слабее. С точки зрения эффекта спаривания все ядра разбиваются на три группы.
– Четно-четные ядра (c четными Z и N). Все нуклоны спарены, добавка к W положительна.
– Нечетно-нечетные ядра (c нечетными Z и N). Не спарено по одному нуклону каждого типа, добавка к W отрицательна.
– Ядра с нечетным A. Один из нуклонов не спарен, добавка к W равна нулю (условленная точка отсчета).
Четно-нечетные ядра являются наиболее устойчивыми, а нечетно-нечетные, напротив, самыми неустойчивыми: стабильных ядер в этой группе всего четыре: 2H, 6Li, 10B, 14N. Приведем распределение числа стабильных и долгоживущих ядер в зависимости от значений Z и N (табл. 2.2).
С учетом спаривания нуклонов одного типа наилучшее воспроизведение экспериментальных величин энергии связи дает следующая формула:
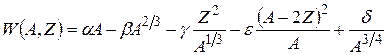 , (2.24)
, (2.24)
где α = 15,75 МэВ, β = 17,8 МэВ, γ = 0,71 МэВ, ε = 23,7 МэВ, δ = 0 для ядер с нечетным А, 34 МэВ для четно-четных и –34 МэВ для нечетно-нечетных ядер.
Таблица 2.2
Распространенность ядер в зависимости от значений Z и N
| Z | N | А | Число стабильных и долгоживущих ядер |
| четное | четное | четное | |
| нечетное | четное | нечетное | |
| четное | нечетное | нечетное | |
| нечетное | нечетное | четное | |
| Всего: 285 |
Формула (2.24) носит название формулы Вайцзеккера. Отметим, что четвертое и пятое слагаемые в (2.24) уже не связаны с представлением о ядре как о капле несжимаемой заряженной жидкости. Их появление – результат эмпирически установленных закономерностей, находящих свое объяснение в другой модели – модели ядерных оболочек (см. Лекцию 3).
Формула Вайцзеккера дает правильное представление об энергии связи: для А > 40 расхождение с результатами измерений W не превышает 0,1%. Таким образом, модель позволяет предсказать энергетические условия радиоактивного распада того или другого вида. В частности, с ее помощью можно достаточно точно определить положение линии стабильности на протонно-нейтронной диаграмме. Для этого достаточно, зафиксировав массовое число A, найти изобар с наибольшей энергией связи. Дифференцируя (2.24) по Z и приравнивая к нулю производную, после подстановки параметров получаем, что
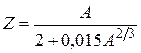 . (2.25)
. (2.25)
Условие (2.25) определяет в рамках модели Вайцзеккера соотношение между числом протонов и нейтронов для ядер, устойчивых относительно β-распада (дорожка стабильности). Ядра, содержащие избыток протонов, нестабильны относительно β+-распада
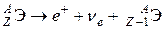 ,
,
а ядра с избытком нейтронов – относительно β–-распада[24]
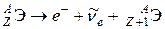 .
.
Дата добавления: 2015-05-26; просмотров: 3820;
