Лекция 4. Квантовые свойства ядер
4.1. Энергия симметрии в ОМО. Объяснение закономерностей, связанных с магическими числами, стало далеко не единственным успехом ОМО. Так, например, одним из слагаемых в формуле Вайцзеккера для энергии связи ядра является энергия симметрии. Эта поправка, эмпирическая в рамках капельной модели, находит свое объяснение в ОМО.
 Рассмотрим упрощенную модель ядра в виде нуклонов в потенциальной яме с эквидистантной последовательностью уровней; последние одинаковы для протонов и нейтронов. Пусть вначале ядро состоит из равного количества нуклонов обоих видов (N = Z). Будем, начиная с самого верхнего протонного уровня, последовательно «превращать» протоны в нейтроны, перемещая их при этом на самые нижние свободные уровни для нейтронов. В результате такой операции замена первого протона на нейтрон приведет к увеличению энергии ядра на ΔЕ, второго – на 3ΔЕ, третьего – на 5ΔЕ, и т.д. (рис. 4.1). Можно видеть, что в общем случае суммарное увеличение энергии определяется площадью треугольника ОXY, т.е. пропорционально (N – Z)2. Очевидно, то же самое получится и при замене нейтронов на протоны.
Рассмотрим упрощенную модель ядра в виде нуклонов в потенциальной яме с эквидистантной последовательностью уровней; последние одинаковы для протонов и нейтронов. Пусть вначале ядро состоит из равного количества нуклонов обоих видов (N = Z). Будем, начиная с самого верхнего протонного уровня, последовательно «превращать» протоны в нейтроны, перемещая их при этом на самые нижние свободные уровни для нейтронов. В результате такой операции замена первого протона на нейтрон приведет к увеличению энергии ядра на ΔЕ, второго – на 3ΔЕ, третьего – на 5ΔЕ, и т.д. (рис. 4.1). Можно видеть, что в общем случае суммарное увеличение энергии определяется площадью треугольника ОXY, т.е. пропорционально (N – Z)2. Очевидно, то же самое получится и при замене нейтронов на протоны.
Результат качественно не изменится, если учесть наличие у нуклонов спина S = ½ и производить операцию попарного превращения одних нуклонов в другие с соответствующим перемещением. Однако в последнем случае поправка к энергии будет в два раза меньше из-за двукратного вырождения по направлению спина. Тогда для уточнения зависимости достаточно вспомнить, что большинство одночастичных уровней, даже с учетом спин-орбитального взаимодействия, многократно вырождены по угловому моменту J, причем кратность вырождения g верхних уровней тем больше, чем больше нуклонов в ядре. В первом приближении можно считать, что g ~ A. Тогда поправка к формуле (2.24), связанная с протнно-нейтронной симметрией, равна
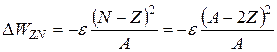 .
.
4.2. Спин и четность основных состояний ядер в ОМО. Эффект спаривания.Другим успехом ОМОстала ее способность описания квантовых свойств ядер в основном состоянии: спина, магнитного момента, четности. В частности, ОМО способна однозначно предсказать спин и четность основного состояния ядра в трех следующих случаях.
1) Ядро с заполненными уровнями (подоболочками). Так как на каждой из подоболочек заняты все состояния со всеми возможными проекциями вектора углового момента J, каждому нуклону с проекцией +jz соответствует нуклон с проекцией –jz. Таким образом, результирующий угловой момент ядра, т.е. спин ядра, равен нулю. Четность замкнутой подоболочки положительна, так как она образована парами нуклонов с одинаковой четностью. Таким образом, для замкнутой подоболочки
 . (4.1)
. (4.1)
2) Ядро с одним нуклоном сверх заполненных подоболочек. Остов заполненных подоболочек имеет характеристики 0+, и спин и четность определяются квантовыми числами единственного внешнего нуклона. Если этот нуклон находится в состоянии nlj, то спин ядра равен j, а четность P = (–1)l. Поэтому для основного состояния такого ядра
 . (4.2)
. (4.2)
3) Ядро с вакансией в заполненной подоболочке. Такому ядру для заполнения подоболочки не хватает одного нуклона. Пусть состояние нуклона на такой подоболочке будет nlj. Обозначим момент и четность подоболочки с вакансией как j’ и P’. Так как добавление нуклона на подоболочку с вакансией замыкает ее, то J + J’ = 0 и P∙P’ = +1, откуда j’ = j и P’ = P, т.е. имеем те же правила (4.2) нахождения спина и четности основного состояния, что и для ядра с одним нуклоном сверх замкнутых подоболочек.
Рассмотрим случай двух тождественных нуклонов на одной подоболочке. Вся совокупность экспериментальных данных говорит о том, что в основном состоянии ядра нуклоны одного сорта на подоболочке объединяются в пары с противоположными jz; моменты таких пар протонов и нейтронов, очевидно, равны нулю. Таким образом, между парой нуклонов на одной подоболочке в основном состоянии существует дополнительное взаимодействие, не сводящееся к центрально-симметричному потенциалу UССП. Его называют остаточным. Остаточное взаимодействие проявляет себя таким образом, что паре нуклонов при указанных условиях энергетически выгодно иметь нулевой результирующий момент. Другими словами, оно снимает вырождение по j для этой пары, так что низшим по энергии оказывается состояние с нулевым суммарным моментом. Это и есть уже упоминавшийся при обсуждении формулы Вайцзеккера эффект спаривания. Следовательно, можно отметить, что ядерные силы зависят от квантовых состояний нуклонов.
При заполнении подоболочки в основном состоянии нуклоны одного сорта последовательно формируют пары с одинаковыми по величине и противоположными по знаку проекциями момента: величина и знак проекции момента четного нуклона «подстраиваются» так, чтобы скомпенсировать величину и знак момента нечетного нуклона. На рис. 4.2 в качестве примера приведено строение верхних нейтронных подоболочек в изотопах аргона. Проекции момента нейтрона условно обозначены стрелками. По мере увеличения N заселение уровней идет сверху вниз и слева направо; на уровне 1f7/2 отмечены вакансии. В табл. 4.1 приведены значения спинов и четностей 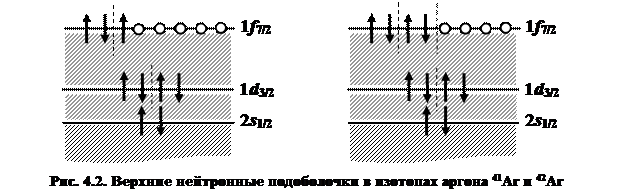 для ядер 33Ar–42Ar. Из сравнения рис. 4.1. и табл. 4.1 видно, что именно эффект спаривания приводит к наблюдаемым экспериментально значениям J и Р.
для ядер 33Ar–42Ar. Из сравнения рис. 4.1. и табл. 4.1 видно, что именно эффект спаривания приводит к наблюдаемым экспериментально значениям J и Р.
Таблица 4.1.
Квантовые характеристики изотопов аргона в основном состоянии
| Конфигурация остова | A | N | N’ * | J | P |
| [(1s1/2)2 (1p3/2)4 (1p1/2)2 (1d5/2)6 (2s1/2)2 (1d3/2)2]p [(1s1/2)2 (1p3/2)4 (1p1/2)2 (1d5/2)6]n | 1/2 | + | |||
| + | |||||
| 3/2 | + | ||||
| + | |||||
| 3/2 | + | ||||
| + | |||||
| 7/2 | – | ||||
| + | |||||
| 7/2 | – | ||||
| + |
* Число нейтронов, не входящих в остов
Если на подоболочке находится четное число нуклонов, то ее момент равен нулю, а если нечетное,то он равен j. С учетом этого легко сформулировать правила для спинов и четностей ядер в основном состоянии. А именно, для четно-четных ядер справедливо выражение (4.1), а для ядер с нечетными А – (4.2). Что касается нечетно-нечетных ядер, то для них
 , (4.3)
, (4.3)
где индексы p и n у квантовых чисел относятся к протонам и нейтронам соответственно. Таким образом, на основании только ОМО предсказать спин основного состояния нечетно-нечетного ядра однозначно не удается: можно лишь утверждать, что он равен одному из допустимых целочисленных значений. Так, согласно ОМО, в 22Na и 24Na неспаренные протон и нейтрон находятся на подоболочке 1d5/2. Следовательно, эти ядра в основном состоянии должны иметь положительную четность и спин от 0 до 5. Экспериментально установленные квантовые характеристики 22Na и 24Na – это 3+ и 4+ соответственно.
4.3. Магнитные моменты ядер.В результате орбитального движения электрически заряженной частицы возникает магнитный дипольный момент μ, или просто магнитный момент, величина и знак которого определяют энергию взаимодействия этой частицы с внешним магнитным полем B:
 . (4.4)
. (4.4)
Так, например, при движении протона с орбитальным моментом L возникает магнитный момент
 . (4.5)
. (4.5)
Величина μЯ = eћ/2mpc называется ядерным магнетоном. Ядерный магнетон служит естественной единицей измерения магнитных моментов ядер. Напомним, что в атомной физике аналогичная величина для электрона, μБ = eћ/2mec, называется магнетоном Бора.
Магнитный момент существует и для заряженной частицы с l = 0, если ее спин отличен от нуля. Как было теоретически показано П. Дираком (1930 г.), магнитный момент электрона равен gμБ, где g = 2 – гиромагнитный, или g-фактор частицы со спином 1/2. Исходя из этого, можно было бы ожидать, что спиновый магнитный момент протона равен 2μЯ. Однако в действительности он оказывается в 2,793 раза больше, т.е. gp = 5,586. То, что предсказание теории Дирака, рассматривающей протон как бесструктурную частицу, не согласуется с опытом, заставляет предположить, что на самом деле протон является не таким уж «простым» образованием. То, что нуклоны имеют внутреннюю структуру, подтверждается и результатом измерений магнитного момента нейтрона: гиромагнитный фактор gn = –3,826 (Л. Альварец, Ф. Блох, 1940 г.). Знак «минус» в данном случае означает, что векторы спина и магнитного момента направлены в противоположные стороны. Наличие у нейтрона ненулевого магнитного момента позволяет заключить, что внутри этой частицы существует некоторое распределение компенсирующих друг друга зарядов, причем, как показывают эксперименты по рассеянию быстрых электронов на нейтронах атомного ядра, отрицательный заряд «размазан» по периферии, а положительный сконцентрирован в центральной области. Зарядовая структура нейтрона объясняется его кварковым строением (см. Лекцию 18).
Магнитный момент ядра со спином J, состоящего из A нуклонов, имеет, таким образом, орбитальную и спиновую составляющие: [32]
 . (4.6)
. (4.6)
У четно-четных ядер магнитный момент равен нулю: моменты каждой пары нуклонов одного сорта компенсируют друг друга. У всех других ядер, которые называют магнитными, он зависит не только от величины спина, но и от взаимной ориентации спиновой и орбитальной составляющей. Величину ядерного g-фактора gЯ лишь в редких случаях удается достаточно точно рассчитать теоретически.
 Основным методом измерения gЯ является метод ядерного магнитного резонанса (ЯМР). В отсутствие магнитного поля основное состояние ядра со спином J ≠ 0 вырождены (2J + 1)-кратно. При включении однородного магнитного поля достаточно высокой напряженности эти состояния становятся энергетически неэквивалентными. Так, например, двукратно вырожденный уровень протона (J = 1/2) расщепляется, образуя энергетический дуплет (рис. 4.3). Согласно (4.4), величина расщепления ΔЕ пропорциональна напряженности магнитного поля и зависит от магнитных свойств ядра. Для 1Н
Основным методом измерения gЯ является метод ядерного магнитного резонанса (ЯМР). В отсутствие магнитного поля основное состояние ядра со спином J ≠ 0 вырождены (2J + 1)-кратно. При включении однородного магнитного поля достаточно высокой напряженности эти состояния становятся энергетически неэквивалентными. Так, например, двукратно вырожденный уровень протона (J = 1/2) расщепляется, образуя энергетический дуплет (рис. 4.3). Согласно (4.4), величина расщепления ΔЕ пропорциональна напряженности магнитного поля и зависит от магнитных свойств ядра. Для 1Н
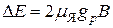 . (4.7)
. (4.7)
При переходе ядра с нижнего энергетического уровня на верхний энергия ΔЕ поглощается, а при обратном переходе выделяется. В этих переходах и заключается смысл ЯМР. Возможность его экспериментального наблюдения связано с тем, что заселенность уровней неодинакова: система из множества магнитных ядер подчиняется законам статистической термодинамики, что влечет за собой увеличение заселенности нижнего уровня. В соответствии с принципом Больцмана разность заселенностей уровней равна ≈ ΔЕ/kБT, где Т – абсолютная температура. При обычных температурах и полях разность заселенностей не превышает 10–5 от общего числа магнитных ядер, т.е. весьма незначительна. Тем не менее, если наряду с однородным магнитным полем приложить к такой системе переменное электрическое поле с частотой ω = ΔЕ/ħ, то будет происходить резонансное поглощение энергии этого поля.[33] Эксперимент ЯМР состоит в регистрации поглощения радиотехническими средствами, давая возможность определить по значению резонансной частоты ω величину магнитного момента.
Для ядра, окруженного атомными электронами, приложенное магнитное поле экранируется ими: движение электронов индуцирует магнитное поле B’, направленное противоположноB. Поэтому для осуществления резонанса на частоте ω необходимо приложить несколько большее магнитное поле: B + B’.[34] Такое смещение сигнала называется химическим сдвигом. Химический сдвиг определяется строением электронных оболочек атома. Образование атомом химических связей отражается на его величине. В молекуле взаимодействие магнитных моментов соседних ядер (спин-спиновая связь) ведет к расщеплению линий резонансного поглощения. В результате спектры ЯМР несут богатую информацию о химической связи атома с магнитным ядром. Явление ЯМР представляет, таким образом, ценнейший инструмент для изучения строения молекул, идентификации химических соединений и т.п. В органической химии широко используется магнитный резонанс на ядрах 1Н, 13C и некоторых других.
Взаимодействие магнитного момента ядра с магнитными моментами электронов приводит также к сверхтонкому расщеплению линий в оптическом спектре атома. Это дает возможность определить величину магнитного момента ядра (по величине расщепления) и спина ядра (по количеству линий расщепления).
4.4. Электрический квадрупольный момент. Равновесные формы ядер. Электрический дипольный момент ядра
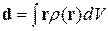 (4.8)
(4.8)
тождественно равен нулю: распределение электрического заряда ρ(r) для ядра, обладающего определенной четностью, есть четная функция r, и интеграл в (4.8) обращается в 0. Однако ядро может обладать ненулевым электрическим квадрупольным моментом, определяемым как
 . (4.9)
. (4.9)
Простейшей моделью квадруполя является пара равных противоположно ориентированных диполей d= er, расположенных на расстоянии r друг от друга (рис. 4.4-а). Такая система обладает квадрупольным моментом Q = 2er2. Поэтому значение квадрупольного момента, отнесенное к единичному заряду, измеряется в единицах площади.
Отличный от нуля квадрупольный момент ядра можно обнаружить, помещая его в неоднородное (например, в направлении z) электрическое поле. Тогда у ядра возникает дополнительная энергия взаимодействия с полем, пропорциональная Q∙(∂E/∂z), где E – напряженность поля. Неоднородное электрическое поле способны создавать, в частности, атомные электроны. В этом случае, как и при μ≠ 0, в спектре атома появляется сверхтонкое расщепление линий. Существует и метод измерения резонансной частоты поглощения, аналогичный методу ЯМР.
 Величина Q представляет меру отклонения распределения заряда ρ(r) от сферически симметричного, т.е. характеризует равновесную форму ядра (рис. 4.4-б, в). Измерения электрических квадрупольных моментов множества ядер позволили установить, что большинство их не имеют сферической формы, а представляют собой эллипсоиды вращения: вытянутые при Q > 0 и сплюснутые при Q < 0. Чаще встречается вытянутая форма. Она наиболее характерна для ядер, у которых число протонов Z лежит посередине между двумя соседними магическими числами (примером могут служить ядра редкоземельных элементов, для которых 50 < Z < 82). Наибольшие по абсолютной величине значения Q также наблюдаются у вытянутых ядер. Максимальное и минимальное значения Q зарегистрированы у следующих ядер в основных состояниях: 176Lu (800 фм2) и 233Pa (–300 фм2). Отметим, что эти величины в десятки раз больше, чем квадраты радиусов соответствующих ядер. Это означает, что квадрупольные моменты обусловлены коллективным движением многих нуклонов ядра.
Величина Q представляет меру отклонения распределения заряда ρ(r) от сферически симметричного, т.е. характеризует равновесную форму ядра (рис. 4.4-б, в). Измерения электрических квадрупольных моментов множества ядер позволили установить, что большинство их не имеют сферической формы, а представляют собой эллипсоиды вращения: вытянутые при Q > 0 и сплюснутые при Q < 0. Чаще встречается вытянутая форма. Она наиболее характерна для ядер, у которых число протонов Z лежит посередине между двумя соседними магическими числами (примером могут служить ядра редкоземельных элементов, для которых 50 < Z < 82). Наибольшие по абсолютной величине значения Q также наблюдаются у вытянутых ядер. Максимальное и минимальное значения Q зарегистрированы у следующих ядер в основных состояниях: 176Lu (800 фм2) и 233Pa (–300 фм2). Отметим, что эти величины в десятки раз больше, чем квадраты радиусов соответствующих ядер. Это означает, что квадрупольные моменты обусловлены коллективным движением многих нуклонов ядра.
Дважды магические ядра – ядра сферические; в целом же сферических ядер мало. В интервале между соседними магическими числами ядра меняют форму в такой последовательности: сферическое, сплюснутое, сферическое, вытянутое, сильно вытянутое, вытянутое, сферическое.
Одночастичная модель оболочек, объясняя квантовые характеристики ядер в основном состоянии, находится в противоречии с экспериментом, когда речь идет о равновесной форме ядра (а также о возбужденных состояниях). Главная причина – пренебрежение остаточным нуклон-нуклонным взаимодействием, которое нельзя свести к одинаковому для всех нуклонов сферически симметричному потенциалу. Одно из проявлений остаточных сил – эффект спаривания, однако остаточные силы не сводятся только к силам спаривания. В наиболее общей и наиболее современной модели ядра – многочастичной модели оболочек (ММО) – подбирается не только самосогласованный, но и остаточный потенциал. ММО очень громоздка математически, но обладает большей предсказательной силой.
4.5. Возбужденные состояния ядер. Возбужденные состояния в ОМО возникают при переходе одного или нескольких нуклонов на более высокие одночастичные уровни. Наиболее просто выглядит спектр возбуждений ядер с одним нуклоном сверх заполненной подоболочки или с вакансией («дыркой») в последней. Нижние возбужденные состояния такого ядра получаются путем перемещения на более высокие подоболочки или «дырки» на нижние подоболочки, вглубь ядра. Здесь прослеживается аналогия с атомом, в котором возбужденные состояния есть результат перехода электронов на более высокие энергетические уровни. Однако, помимо одночастичных возбуждений, в ядре существуют коллективные возбуждения, которые не удается объяснить в рамках ОМО. В связи с этим атомное ядро по характеру своих возбуждений ближе к молекуле, где наряду с одноэлектронными переходами возможны и коллективные возбуждения – колебания и вращения. Идея о существовании у ядер коллективных вращательных и колебательных состояний оформилась к 50-м гг. XX в. из анализа схем уровней возбуждения четно-четных ядер. Для объяснения их многообразия была использована аналогия с молекулярной спектроскопией.
 Одночастичное возбуждение в молекуле – электронное. Два электронных состояния отличаются тем, какой из молекулярных орбиталей принадлежит внешний электрон. Разница в энергиях орбиталей – от 1 до ~10 эВ. В атомных ядрах энергии однонуклонных возбуждений измеряются единицами МэВ (разница между энергиями подоболочек). Коллективные возбуждения ядра требуют значительно меньших энергий.
Одночастичное возбуждение в молекуле – электронное. Два электронных состояния отличаются тем, какой из молекулярных орбиталей принадлежит внешний электрон. Разница в энергиях орбиталей – от 1 до ~10 эВ. В атомных ядрах энергии однонуклонных возбуждений измеряются единицами МэВ (разница между энергиями подоболочек). Коллективные возбуждения ядра требуют значительно меньших энергий.
а) Вращательный спектр. Система частиц, движущихся в сферически симметричном потенциальном поле, не может иметь вращательного спектра энергий.[35] Следовательно, сферическое ядро не имеет вращательных степеней свободы, а в случае несферического ядра в форме эллипсоида возможны лишь вращения вокруг осей x или y (см. рис. 4.4).[36] Для простоты рассмотрим четно-четное ядро, спин которого в основном состоянии равен нулю. Если такое ядро вращательно возбуждено, его спин полностью обусловлен вращением. Энергия вращательного движения
 , (4.10)
, (4.10)
где Ix – эффективный момент инерции,[37] J = 0, 1, 2 и т.д. – вращательное квантовое число. Для бесспинового ядра, имеющего форму эллипсоида вращения, возможны лишь четные значения J, поскольку при возбуждении вращений четность ядра должна сохраняться. Таким образом, характерными признаками вращательных уровней четно-четных ядер являются пропорциональность энергии возбуждения величине J(J + 1), а также последовательность спинов и четностей JP = 0+, 2+, 4+ и т.д. (рис. 4.5). Типичная энергия Е2вращательных возбуждений ядер – 10-100 кэВ. По мере приближения к магическим (сферическим) ядрам эффективный момент инерции уменьшается, и вращательные уровни уходят вверх по шкале энергии.
б) Колебательный спектр. Другие коллективные возбуждения ядра можно рассматривать уже с точки зрения капельной модели. Это, прежде всего, колебания поверхности ядра около равновесной формы (объемные колебания из-за несжимаемости ядерной материи практически невозможны). Два типа таких колебаний показаны на рис. 4.6. Самая низкоэнергетическая область спектра – это квадрупольные[38], затем октупольные[39] и т.д. колебания.
Если говорить об осцилляторе, совершающем гармонические колебания какой-либо определенной мультипольности L, т.е. квадрупольные (L = 2), октупольные (L = 3) и т.д., то по законам квантовой механики уровни энергии такого осциллятора даются выражением
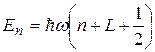 , (4.11)
, (4.11)
где колебательное квантовое число n = 0, 1, 2 и т.д. Таким образом, при L = const колебательный спектр эквидистантен; характерная величина ΔE = ћω составляет от 0,1 до 1 МэВ. Однако эквидистантные последовательности возбужденных уровней наблюдаются редко, так как при сильных колебаниях (большие n) нарушается их гармоничность. Возбуждение колебаний способно вызвать потерю устойчивости тяжелого ядра: оно может, например, разделиться на две части.
 Отметим, что в спектре поверхностных колебаний, в процессе которых протоны и нейтроны двигаются синхронно, отсутствуют дипольные (L = 1) колебания: при колебаниях такого типа ядро перемещается как единое целое без изменения своего внутреннего состояния (меняется лишь положение центра масс).
Отметим, что в спектре поверхностных колебаний, в процессе которых протоны и нейтроны двигаются синхронно, отсутствуют дипольные (L = 1) колебания: при колебаниях такого типа ядро перемещается как единое целое без изменения своего внутреннего состояния (меняется лишь положение центра масс).
Выше, говоря о коллективных возбуждениях, мы выделили лишь два крайних случая: несферические ядра, имеющие вращательные спектры, и сферические ядра, имеющие колебательные спектры. В общем случае наблюдается весьма непростая связь между этими двумя формами коллективных движений, вплоть до того что одно и то же ядро может иметь две равновесные формы и совершать между ними колебания (такие ядра называют мягкими).
Реальный ядерный спектр оказывается, таким образом, сложным. Он является наложением одно-, двух- (и т.д.) частичных и коллективных возбуждений. Лишь у очень ограниченного числа ядер доминирует какая-то одна ветвь возбуждения. С ростом энергии плотность состояний (т.е. число уровней, приходящееся на единичный интервал энергии) быстро растет. При энергии более 10 МэВ спектр возбуждений уже можно считать непрерывным, причем в возбуждение вовлекаются не только внешние, но и внутренние, то есть сильно связанные нуклоны. В результате спектр возбуждений существенно обогащается. При энергии возбуждения ~20 МэВ появляются т.н. поляризационные колебания. Их происхождение связано с тем, что ядро можно рассматривать как смесь двух несжимаемых нуклонных жидкостей (протонной и нейтронной), проникающих друг в друга. Поляризационные колебания представляют собой колебания капли одной жидкости относительно другой. На рис. 4.7 показаны три примера таких возбуждений – электрические дипольные (Е1), электрические квадрупольные (Е2) и магнитные дипольные (М1), называемые ножничными. Колебания Е1 являются наиболее мощным коллективным возбуждением. Они наблюдаются у всех ядер с А > 2 и называются гигантским дипольным резонансом.
Верхняя граница спектра ядерных возбуждений – около 100 МэВ. При более высоких энергиях, передаваемых ядру, начинается возбуждение самих нуклонов.

Дата добавления: 2015-05-26; просмотров: 2800;
