Закон Кирхгофа

Отношение излучательной способности тела к его поглощательной способности не зависит от природы тела, оно является для всех тел одной и той же функцией частоты и температуры, т.е.

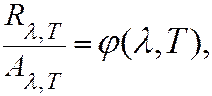(6.40.8)

где 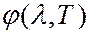- функция Кирхгофа, зависящая от длины волны и температуры. Для абсолютно черного тела 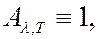поэтому из закона Кирхгофа (6.40.8) следует, что для абсолютно черного тела 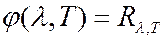, т.е. универсальная функция Кирхгофа представляет собой спектральную плотность излучательности абсолютно черного тела (в дальнейшем иногда спектральную плотность излучательности абсолютно черного тела – функцию Кирхгофа – будем обозначать 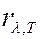, , 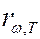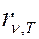или , ). 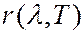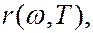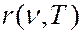У реальных тел спектральная поглощательная способность всегда меньше единицы ( 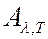< 1), поэтому спектральная плотность излучательности любого реального тела всегда меньше спектральной плотности излучательности абсолютно черного тела при тех же значениях 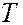и :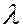

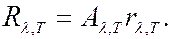(6.40.9)

Из закона Кирхгофа также следует, что если тело при данной температуре 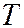не поглощает излучения в интервале длин волн от 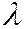до 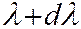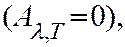то оно не может при температуре 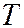излучать в этом же интервале длин волн:

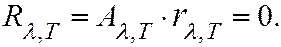(6.40.10)

Используя соотношение (6.40.9), выражению (6.40.6) для энергетической светимости тела можно придать вид

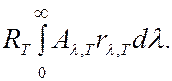(6.40.11)

На рисунке представлены экспериментальные кривые, выражающие зависимость спектральной плотности излучательности 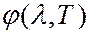абсолютно черного тела от длины волны 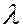для разных температур абсолютно черного тела. Площадь под кривой дает энергетическую светимость абсолютно черного тела при данной температуре. С ростом температуры энергетическая светимость сильно растет, а максимум кривой смещается в сторону более коротких длин волн.

6.6.4. Закон Стефана – Больцмана и законы Вина

На основе анализа экспериментальных данных физики предприняли ряд попыток получить теоретически вид функции 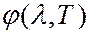. Исходя из термодинамических соображений, Стефан (1879 г.) и Больцман (1884 г.) получили для энергетической светимости абсолютно черного тела следующее соотношение:

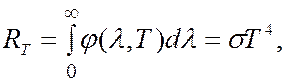(6.40.12)

где 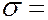5,7∙10^-8 Вт/(м²∙К⁴) – постоянная Стефана – Больцмана. Соотношение (6.40.12) между энергетической светимостью абсолютно черного тела и его температурой получило название закона Стефана – Больцмана: энергетическая светимость абсолютно черного тела пропорциональна четвертой степени его абсолютной температуры.

Воспользовавшись электромагнитной теорией, Вин (1893 г.) установил зависимость длины волны 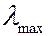, на которую приходится максимум функции 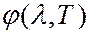_, от температуры:

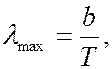(6.40.13)

где 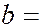2,9∙10^-3 м∙К. Соотношение (6.40.13) носит название закона смещения Вина:длина волны, на которую приходится максимум испускательной способности абсолютно черного тела, обратно пропорциональна абсолютной температуре. Закон смещения Вина объясняет, почему при понижении температуры нагретых тел в их спектре все сильнее преобладает длинноволновое излучение.

Второй закон Вина определяет зависимость максимального значения спектральной плотности излучательности 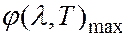от температуры:

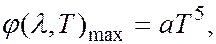(6.40.14)

где 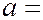1,29∙10^-5 Вт/м³∙К⁵.

6.6.5. Формулы Рэлея – Джинса и Планка

Д.Рэлей и Д.Джинс применили к тепловому излучению методы статистической физики и закон равнораспределения энергии по степеням свободы. Формула Рэлея – Джинса для спектральной плотности излучательности абсолютно черного тела имеет вид:

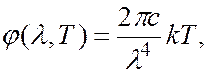(6.40.15)

где 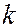– постоянная Больцмана. В зависимости от частоты 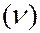выражение для спектральной плотности излучательности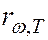 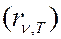абсолютно черного тела принимает вид:

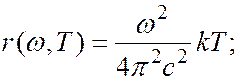(6.40.16)

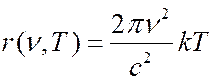. (6.40.17)

Формула Рэлея – Джинса хорошо согласуется с экспериментальными данными только в области длинных волн (малых частот) и больших температур. В области коротких волн она расходится с экспериментом.

Интегри рование выражения (6.40.12) с учетом (6.40.15) дает для энергетической светимости 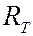бесконечно большое значение, что противоречит закону Стефана – Больцмана. Этот результат получил название «ультрафиолетовой катастрофы». На рисунке приведено сравнение экспериментальной зависимости с кривой, пстроенной по формуле Рэлея – Джинса.

В 1900 г. М.Планк нашел вид функци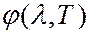и или 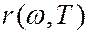. Он сделал предположение противоречащее классическим представлениям: предположил, что электромагнитное излучение испускается не непрерывно, а в виде отдельных порций энергии 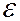(квантов), величина которых пропорциональна частоте излучения:

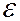
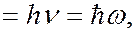(6.40.18)

где 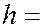6.62∙10^-34 Дж∙с и 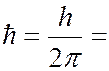1,054∙10^-34 Дж∙с – постоянные Планка. (Постоянную Планка иногда называют квантом действия). Тогда энергия 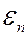, излучаемая на частоте , должна быть кратна величине (6.40.18):

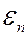
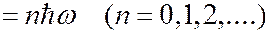. (6.40.19)

Согласно распределению Больцмана вероятность 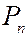, того, что энергия излучения имеет величину 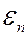, равна:

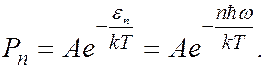(6.40.20)

Используя вероятностный подход, М.Планк для спектральной плотности излучательности абсолютно черного тела получил следующие формулы:

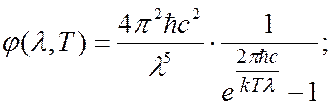(6.40.21)

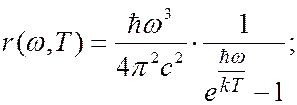(6.40.22)

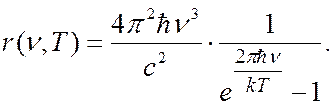(6.40.23)

Формулы Планка точно согласуются с экспериментом во всем итервале частот от 0 до 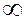(соответственно, во всем итервале длин волн). В случае малых частот (больших длин волн), когда 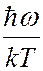<< 1, формула Планка переходит в формулу Рэлея – Джинса. Если в формулу (6.40.12) для энергетической светимости абсолютно черного тела подставить выражение (6.40.21), то получим закон Стефана – Больцмана:

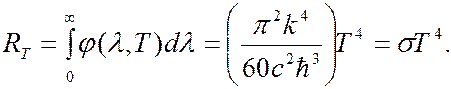(6.40.24)

Из соотношения (6.40.24) получается значение постоянной Стефана - Больцмана, хорошо согласующееся с экспериментальным значением. Дифференцируя выражение (6.40.21) по 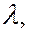можно получить значение постоянной 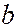в законе смещения Вина (6.40.13), совпадающее с экспериментальным значением:

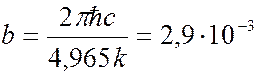м∙К. (6.40.25)

Контрольные вопросы для самоподготовки студентов:

1. Что называется излучательностью тела, спектральной плотностью излучательности, спектральной поглощательной способностью?

2. Сформулируйте закон Кирхгофа.

3. Какое тело называют абсолютно черным?

5. Формулы Релея-Джинса и Планка.

Литературные источники:

1. Трофимова, Т.И. Курс физики: учеб. пособие для вузов / Т.И. Трофимова. – М.: ACADEMIA, 2008.

2. Савельев, И.В. Курс общей физики: учеб. пособие для втузов: в 3-х томах / И.В.Савельев. – СПб.: Спец. лит., 2005.