От тонких пластинок и пленок
При падении световой волны на тонкую прозрачную пластинку или пленку происходит отражение от верхней и нижней поверхностей пластинки. При этом возникают когерентные световые волны, которые могут интерферировать. Пусть на плоскопараллельную пластинку с показателем преломления 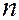 и толщиной
и толщиной 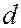 под углом
под углом 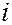 падает плоская монохроматическая волна. Пластинка отбрасывает вверх два когерентных
падает плоская монохроматическая волна. Пластинка отбрасывает вверх два когерентных 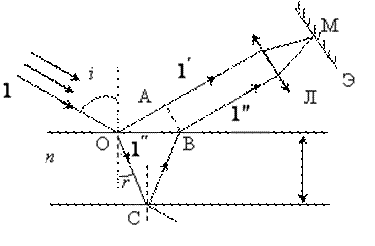 параллельных луча света 1' и 1'', из которых первый образуется за счет отражения от верхней поверхности пластинки в точке О, второй – вследствие отражения от нижней поверхности в точке С. Проведем перпендикулярную к отраженным лучам плоскость AB. является фронтом волны. На пути от этой плоскости до точки наблюдения разность фаз не изменяется. До этой плоскости проходят различные пути, поэтому оптическая разность хода лучей 1' и 1'' будет равна
параллельных луча света 1' и 1'', из которых первый образуется за счет отражения от верхней поверхности пластинки в точке О, второй – вследствие отражения от нижней поверхности в точке С. Проведем перпендикулярную к отраженным лучам плоскость AB. является фронтом волны. На пути от этой плоскости до точки наблюдения разность фаз не изменяется. До этой плоскости проходят различные пути, поэтому оптическая разность хода лучей 1' и 1'' будет равна
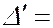
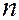 (ОС+СВ) – ОА.
(ОС+СВ) – ОА.
Учитывая геометрические соотношения и закон преломления, это выражение можно привести к виду:
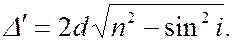 (6.36.12)
(6.36.12)
При вычислении разности фаз между колебаниями лучей 1' и 1'', кроме оптической разности хода 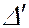 , необходимо учесть разные условия отражения световой волны от верхней и нижней поверхностей пластинки. При отражении световой волны от границы раздела среды оптически менее плотной со средой оптически более плотной (в точке О) фаза колебаний светового вектора изменяется на
, необходимо учесть разные условия отражения световой волны от верхней и нижней поверхностей пластинки. При отражении световой волны от границы раздела среды оптически менее плотной со средой оптически более плотной (в точке О) фаза колебаний светового вектора изменяется на 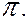 При отражении от границы раздела среды оптически более плотной со средой оптически менее плотной (точка С) изменения фазы не происходит. По этой причине между лучами 1' и 1'' возникает дополнительная разность фаз, равная
При отражении от границы раздела среды оптически более плотной со средой оптически менее плотной (точка С) изменения фазы не происходит. По этой причине между лучами 1' и 1'' возникает дополнительная разность фаз, равная 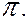 Ее учитывают, добавляя к
Ее учитывают, добавляя к 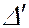 (или вычитая из нее) половину длины волны. С учетом этого, результирующая оптическая разность хода равна:
(или вычитая из нее) половину длины волны. С учетом этого, результирующая оптическая разность хода равна:
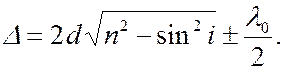 (6.36.13)
(6.36.13)
Собирающая линза фокусирует параллельные лучи в одной из точек фокальной плоскости на экране, где они будут интерферировать.
Условие максимума:
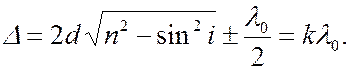 (6.36.14)
(6.36.14)
Условие минимума:
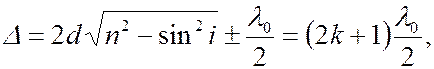 (6.36.15)
(6.36.15)
где  0, 1, 2, …. – порядок интерференционного максимума. Возможные значения
0, 1, 2, …. – порядок интерференционного максимума. Возможные значения 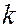 для данной пластинки зависят от угла падения
для данной пластинки зависят от угла падения 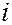 .
.
Дата добавления: 2015-05-26; просмотров: 880;
