Интерференция света в тонких пленках
В природе часто можно наблюдать окрашивание тонких пленок (масляные пленки на воде, мыльные пузыри, оксидные пленки на металлах), возникающие в результате интерференции света, отраженного двумя поверхностями пленки.
Пластинка постоянной толщины. При падении световой волны на тонкую прозрачную пластинку (или пленку) происходит отражение от обеих поверхностей пластинки. В результате возникают две световые волны, которые при определенных условиях могут интерферировать.
 |
Пусть на прозрачную плоскопараллельную пластинку с показателем преломления п падает плоская световая волна (параллельный пучок света) (рис.18.5.).
В результате отражений от поверхностей пластинки, часть света возвращается в исходную среду. Отраженный свет состоит из лучей, испытавших одно-, трех-, пяти- и т.д. кратное отражение. Ввиду малой интенсивности лучи трехкратного отражения и выше принимать в расчет не будем (при n=1,5 от поверхности пластинки отражается примерно 4 % падающего светового потока). Однократно отраженные от пластинки лучи 1 и 2 когерентны, если оптическая разность их хода меньше длины когерентности падающей волны. Если на пути лучей поставить собирающую линзу, то на экране, совмещенном с фокальной плоскостью линзы, возникнет интерференционная картина. Роль линзы может играть хрусталик, а экрана - сетчатка глаза. В этом случае глаз должен быть аккомодирован (наведен на резкость) на бесконечность.
Оптическая разность хода, возникающая между двумя интерферирующими лучами от точки O до точки P
.
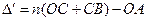Согласно рисунку (18.5)
, 
.
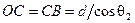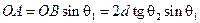Учитывая закон преломления
,
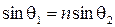получим
.
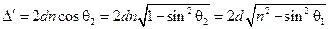При вычислении разности колебаний в лучах 1 и 2 нужно, кроме оптической разности хода D¢, учесть возможность изменения фазы волны при отражении. В точке O отражение происходит от оптически более плотной среды. Поэтому фаза отраженной волны изменяется на p (для определенности считаем, что происходит потеря полуволны). В точке C отражение происходит от оптически менее плотной среды, так что скачка фазы не происходит. С учетом потери полуволны для оптической разности хода получим
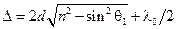. (18.3.1)
В точке P будет интерференционный максимум, если
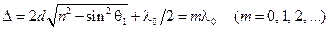, (18.3.2.,а)
и минимум, если
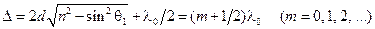. (18.3.2.,б)
Выясним условия, при которых эти волны окажутся когерентными и смогут интерферировать. Для того, чтобы имела место временная когерентность, разность хода (18.3.1) не должна превышать длину когерентности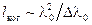 
. Следовательно, должно выполнятся условие
.
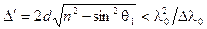В рассеянном свете имеются лучи самых разнообразных направлений. Лучи, параллельные некоторому направлению, после отражения соберутся в одной точке и создадут в ней освещенность, определяемую значением оптической разности хода. Лучи, идущие в другом направлении, соберутся в другой точке и т.д. В результате возникает система чередующихся светлых и темных полос (если линза параллельна пластинке, полосы имеет вид концентрических колец с центром в фокусе линзы). Каждая полоса образована лучами, падающими на пластинку под одинаковым углом. Поэтому получающиеся интерференционные полосы носят название полос равного наклона.
Согласно формуле (18.3.2.,а) положение максимумов зависит от длины волны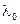 
. Поэтому в белом свете интерференционная картина приобретает радужную окраску. Возможность наблюдения интерференционной картины в белом свете определяется способностью глаза различать оттенки цвета.
Кольца Ньютона. Классическим примером полос равной толщины являются кольца Ньютона. Они наблюдаются при отражении света от соприкасающихся друг с другом толстой плоскопараллельной стеклянной пластинки и плоско-выпуклой линзы с большим радиусом кривизны (рис.18.6.).
 |
Роль тонкой пленки, от поверхностей которой отражаются когерентные волны, играет воздушный зазор между пластинками и линзой (вследствие большой толщины пластинки и линзы, отраженные от других поверхностей лучи в образовании интерференционной картины не участвуют). При нормальном падении света полосы равной толщины имеют вид концентрических окружностей, при наклонном падении – эллипсов. Найдем радиусы колец Ньютона, получающихся при падении света по нормали к пластинке. Из рис. 18.6. следует, что
,
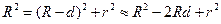где R – радиус кривизны линзы, r – радиус окружности, которой соответствует зазор толщины d. Таким образом,
.
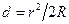С учетом потери полуволны, возникающей при отражении от пластинки, оптическая разность хода лучей равна
.
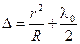Используя условия максимума (18.3.2.,а) и минимума (18.3.2.,б), получим выражения для радиусов m-го светлого и m-го темного кольца соответственно
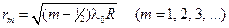, (18.3.4.,а)
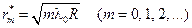. (18.3.4.,б)
Дата добавления: 2015-04-19; просмотров: 1863;