Поперечный и продольный профили реки.

Русло реки Размеры и форма русла сильно меняются по длине реки в зависимости от водности реки, строения долины, характера пород, слагающих русло. Морфологические особенности русла могут быть охарактиризованы при помощи плана русла с нанесенными на нем изобатами, или горизонталями, и поперечного профиля русла.

Сечение русла вертикальной плоскостью, перпендикулярной к направлению течения, называется водным сечением потока. Часть площади водного сечения, где наблюдаются скорости течения, называется площадью живого сечения. Та же часть площади водного сечения, где скорости течения практически отсутствуют, называется площадью мертвого пространства.

В живом сечении потока различают площадь живого сечения ω (км²) и смоченный периметр χ(м), представляющий собой длину линии, ограничивающей смоченную часть живого сечения. Отношение величины площади живого сечения к смоченному периметру называется гидравлическим радиусом R.Таким образом, R = ω / χ.Отношение величины площади живого сечения к ширине реки Bназывается средней глубиной h живого сечения, или h = ω/B.

Элементы живого сечения - площадь его, гидравлический радиус, средняя глубина – не остаются постояннымы. Величины их находятся в прямой зависимости от уровней воды в реке: с повышением уровней они увеличиваются, с понижением уменьшаются .

Продольный прфиль реки.Продольный профиль рек характеризуется продольным профилем речной долины и продольным профилем водной поверхности.Разность высот Dh двух каких-либо точек водной поверхности по длине реки называется падением ее. Отношение величины падения к длине данного участка L называется уклоном i реки. Таким образом , i = Dh/L. Падение выражается обычно в метрах на 1 км ; уклон же представляет собой величину безразмерную и выражается в виде десятичной дроби или промилле (в сантиметрах на 1 км).

Продольный профиль реки характеризует изменение по длине потока отметок дна и свободной поверхности воды. Линия дна по продольном профиле всегда волнистая вследствие чередования глубоких и мелких мест в русле реки. Линия же продольного профиля водной поверхности носит сравнительно плавный характер. При вычерчивании продольного профиля вертикальный и горизонтальный масштаб даются разные, так как разность высот истока и устья во много раз меньше длины реки.

Обычно продольные профили строят по линии наибольших глубин. На продольном профиле показывают: линию дна реки по фарватеру; меженный уровень воды; максимальный уровень воды; линии правого и левого берегов; перекаты (перевалы), пороги, места впадения притоков; водомерные посты, реперы, мосты, плотины.

Для общей оценки уклона реки введено понятие «среднего взвешенного уклона» I (%о), представляющего собой условный выравненный уклон ломаного профиля, эквивалентный сумме частных средних уклонов продольного профиля водотока.

LgI = Σ ( l_i /L) lgI _i ,

где, l_i –частных участков продольного профиля между точками перегибов, км; L – гидрографическая длина водотока до пункта наблюдений, км; I _i– частные средние уклоны отдельных участков продольного профиля водотока, %о.

Профили отдельных рек, естественно, носят различный характер в зависимости от уклона долины, литологического состава пород в русле и на водосборе, гидологическог режима стока воды и наносов, положения русла в плане и других факторов.

Установлены следующие типы продольных профилей дна рек:

1. Вогнутый с уменьшением уклона дна от истока к устью реки.

2. Прямолинейный , наблюдающийся чаще всего у малых рек.

3. Выпуклый при увеличении уклона дна от истока к устью реки.

Перестройка продольного профиля в большинстве случаев сопровождается глубинной и плановой (боковой ) эрозией.

Поперечный профиль реки. Форма поперечных профилей рек отличается большим разнообразием. Так, на искривленных участках профиль дна реки асимметричный . Вертикаль с большей глубиной смещена ближе к вогнутому берегу. Линия поверхности воды в поперечном сечении имеет наклон, кроме очень редких случаев, когда на криволинейных участках реки центробежная сила и отклоняющая сила вращения Земли при алгебраическом сложении дают нуль. Форма поперечных сечений может быть схематизирована в виде параболы. Для русл с поймами возможна схематизация в виде параболического русла и горизонтальной симметричной или несимметричной поймы.

На поперечном профиле показывют: дно или ложе – самая низкая часть на поперочном профиле (подводная часть русла); уреза воды (правый и левый) – линия пересечения поверхности воды в русле с берегом ( глубина воды равна нулю); берег-надводная часть русла (правый и левый ) выше уреза воды; бровка – линия сопряжения берега с дном русла; глубина русла (h) – расстоянние по вертикали от дна до уровня воды; высота берега – превышение его бровки над урезом воды; ширина русла (L) – расстояние между бровками берегов.

Поперечный профиль водной поверхности реки. Поперечный профиль водной поверхности реки, вообще говоря, не представляет собой горизонтальную линию. Он характеризуется, с одной стороны, наличием превышения уровня воды у одного берега над уровнем у другого, а с другой - в ряде случаев представляет собой довольно сложные кривые линии.

Причины, вызывающие разность в уровнях у противоположных берегов, заключаются в следующем. Русло реки никогда не бывает прямолинейным. При движении воды на участке с закруглением развивается центробежная сила. Степень кривизны русла характеризуется так называемым радиусом кривизны, представляющим собой радиус окружности дуга которой совпадает с кривой, изображающей очертания русла на данном участке. Центр окружности называется центром кривизны. Каждая частица воды, движущаяся на закруглении, испытывает действие центробежной силы, направленной по радиусу кривизны (рис.7).

Величина этой силы

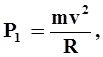
(1)

где m - масса частицы; v - продольная скорость движения частицы; R - радиус кривизны. На рис 7а эта сила изображена в виде вектора, направленного в сторону вогнутого берега. Под действием этой силы частица будет устремляться к вогнутому берегу.

Каждая частица, кроме того, находится под действием силы тяжести f , изображенной на рис. 7б в виде вектора, направленного сверху вниз по вертикали. На этом же рисунке сила Р₁ изображена в виде горизонтальной линии.

Равнодействующая обеих сил Р образует некоторый угол a с вертикально направленным вектором, изображающим силу f.

Известно, что уровенная поверхность всегда нормальна к равнодействующей всех сил, направленных на нее. Таким образом, уровенная поверхность под действием обеих сил - центробежной Р₁ и силы тяжестиf- займет положение ДЕ, составляющее угол a, равный углу между силами Р и f, так как стороны углов fМР и ЕМВ взаимно-перпендикулярны. Известно, что сила тяжести f = mg, где m - масса частицы; g - ускорение силы тяжести. Из треугольника fМР видно, что tga = Р₁ : 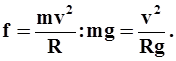Так как угол a обычно невелик, то можно принять sinaравным tga. 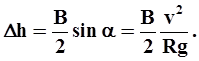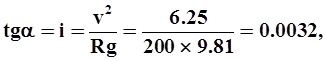Из треугольника ЕМВ следует, что Так например, если V= 2.5 м/c, B = 200 м, R=200 м, то а следовательно, 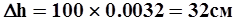т.е уровень воды у вогнутого берега на 32 см выше, чем у выпуклого.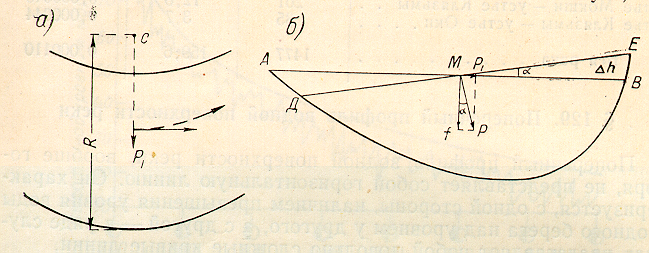

Рис. 7. Действие центробежной силы на водную поверхность на изгибе.

а - план участка, б - живое сечение.

Другая причина, вызывающая разность уровней у противоположных берегов. - сила Кориолиса. Известно, что под действием вращения Земли вокруг оси все движущиеся тела отклоняются от первоначального направления движения в северном полушарии вправо, в южном - влево. Величина силы Кориолиса

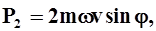(2)

где m - масса частицы; w - угловая скорость суточного вращения Земли; j - широта места. Подобно тому, как и в предыдущем случае, равнодействующая двух сил - силы тяжести и Кориолиса Р₂ будет составлять некоторый угол с направлением силы тяжести, следовательно, и поверхность воды составит такой же угол с горизонтальной плоскостью. Отсюда поперечный уклон, вызванный действием силы Кориолиса, будет равен

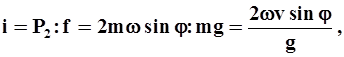или, так как 2 w = 0.0001458,

.

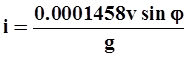Для случая , рассмотренного ранее, т.е. для реки со скоростью течения V=2.5 м/cекпри ширине реки 200 ми для j = 55⁰ , поперечный уклон i= 0.000030, а превышение уровня воды у правого берега над уровнем у левогоDh = 0.003 м, или 0.3 см.

В тех случаях, когда направление силы Кориолиса совпадает с направлением центробежной силы потока на закруглениях, равнодействующая этих сил будет равна их сумме, т.е. Р₁ +Р₂ , при противоположных направлениях этих сил равнодействующая будет равна их разности т.е. Р₁ -Р_2.