Систематическая и случайная вариация
Причины вариации могут быть различными. С точки зрения определенного исследования все причины вариации можно разделить на две группы: систематические (постоянные) и случайные причины. Так для вариации заработной платы работников бригады в качестве систематической причины выступает, вероятно, уровень квалификации, разряд работников. Все остальные причины различий в заработной плате можно рассматривать как случайные. Важно отметить, что деление причин вариации на систематические и случайные во многом определяется характером и целью исследования. например, при изучении зависимости уровня заработной платы от профессии работника в качестве систематической причины вариации заработной платы следует рассматривать профессиональную принадлежность.
Вариация, обусловленная систематическими, постоянными причинами, называется систематической или факторной вариацией. Она оценивается с помощью показателей систематической (или факторной, межгрупповой) дисперсии и обозначается 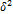 (дельта).
(дельта).
Вариация, обусловленная случайными причинами, называется случайной или остаточной вариацией, ее дисперсия обозначается 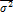 .
.
Для определения систематической и случайной вариации пользуются аналитической группировкой, произведенной по факторному признаку. Вариация результативного признака, обусловленная фактором, положенным в основание группировки, является факторной (межгрупповой) вариацией. Систематическая дисперсия рассчитывается по формуле:
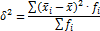
где 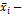 среднее значение результативного признака в i-той группе.
среднее значение результативного признака в i-той группе.
Случайная дисперсия определяется как средняя арифметическая внутригрупповых дисперсий:
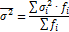
где 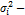 дисперсия результативного признака в i-той группе.
дисперсия результативного признака в i-той группе.
В математической статистике доказано, что сумма систематической и случайно дисперсий равна общей дисперсии исследуемого признака (правило сложения дисперсий):
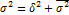
Правило сложения дисперсий имеет большое значение для статистического анализа. На его основе можно оценить наличие или отсутствие, а также тесноту связи между факторным и результативным признаками. Для характеристики тесноты связи между результативным и факторным признаками межгрупповую дисперсию сопоставляют с общей дисперсией. Отношение межгрупповой дисперсии к общей дисперсии называется корреляционным отношением и обозначается 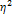 (эта):
(эта):
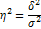
Данное соотношение характеризует удельный вес систематической дисперсии в общей дисперсии. Иными словами, корреляционное отношение характеризует удельный вес вариации, обусловленной факторами, положенными в основу аналитической группировки, в общей вариации результативного признака. Если значение корреляционного отношения равно 0, то связь между изучаемыми признаками отсутствует. Максимально возможное значение корреляционного отношения равно 1. В этом случае между факторным и результативным признаками существует функциональная связь. Чем больше значение 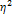 , тем сильнее влияние на результативный признак факторных признаков, положенных в основу аналитической группировки.
, тем сильнее влияние на результативный признак факторных признаков, положенных в основу аналитической группировки.
Для измерения вариации в статистике используются показатели: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации.
Наиболее простым показателем, характеризующим размер вариации, является размах вариации. Размах вариации (R) – это разность между максимальным и минимальным значением признака в данной совокупности.
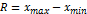
Размах вариации позволяет оценить границы изменения признака в совокупности. В то же время с помощью данного показателя нельзя измерить колеблемость признака внутри этих границ. Так, если по результатом сессии в академической группе все студенты, за исключением одного, получили 5 на экзамене по статистике, а 1 студент – 2 балла, то размах вариации составляет максимальную величину для экзаменационных оценок: R=5-2=3. На самом же деле степень колеблемости этого признака в данной совокупности невелика, а «двойка» является нехарактерным для группы значением признака, нехарактерной оценкой. Размах вариации не позволяет оценить варьирование признака внутри верхней и нижней границ. Избежать такого недостатка в измерении вариации позволяют другие показатели.
Среднее линейное отклонение (  ) – характеризует средний размер абсолютных отклонений индивидуальных значений признаков от средней величины.
) – характеризует средний размер абсолютных отклонений индивидуальных значений признаков от средней величины.
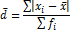
Отклонения от средней данной формуле представлены без учета знака «плюс» или «минус», так 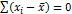 , что является свойством средней арифметической. Среднее линейное отклонение обобщает все отклонения изучаемого признака от средней величины. Среднее линейное отклонение является именованным числом, оно выражено в тех же единицах, что и значения признака.
, что является свойством средней арифметической. Среднее линейное отклонение обобщает все отклонения изучаемого признака от средней величины. Среднее линейное отклонение является именованным числом, оно выражено в тех же единицах, что и значения признака.
Среднее линейное отклонение и размах вариации являются наиболее наглядными и простейшими оценками вариации. Но кроме них, для измерения вариации применяются дисперсия и среднее квадратическое отклонение.
Дисперсия – средний квадрат отклонений индивидуальных значений признака от средней величины. Дисперсия обозначается греческой буквой 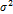 (сигма) в квадрате. Дисперсия является безмерной величиной. Так же, как и средняя величина, дисперсия может быть рассчитана по простой и взвешенной формулам. Формула простого среднего квадрат отклонений:
(сигма) в квадрате. Дисперсия является безмерной величиной. Так же, как и средняя величина, дисперсия может быть рассчитана по простой и взвешенной формулам. Формула простого среднего квадрат отклонений:
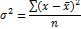
Для сгруппированных данных используется взвешенная формула дисперсии:
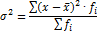
В некоторых статистических исследованиях необходимо оценить вариацию альтернативного признака, то есть признака, принимающего только два возможных значения. К примеру, в группе из 20 студентов 15 человек сдали экзамен, а 5 – не сдали. Альтернативный признак – положительный или отрицательный результат на экзамене. Среднее значение альтернативного признака определяется как доля единиц совокупности, обладающих определенным значением признака, например, положительным результатом на экзамене. То есть, 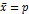 , где
, где 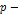 доля единиц, обладающих признаком. В нашем примере p=15:20=0,75. Дисперсия альтернативного признака рассчитывается по формуле:
доля единиц, обладающих признаком. В нашем примере p=15:20=0,75. Дисперсия альтернативного признака рассчитывается по формуле:
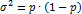
Таким образом, 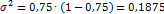
Показатель дисперсии широко используется в различного рода статистических исследованиях, финансовых расчетах, в статистическом прогнозировании.
Для измерения вариации наряду с дисперсией широко используется среднее квадратическое отклонение (СКО) или стандартное отклонение. Среднее квадратическое отклонение (  ) определяется как квадратный корень из дисперсии. Этот показатель является размерной величиной и имеет размерность изучаемого признака. Формула:
) определяется как квадратный корень из дисперсии. Этот показатель является размерной величиной и имеет размерность изучаемого признака. Формула:
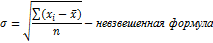
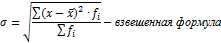
Смысловое содержание СКО такое же, как и среднего линейного отклонения. Чем меньше значение СКО при прочих равных условиях, тем ниже вариация изучаемого признака, и следовательно, выше однородность совокупности и типичнее средняя.
Рассмотренные показатели характеризуют абсолютное значение вариации и не позволяют оценить ее относительную значимость: их нельзя использовать для сравнения вариации в различных статистических совокупностях, имеющих разные средние величины, а тем более – для сравнения вариации различных признаков в одной совокупности. К примеру, с помощью этих показателей нельзя сопоставить размер вариации роста (в см) и веса (в кг) студентов группы или вариацию обеспеченности предприятий основными производственными фондами с вариацией объемов производства. Для сравнения вариации и оценки ее значимости используется коэффициент вариации.
Коэффициент вариации (V) – является относительным показателем вариации и рассчитывается путем сопоставления среднего отклонения со средним уровнем явления и измеряется, как правило, в процентах. Для расчета коэффициента вариации могут использоваться как среднее линейное отклонение, так и среднее квадратическое отклонение:

Если коэффициент вариации не превышает 33 %, то совокупность можно считать однородной по рассматриваемому признаку.
3.Стоимость капитала: содержание и значение. Этапы определения стоимости капитала. Стоимость заемного капитала.
Стоимость капитала: содержание и значение
Определение с позиции управления капиталом:
Стоимость капитала–затраты на привлечение единицы капитала. Это характеристика расходов, которые предприятие должно выплачивать за использование того или иного источника финансирования. Сумма выплат рассчитывается по величине чистой прибыли и определяется в процентах.
Пример:
Если предприятие должно выплачивать из чистой прибыли 40 тыс. руб. в год за использование 200 тыс. руб. каких-либо финансовых ресурсов, то цена данного источника равна: 40/200 = 0,2 = 20 %. Это определение с точки зрения управления источниками финансирования.
Определение с позиции управления инвестициями
Стоимость капитала - уровень доходности инвестиций, при котором стоимость акций остается неизменной.
Стоимость капитала - минимальный уровень доходности инвестиций на вложенный капитал, необходимый для поддержания рыночной стоимости акций. Данная трактовка дана с позиций управления инвестициями (активами).
Требование
Для нормального функционирования предприятия в долгосрочной перспективе необходимо, чтобы отдача от используемого капитала была больше, чем затраты на привлечение капитала.
Этапы определения стоимости капитала
Определение стоимости капитала предприятия проводится в четыре этапа.
На первом этапе осуществляется идентификация основных компонентов, являющихся источниками формирования капитала фирмы.
На втором – рассчитывается цена каждого источника в отдельности.
На третьем этапе определяется средневзвешенная цена капитала на основании использования удельного веса каждого компонента в общей сумме инвестированного капитала.
В заключение (четвертый этап) разрабатываются мероприятия по оптимизации структуры капитала фирмы по различным критериям и формированию целевой структуры капитала.
Стоимость обязательств (долга)
Стоимость долга - стоимость заемных источников финансирования.
Эти источники также весьма отличаются друг от друга по параметрам, определяющим стоимость капитала. Различным образом оценивается стоимость кредитов и займов, с одной стороны, и кредиторской задолженности, с другой стороны.
Кредиторская задолженность:
| Зарубежная практика | Россия |
| КЗ=0 – все погашается в оговоренный контрактами срок, возникновение неплатежей по отдельным предприятиям быстро завершается процедурой банкротства. | КЗ>0 – кредиторская задолженность (краткосрочные пассивы) – важнейший источник финансирования, особенно в условиях неплатежей. КЗ сильно влияет на среднюю цену капитала, поэтому кредиторскую задолженность необходимо учитывать при оценке цены заемного капитала. Просроченная кредиторская задолженность ведет к пеням и штрафам |
Цена кредиторской задолженности определяется природой выплат по каждой статье кредиторской задолженности, поэтому необходимо рассматривать каждую крупную статью кредиторской задолженности отдельно.
| Цена кредиторской задолженности поставщикам | |
| Прямой способ | Косвенный способ |
| штрафы и пени, которые предприятие должно заплатить при задержке платежей. В ряде случаев платежи привязываются к курсу твердой валюты, тогда ценой задолженности будет увеличение курса валюты | Оценка потерь, вызванных неплатежами поставщикам: - судебные издержки; - потеря репутации; - рост цен на материалы; - перебои в снабжении. Данные потери не всегда поддаются количественной оценке. |
| Цена кредиторской задолженности перед бюджетом и задолженности внебюджетным фондам | |
| изменяется с принятием новых законодательных актов, уменьшением инфляции и изменением политики возврата долгов органами власти и внебюджетными фондами с приоритетом на получение текущей оплаты |
4.Задача: Рассчитайте на отчетный период количество денег, необходимых в качестве средства обращения и платежа по следующим данным:
1.Объемы и цены реализуемых товаров:
| Показатели | Виды товаров | |||
| А | В | С | Д | |
| - объем реализации товаров, шт. | ||||
| - цена за единицу товара, ден. ед./шт. | ||||
| - удельный вес товаров, проданных в кредит, % | - | - |
2.Стоимость оказанных услуг - 25 000 ден. ед.
3.Сумма взаимопогашающихся платежей - 28 000 ден. ед.
4.Сумма платежей по долговым обязательствам - 18 000 ден. ед.
5. Число оборотов денег равно 3.
Дата добавления: 2015-05-21; просмотров: 5017;
