Расчет скорости осаждения капель при известном их диаметре

Область ламинарного режима осаждения характеризуется следующими значениями параметра Рейнольдса:

10^(-4) < Re ≤ 2. (5.23)

Соответственно коэффициент гидравлического сопротивления среды движению капли при этом режиме равен:

ζ_о = 24 / Re. (5.24)

Из (5.4) с учетом (5.24) следует:

Re = Ar / 18. (5.25)

Используя граничные значения критерия Рейнольдса, из (5.23) по (5.25) легко рассчитать граничные значения критерия Архимеда в области ламинарного режима осаждения капель:

18∙10^(-6) < Ar ≤ 36 (5.26)

В области переходного режима осаждения:

2 < Re ≤ 500, (5.27)

а коэффициент гидравлического сопротивления среды осаждению капли определяют по формуле Алена:

ζ_о = 18,5 / Re^0,6. (5.28)

Из (5.4) с учетом (5.28) для критерия Рейнольдса получается:

Re = Ar^0,714 / 6,545. (5.29)

По аналогии с выводом (5.26) из (5.29) с учетом граничных значений критерия Re (5.27) следует, что соответствующие граничные значения критерия Архимеда в области переходного режима осаждения капель будут:

36 < Ar ≤ 83,3∙10³. (5.30)

Так как критерий Рейнольдса:

Re = ω_o∙d∙ρ_c / μ, (5.31)

то при известном диаметре частицы и значении Re (5.31) следует:

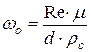. (5.32)

Таким образом, в области ламинарного режима скорость осаждения частицы равна:

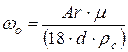. (5.33)

в области переходного режима осаждения:

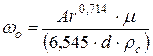. (5.34)

Итак для расчета скорости свободного осаждения капель при известном их диаметре, вначале рассчитывают критерий Архимеда:

Ar = d³∙ρ_c∙(ρ_д - ρ_с) g / μ² (5.35)

а, если его значение удовлетворяет неравенствам (5.26), то скорость считают по (5.32), а если - соответственно неравенствам (5.30), то по (5.34).