Числовые характеристики непрерывных случайных величин.

Определение. Математическое ожидание непрерывной случайной величины, имеющей функцию плотности распределения вероятностей 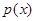, вычисляется по формуле:

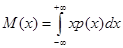. (17.1)

Определение. Дисперсиянепрерывной случайной величины определяется равенством

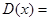
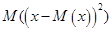
. (17.2)

Определение. Cреднее квадратическое отклонение: .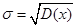

Как и в дискретном случае, математическое ожидание характеризует среднее значение случайной величины (ожидаемое значение), а дисперсияхарактеризует отклонение случайной величины 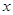от математического ожидания, т.е. разброс случайной величины относительно ее среднего значения.

На практике дисперсию (как и в случае дискретной случайной величины) удобно вычислять по формуле:

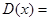
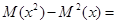
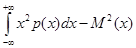. (17.3)

Рассмотрим теперь основные (наиболее распространенные) законы распределения непрерывных случайных величин.