Нормальное распределение непрерывных случайных величин.

Случайная величина 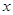называется распределенной по нормальному (Гауссовскому) закону с параметрами аи 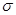( 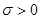), если плотность распределения вероятностей имеет вид

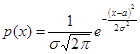, (19.1)

где .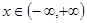

Величина, распределенная по нормальному закону, всегда имеет бесчисленное множество возможных значений, поэтому ее удобно изображать графически, с помощью графика плотности распределения. Согласно формуле

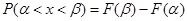
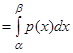
вероятность того, что случайная величина примет значение из интервала 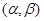равна площади под графиком функции 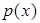на этом интервале (геометрический смысл определенного интеграла). Рассматриваемая функция 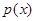неотрицательна и непрерывна. График функ­ции 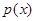имеет вид колокола и называется кривой Гаусса или нормальной кривой.

На рисунке изображено несколько кривых плотности распределения случайной величины, заданной по нормальному закону.

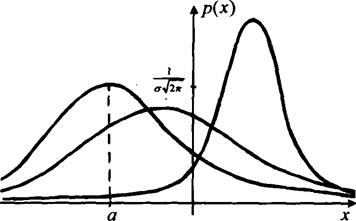
Все кривые имеют одну точку максимума, при удалении от которой вправо и влево кривые убывают. Максимум 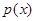достигается при 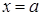и равен .

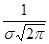Кривые симметричны относительно вертикальной прямой, проведенной через наивысшую точку. Площадь подграфика каждой кривой равна 1.

Различие отдельных кривых распределения состоит лишь в том, что суммарная площадь подграфика, одна и та же для всех кривых, различным образом распределена между различными участками. Основная часть площади подграфика любой кривой сосредоточена в непосредственной близости наивероятнейшего значения 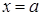, а это значение у всех трех кривых разное. При различных значениях 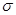и а получаются различные нормальные законы и различные графики плотности функции распределения.

Теоретические исследования показали, что большинство встречающихся на практике случайных величин имеет нормальный закон распределения. По этому закону распределяется скорость газовых молекул, вес новорожденных, размер одежды и обуви населения страны и много других случайных событий физической и биологической природы. Впервые эту закономерность заметил и теоретически обосновал А. Муавр.

При 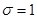, 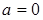функция 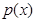совпадает с функцией 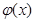, о которой уже шла речь в локальной предельной теореме Муавра–Лапласа. Плотность вероятности нормального распределения 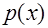легковыражается через :

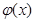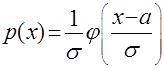
При таких значениях параметров нормальный закон называется основным.

Функция распределения для нормированной плотности называется функцией Лапласа и обозначается Φ(х). Мы также уже встречались с этой функцией.

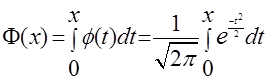
Функция Лапласа не зависит от конкретных параметров а и σ. Для функции Лапласа, с помощью методов приближенного интегрирования составлены таблицы значений на проме­жутке [0,5] с разной степенью точности. Очевидно, что функция Лапласа является нечетной, следовательно, нет необходимости помещать в таблицу ее значения при отрицательных .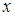

Для случайной величины, распределенной по нормальному закону с параметрами а и 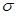, математическое ожидание и дисперсия вычисляются по формулам: 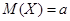, 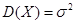.Среднее квадратическое отклонение равно .

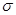Вероятность того, что нормально распределенная величина примет значение из интервала 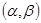, равна

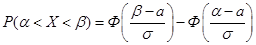, (19.2)

где 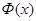есть функция Лапласа, введенная в интегральной предельной теореме.

Часто в задачах требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины X от своего математического ожидания по абсолютной величине не превосходит некоторого значения 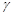, т.е. вычислить вероятность 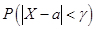. Применяя формулу (19.2), имеем:

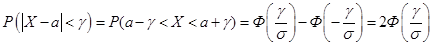. (19.3)

В заключение приведем одно важное следствие из формулы (19.3). Положим в этой формуле 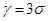. Тогда 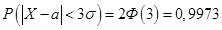, т.е. вероятность того, что абсолютная величина отклонения X от своего математического ожидания не превысит 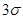, равна 99,73%. Практически такое событие можно считать достоверным. В этом и состоит сущность правила трех сигм.

Правило трех сигм.Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания практически не превосходит утроенного среднего квадратического отклонения.