Регулирование координат в замкнутых структурах
Наличие в электроприводе управляемого преобразователя, питающего якорную цепь или цепь возбуждения, имеющего один или несколько входов и достаточно высокий коэффициент передачи, открывает широкие возможности формирования требуемых искусственных характеристик за счет замыкания системы, т.е. подачи на вход как задающего сигнала, так и сигнала обратной связи по координате, которая должна регулироваться.
Принцип действия замкнутых систем автоматического регулирования координаты рассмотрим на нескольких простейших примерах.
Система УП-Д, замкнутая по скорости
Если жесткость характеристик в разомкнутой системе УП-Д оказывается недостаточной для какого-либо технологического процесса, она может быть повышена посредством замыкания системы по скорости, т.е. использования отрицательной обратной связи по скорости - рис. 3.21,а.
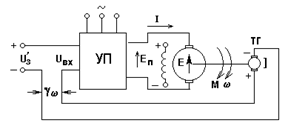
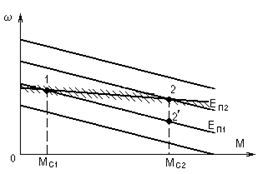
a) б)
Рис. 3.21. Схема (а) и характеристики (б) электропривода постоянного
тока, замкнутого по скорости
К разомкнутой системе (рис. 3.20,а) добавлен измерительный орган - тахогенератор ТГ, сигнал которого ЕТГ = gw сравнивается с задающим сигналом U’з, а разность U’з - gw подается на вход преобразователя (отрицательная обратная связь по скорости). Благодаря этому ЭДС преобразователя теперь определяется не только заданием, но и фактической скоростью вращения. Пусть привод работал в т. 1 (рис. 3.21,б) а затем момент сопротивления увеличился до значения Мс2. В разомкнутой схеме этому изменению соответствовала бы точка 2’, так как изменение Мс не приводило бы к изменению ЭДС преобразователя. В замкнутой системе уменьшение скорости повлечет за собой рост входного сигнала
Uвх = U’з - gw, (3.21)
то есть Еп, следовательно, при Мс2 привод перейдет на характеристику, соответствующую Еп2>Еп1 и будет работать в точке 2. В рассматриваемой схеме 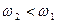 , так как увеличение Uвх, а значит и Еп возможно лишь за счет некоторого уменьшения
, так как увеличение Uвх, а значит и Еп возможно лишь за счет некоторого уменьшения 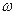 . Такие системы называют статическими, в отличие от астатических, где
. Такие системы называют статическими, в отличие от астатических, где 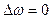 .
.
Получим уравнение механической характеристики в замкнутой системе. Для этого в уравнение (3.20) для разомкнутой системы подставим уравнение замыкания системы (3.21) и получим после простых преобразований:
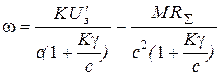 . (3.22)
. (3.22)
Приравнивая выражение для 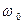 в замкнутой и разомкнутой системах, будем иметь:
в замкнутой и разомкнутой системах, будем иметь:
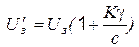 ,
,
то есть для получения одной и той же 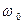 задающее напряжение в замкнутой схеме должно быть взято большим.
задающее напряжение в замкнутой схеме должно быть взято большим.
Сравнив выражение для 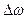 , получим:
, получим:
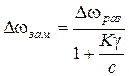 ,
,
то есть перепад скорости при одинаковых нагрузках в замкнутой системе уменьшился в 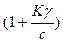 раз.
раз.
Дата добавления: 2015-05-19; просмотров: 698;
