Построение экономико-математической модели оптимизации транспортных процессов
Снижение затратного характера работы ставит перед предприятиями задачу оптимизации транспортных процессов, максимального сокращения расходов, связанных с доставкой продукции производственно-технического назначения от ее изготовителей до потребителей.
При решении задач оптимизации транспортных процессов в качестве критерия оптимальности в основном используется показатель — минимум провозной платы, который успешно применяется для сокращения транспортных расходов поставщиков и потребителей продукции и обеспечивает получение плана перевозок, оптимальных с точки зрения показателей предприятий.
Сложной является проблема определения однородности продукции. Однородность продукции необходимо оценивать не только с точки зрения ее качества, но и по способу транспортировки. Так, некоторые продукты можно перевозить в таре или наливом в цистернах, в специальной упаковке или в контейнерах и т. п. В этих случаях затраты на транспортировку одного и того же продукта будут различными, и по этой причине продукт нельзя считать однородным.
Основной математической моделью, используемой для решения задач оптимального прикрепления потребителей к поставщикам и составления оптимальных планов перевозок, является так называемая транспортная задача линейного программирования (Т-задача).
В общем виде данная задача имеет следующую формулировку:
в m пунктах A1, A2,...,Am производится некоторый однородный продукт, причем объем производства в пункте Ai составляет аi единиц ( i=1, 2, ...,m).
Указанный продукт потребляется в n пунктах В1, В2, ..., Bn, а объем потребления в пункте Вj составляет bi единиц (j=1,2,…,n).
Известны транспортные расходы по перевозке единицы продукции из пункта Ai в пункт Вj, которые равны Cij и приведены в матрице транспортных расходов С:
 |  |
С11 С12 … С1n
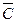= C21 C22 … C2n
Cm1 Cm2 … Cmn
Требуется составить такой план прикрепления потребителей к поставщикам (план перевозок), при котором весь продукт вывозится из пунктов производства и удовлетворяются запросы всех потребителей, а общая величина транспортных издержек является минимальной.
Для составления математической модели данной задачи принимаем количество продукта, перевозимого из пункта Аi в пункт Вj, равным Хij. В этом случае поставленные нами условия можно записать следующим образом.
Определить множество переменных Хij > 0 (i=1, 2, ..., m, j=1. 2, ..., n), удовлетворяющих условиям (1):
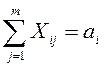; (2.1)
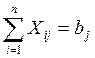, (2.2)
при которых целевая функция
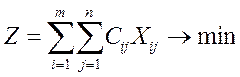(2.3)
достигает минимума.
Условие (2), необходимое и достаточное для разрешимости данной задачи, сводится к балансу
.
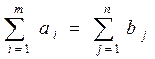Условие (1) характеризует вывоз продукции из всех пунктов производства, а условие (2) означает полное удовлетворение спроса во всех пунктах потребления.
Переменные нумеруют с помощью двух индексов, а набор Хij, удовлетворяющий условиям (1) и (2), записывают в виде матрицы
 |  |
Х11 Х12 … Х1n
= Х21 Х22 … Х2n
Хm1 Хm2 … Хmn
Матрицу Х называют планом перевозок Т-задачи, а переменные Xij - перевозками. План Хопт, при котором целевая функция (2.3) минимальная, называется оптимальным планом.
Рассмотрим пример составления плана перевозок однородного продукта с трех пунктов отправления в четыре пункта назначения при следующих исходных данных:
- ресурсы поставщиков: А1= 170, А2=250 А3=180;
- фонды потребителей: B1=150, B2=230, B3=160, B4=60.
Матрица транспортных расходов дана в табл. 2.1.
Таблица 2.1
Дата добавления: 2015-05-19; просмотров: 739;