Мощности

Производственная мощность представляет собой величину максимально возможного выпуска продукции в единицу времени (за год) при наиболее полном использовании рабочей силы, средств труда, внедрении новой техники и прогрессивных технологий. Производственная мощность отражает способность предприятия по выпуску продукции. На базе этого планирования осуществляется проверка производственной программы и выявление диспропорций, существующих на предприятии между отдельными подразделениями.

Обычно производственную мощность определяют по ведущей группе оборудования. На каждом предприятии существует большое количество групп оборудования, производственные мощности которых различаются. Каждая группа оборудования обладает различной пропускной способностью, режимом работы, трудоемкостью выполняемых операций.

Производственную мощность предприятия нельзя определять по наибольшей пропускной способности какой-либо группы оборудования. Ведущая группа оборудования определяется по специальной инструкции.

1. x_{ij 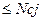;} (j = 1,n); (1.20)

2. 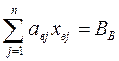; (1.21)

3. 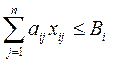(i=1,m); (1.22)

Z = 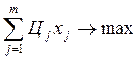, (1.23)

где x_j – искомая величина выпуска j-й продукции в натуральном выражении;

N_cj – объем спроса на j-ю продукцию в натуральном выражении;

a_вj – норма затрат станочного времени по ведущей группе оборудования

на производство j-й продукции;

B_B – ресурс рабочего времени ведущей группы оборудования;

a_ij – норма затрат станочного времени по i-й группе оборудования на

производство j-й продукции;

B_i – ресурс рабочего времени i-й группы оборудования;

m – количество различных групп оборудования;

n– количество номенклатурно-ассортиментных позиций;

Ц_j – оптовая цена за единицу j-й продукции.

Смысл ограничений:

1) первое – отображает условие того, что выпуск j-й продукции не должен превышать объем спроса на эту продукцию;

2) второе показывает, что пропускная мощность предприятия должна соответствовать пропускной мощности ведущей группы оборудования;

3) третье – выявляет существующие на предприятии диспропорции между группами оборудования, то есть по каждой группе оборудования выявляется его пропускная способность и определяется больше или меньше она производственной мощности предприятия.

Целевая функция отображает условие выпуска максимума продукции в стоимостном выражении.

5. Экономико-математическая модель оптимизации раскроя материала

Значительная часть различных материальных ресурсов поступает на предприятие в виде стандартных материалов определенного профиля, габарита и размеров. В последующем весь этот материал для получения необходимых заготовок приходится раскраивать. На предприятиях различных отраслей используются различного вида стандартные материалы: лист фанеры, стальной прут, трубы и т.д.

Раскрой используемого материала необходимо делать с таким расчетом, чтобы полностью обеспечить производственную программу необходимыми заготовками и израсходовать на нее как можно меньше материала, т.е. минимизировать расходы.

1. 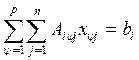(i=1,m); (1.29)

2. 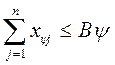( 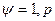); (1.30)

Z = 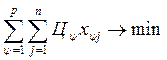, (1.31)

где p – количество различных видов стандартного материала, используемого

при раскрое;

n – количество различных вариантов раскроя из единицы 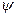- го вида

стандартного материала;

A_{i 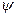j} – количество i-х заготовок, получаемых из единицы материала 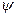- го

вида, при раскрое по j‑му варианту;

x 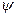_j – количество стандартных единиц материала 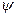- го вида, раскраиваемых по j‑му варианту;

b_i – потребность в i-х заготовках;

B 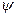- максимальное количество 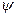- го вида стандартного материала, которое

может быть использовано при раскрое;

Ц 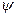- цена единицы стандартного материала 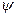- го вида.

Смысл ограничений:

1) первое – отображает условие изготовление i-й заготовки в требуемом от производства количестве;

2) второе показывает, что суммарный расход материалов не должен превышать выделенных ресурсов.

Целевая функция означает, что суммарные затраты на производство должны быть минимальны.

В том случае, когда предприятие получает один вид материала для выполнения производственной программы (р = 1), применяется упрощенная математическая модель.

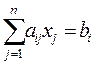(i = 1,m); (1.32)

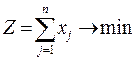, (1.33)

где а_ij – количество i-х заготовок, полученных при j-м варианте раскроя;

х_j – количество материала стандартного вида, используемого по j-му

варианту раскроя.

Информационное обеспечение модели.

В данной ЭММ все информационные элементы изначально задаются конкретными условиями. Необходимо знать производственную программу, потребность в заготовках, лимиты. В модели остается неясной информация о возможных вариантах раскроя (а), которую необходимо определить. Решение этой задачи зависит от того, какой исходный материал получает предприятие и какие заготовки необходимо из него выкроить. Задача является трудноразрешимой, если раскрой осуществляется в 2 измерениях. В связи с тем, что количество возможных вариантов раскроя велико и перебрать их практически невозможно, как правило, ищут варианта раскроя материала по первой заготовке, а из получаемых отходов получают заготовки меньшего размера. Опытным путем составляется 10-15 вариантов раскроя и на их основе строится модель.

Если раскрой материала осуществляется в одном измерении, то возможно перебрать все варианты.

При поиске вариантов раскроя строится специальная таблица. В первом столбце такой таблицы располагаются номера вариантов раскроя, в последнем –остаток материала, а в промежутке между ними – столбцы, содержащие размеры заготовок. Причем в столбцах размеры заготовок должны располагаться в порядке убывания.

Перебору подлежат только рациональные варианты раскроя. Рациональными считаются такие варианты, при которых в остатке будет материал размером меньше самой маленькой из выкраиваемых заготовок.

В первом варианте раскроя принимается максимальное количество наибольших по размеру заготовок. Остаток материала перераспределяется между остальными заготовками. При переборе вариантов из полученного остатка пытаются выкроить максимальное количество заготовок, расположенных в третьем столбце таблицы. В последующих вариантах количество этих заготовок сокращается на одну до тех пор, пока их количество не станет равным нулю. Как только получен нуль в третьем столбце, в последующих вариантах пытаются получить максимальное количество заготовок расположенных в четвертом столбце, а затем их количество также постепенно сокращают до нуля. Эта процедура выполняется до тех пор, пока в предпоследнем столбце таблицы не будет получено максимальное количество заготовок наименьшего размера, а в остальных столбцах, за исключением второго, будут находиться нули. После этого количество заготовок наибольшего размера (расположенных во втором столбце) сокращается на единицу и вся процедура повторяется. В самом последнем варианте раскроя в предпоследнем столбце таблицы будет находиться максимальное количество заготовок наименьшего размера, а во всех промежуточных столбцах, содержащих размеру заготовок, будут находиться нули.

Проиллюстрируем эту процедуру примером.

Пусть у нас имеется некоторое количество единиц стандартного материала размером 1000 мм. Из этого стандартного материала нам необходимо выкроить некоторое количество заготовок трех размеров: 350, 220 и 150 мм. Найдем возможные варианты раскроя стандартного материала (табл. 1.3).

Таблица 1.3

Схема построения вариантов раскроя

Итак, в результате найдено десять вариантов раскроя единицы стандартного материала, которые и будут использованы в дальнейшем в математической модели данной задачи.

ТРАНСПОРТНАЯ ЗАДАЧА