Оптимизационные модели линейного программирования

1. Экономико-математическая модель оптимизации производственной программы

Производственная программа – это планируемый объем произведенной продукции в натуральном и стоимостном выражении за определенный период времени. План производства продукции разрабатывается в рамках бизнес-плана предприятия. В данном разделе необходимо рассмотреть:

1) где будет производиться продукция (работы, услуги);

2) необходимо ли создать новые производственные мощности или возможно переоснастить действующее производство;

3) каков оптимальный объем производства на предприятии;

4) какие необходимы инвестиции для достижения оптимальной мощности;

5) как будет обеспечено предприятием сырье, комплектующими изделиями;

6) какие будут использоваться технологии и оборудование;

7) будет ли предприятие работать в кооперации с другими предприятиями.

Математическая модель позволяет установить производственную программу предприятия, оптимизировав ее величину с учетом имеющихся ресурсов и выбранной целевой функции.

1. х_{j 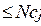;} (j = 1,n); (1.10)

2. 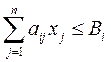(i=1,m) ; (1.11)

Z = 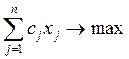, (1.12)

где x_j – искомая величина выпуска j-й продукции в натуральном выражении;

N_cj – объем спроса на j-ю продукцию в натуральном выражении;

a_ij – норма расхода i-го ресурса на единицу j-й продукции;

B_i – объем выделенного i – го ресурса;

с_j – прибыль предприятия от реализации продукции;

m – номенклатура используемых ресурсов;

n – номенклатура выпускаемой продукции.

Смысл ограничений:

1) первое ограничение устанавливает величину производства j-й продукции в размере, не превышающем объем существующего на рынке спроса;

2) второе ограничение устанавливает возможность выпуска j-й продукции в соответствии с имеющимся лимитом i-го ресурса.

Целевая функция устанавливает требование максимизации прибыли от выпуска всех видов продукции.

2. Экономико-математическая модель оптимизации использования

оборудования на предприятии

Постановка задачи: на заводе железобетонных изделий установлено взаимозаменяемое оборудование (количество моделей оборудования – m). На этом оборудовании можно выполнять операции по изготовлению арматуры n-го количества типоразмера. Необходимо составить оптимальную структуру загрузки оборудования таким образом, чтобы максимизировать объем изготовления арматуры, потребность в которой неограниченна.

1. 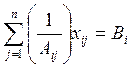(i=1,m); (1.13)

2. 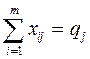(j=1,n); (1.14)

3. 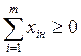; (1.15)

Z= 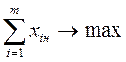, (1.16)

где x_ij – искомая величина производства j-го типоразмера арматуры на станках

i-го оборудования;

А_ij – часовая производительность i-го оборудования при производстве j-го

типоразмера арматуры;

В_i – фонд рабочего времени i-й группы оборудования;

q_j – суточная потребность в арматуре j-го типоразмера, кроме позиции

потребность в которой не ограничена;

х_ij – искомая величина, потребность в которой не ограничена;

m – количество различных взаимозаменяемых моделей оборудования;

n – количество различных типоразмеров арматуры.

Смысл ограничений:

1) первое – отображает возможность выпуска j-го типоразмера арматуры в пределах фонда времени работы оборудования i-й модели;

2) второе – показывает, что искомая величина производства j-го типоразмера арматуры на станке i-й модели оборудования должна быть равна суточной потребности в арматуре j – го типоразмера, кроме позиции, потребность в которой не ограничена;

3) третье отображает условие того, что искомая величина производства j-го типоразмера арматуры, потребность в которой не ограничена, должна быть больше.

Целевая функция максимизирует объем выпуска арматуры j-го типоразмера, потребность в которой не ограничена