П.4. Модели взаимодействия двух популяций
Любые популяции существуют во взаимодействии с окружением. Взаимодействовать могут как биологические виды в собственном смысле этого слова, так и разновидности одного вида, например, различные мутанты одного и того же вида микроорганизмов при их культивировании. Взаимодействия принято разделять на трофические (когда один из видов питается другим видом) и топичес-кие (взаимодействия между видами одного трофического уровня). Более подробно типы взаимодействий рассмотрены в статье «Экология математическая»*. В популяционной динамике принято классифицировать взаимодействия по их результатам. Наиболее распространенными и хорошо изученными являются взаимодействия конкуренции (когда численность каждого из видов в присутствии другого растет с меньшей скоростью), симбиоза (когда виды способствуют росту друг друга) и типа хищник-жертва или паразит-хозяин (когда численность вида-жертвы в присутствии вида-хищника растет медленнее, а вида-хищника - быстрее). В природе также встречаются взаимодействия, когда один из видов чувствует присутствие второго, а другой - нет (аменсализм и комменсализм), или виды нейтральны.
Первое глубокое математическое исследование закономерностей динамики взаимодействующих популяций дано в монографии Вито Вольтерра* «Математическая теория борьбы за существование». В своей монографии ученый предложил описывать взаимодействие видов подобно тому, как это делается в статистической физике и химической кинетике, в виде мультипликативных членов в уравнениях (произведений численностей взаимодействующих видов). Тогда в общем виде с учетом самоограничения численности по логистическому закону система дифференциальных уравнений, описывающая взаимодействие двух видов, может быть записана в форме:
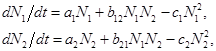 (П.3.3)
(П.3.3)
где параметры ai - константы собственной скорости роста видов, ci - константы самоограничения численности (внутривидовой конкуренции), bij - константы взаимодействия видов, (i,j=1,2). Соответствие знаков этих последних коэффициентов различным типам взаимодействий приведено в табл. П.3.1.
| Таблица П.3.1 | |||
| ТИПЫ ВЗАИМОДЕЙСТВИЯ ВИДОВ | |||
| СИМБИОЗ | + | + | b12, b21> 0 |
| КОММЕНСАЛИЗМ | + | b12 > 0, b21= 0 | |
| ХИЩНИК-ЖЕРТВА | + | - | b12 > 0, b21< 0 |
| АМЕНСАЛИЗМ | - | b12 = 0, b21< 0 | |
| КОНКУРЕНЦИЯ | - | - | b12, b21 < 0 |
| НЕЙТРАЛИЗМ | b12, b21 = 0 |
Исследование свойств моделей типа (П.3.3) приводит к некоторым важным выводам относительно исхода взаимодействия видов.
Уравнения конкуренции (b12 > 0, b21 < 0) предсказывают выживание одного из двух видов, в случае если собственная скорость роста другого вида меньше некоторой критической величины. Оба вида могут сосуществовать, если произведение коэффициентов межпопуляционного взаимодействия меньше произведения коэффициентов внутри популяционного взаимодействия: b12b21 < c1c2..
Для изучения конкуренции видов ставились эксперименты на самых различных организмах. Обычно выбирают два близкородственных вида и выращивают их вместе и по отдельности в строго контролируемых условиях. Через определенные промежутки времени проводят полный или выборочный учет численности популяции. Регистрируют данные по нескольким повторным экспериментам и анализируют. Исследования проводили на простейших (в частности, инфузориях), многих видах жуков рода Tribolium, дрозофиллах, пресноводных ракообразных (дафниях). Много экспериментов проводилось на микробных популяциях. В природе также проводили эксперименты, в том числе на планариях (Рейнольдс) двух видах муравьев (Понтин). Результаты свидетельствуют о существовании конкуренции, ведущей к уменьшению численности обоих видов.
Модель конкуренции типа (П.3.3) имеет недостатки, в частности, из нее следует, что сосуществование двух видов возможно лишь в случае, если их численность ограничивается разными факторами, но модель не дает указаний, насколько велики должны быть различия для обеспечения длительного сосуществования. Внесение стохастических элементов (например, введение функции использования ресурса) позволяет ответить на эти вопросы.
Для взаимоотношений типа хищник-жертва или паразит-хозяин система уравнений (П.3.3) принимает вид:
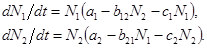 (П.3.4)
(П.3.4)
При различных соотношениях параметров в системе возможно выживание только жертвы или только хищника (если у него имеются и другие источники питания), а также возможно сосуществование обоих видов. В этом случае численности видов совершают колебания, причем колебания численности хищника в модели запаздывают по отношению к колебаниям численности жертвы (рис. П.3.3).
 На вопрос о том, отражает ли модель (П.3.4) природные закономерности ответить не так просто. В реальности колебания численностей хищника и жертвы наблюдались как в природных, так и в экспериментальных ситуациях (рис. 2.6, Гл.2).
На вопрос о том, отражает ли модель (П.3.4) природные закономерности ответить не так просто. В реальности колебания численностей хищника и жертвы наблюдались как в природных, так и в экспериментальных ситуациях (рис. 2.6, Гл.2).
 Однако, существует много важных аспектов экологии хищника и жертвы, которые в модели не учтены. Даже если в популяции наблюдаются регулярные колебания численности, это вовсе не обязательно служит подтверждением модели Вольтерра, логистической модели с запаздыванием (2.8, Гл.2) или любой другой простой модели. Колебательное изменение численности популяции в природе может отражать ее взаимодействие с пищевыми объектами или с хищниками. Численность хищников может повторять эти циклы даже в том случае, если само взаимодействие их не вызывает. При описании любой конкретной ситуации требуется построение гораздо более подробной модели, чаще всего имитационной (см. Биология математическая), и необходима большая работа по идентификации параметров такой модели, лишь тогда можно надеяться на правдоподобное моделирование природной ситуации.
Однако, существует много важных аспектов экологии хищника и жертвы, которые в модели не учтены. Даже если в популяции наблюдаются регулярные колебания численности, это вовсе не обязательно служит подтверждением модели Вольтерра, логистической модели с запаздыванием (2.8, Гл.2) или любой другой простой модели. Колебательное изменение численности популяции в природе может отражать ее взаимодействие с пищевыми объектами или с хищниками. Численность хищников может повторять эти циклы даже в том случае, если само взаимодействие их не вызывает. При описании любой конкретной ситуации требуется построение гораздо более подробной модели, чаще всего имитационной (см. Биология математическая), и необходима большая работа по идентификации параметров такой модели, лишь тогда можно надеяться на правдоподобное моделирование природной ситуации.
Дата добавления: 2015-05-19; просмотров: 1140;
