П.5. Обобщенные модели взаимодействия популяций двух видов

С середины XX века в связи с развитием интереса к экологии и с быстрым усовершенствованием компьютеров, позволившим численно решать и исследовать системы нелинейных уравнений, стало развиваться направление популяционной динамики, посвященное выработке общих критериев с целью установить, какого вида модели могут описать те или иные особенности поведения численности взаимодействующих популяций, в частности, устойчивые колебания.

Эти работы развивались по двум направлениям. Представители первого направления, описывая входящие в модельные системы функции, задают лишь качественные особенности этих функций, такие как положительность, монотонность отношения типа больше, меньше (Колмогоров, 1972, Rosenzweig, 1969). Рассматриваемые здесь модели могут быть изучены аналитически.

В рамках второго направления последовательно рассматривались различные модификации системы Вольтерра, получаемые включением в исходную систему различных дополнительных факторов и закономерностей, описываемых явными функциями (Холлинз, 1965, Иевлев,1955, Полуэктов, 1980, Базыкин, 1985, Медвинский, 1995). Использование компьютерной техники позволило применить полученные здесь результаты к конкретным популяциям, в частности, к задачам оптимального промысла.

Примером работ первого направления служит работа А.Н.Колмогорова (1935, переработана в 1972), который рассмотрел обобщенную модель взаимодействия биологических видов типа хищник-жертва или паразит-хозяин. Модель представляет собой систему двух уравнений общего вида

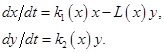(П.3.5)

В модель заложены следующие предположения: 1) Хищники не взаимодействуют друг с другом, т.е. коэффициент размножения хищников k₂ и число жертв L, истребляемых в единицу времени одним хищником, не зависит от y. 2) Прирост числа жертв при наличии хищников равен приросту в отсутствие хищников минус число жертв, истребляемых хищниками. Функции k₁(x), k₂(x), L(x), - непрерывны и определены на положительной полуоси x,y, 0. 3) dk₁/dx < 0. Это означает, что коэффициент размножения жертв в отсутствие хищника монотонно убывает с возрастанием численности жертв, что отражает ограниченость пищевых и иных ресурсов. 4) dk₂/dx > 0, k₂(0) < 0 < k₁(¥). С ростом численности жертв коэффициент размножения хищников монотонно возрастает, переходя от отрицательных значений, (когда нечем питаться) к положительным. 5) Число жертв, истребляемых од-

ним хищником в единицу времени L(x) > 0 при N > 0; L(0) = 0.

Исследование этой модели и ее частных случаев, например, модели Розенцвейга (1965,1969), привело к выводу о том, что регулярные колебания в системе имеют место, если численность хищника ограничивается численным количеством особей жертвы. Если численность жертвы ограничивается количеством необходимых ей ресурсов, или численность хищника ограничивается не количеством жертвы, а другим фактором, это приводит к затухающим колебаниям. К затуханию колебаний приводит также наличие убежищ для жертв, которые делают их недоступными для хищников. Амплитуда колебаний будет возрастать, и это приведет в конце концов к вымиранию одного или обоих видов, если хищник может прокормиться при такой плотности популяции жертв, которая значительно ниже допустимой емкости среды, которая следует из логистического уравнения.

Особый интерес для практики представляет выработка критериев близости системы к опасным границам, при переходе через которые система перестает существовать или переходит в качественно иное состояние. При этом характер динамики популяции резко меняется, например, популяция переходит от монотонного роста к резким колебаниям численности, или просто вымирает. Такие границы называются бифуркационными. Исследование свойств моделей показывает, что одним из признаков близости к опасной границе является очень медленное восстановление численности после воздействия неблагоприятного фактора. Индикатором опасности служит также изменение формы колебаний численностей хищника и жертвы. Если из близких к гармоническим колебания становятся релаксационными, то есть характерные времена изменения численности видов начинают сильно различаться, причем амплитуда колебаний со временем нарастает, это может привести к потере устойчивости системы и вымиранию одного или обоих видов.

Мы рассмотрели простейшие модели популяционной динамики: модели одного или двух взаимодействующих видов. Такие модели допускают аналитическое исследование, и потому достаточно полно изучены. Дальнейшее углубление математической теории идет по линии детализации структуры самих популяций (возрастной, половой) и учета временных и пространственных факторов.

Учет запаздывания в моделях взаимодействующих видов приводит к системам уравнений, изучение существования и устойчивости которых представляет серьезную математическую проблему, а сами решения, описывающие динамику численности, могут носить не только колебательный, но и квазистохастический характер, как это мы видели для дискретных моделей популяций с неперекрывающимися поколениями. Устойчивость или неустойчивость модели может зависеть от периода запаздывания, и зависимость эта может быть немонотонной и даже многоэкстремальной. В последние годы для систем с запаздыванием используется понятие абсолютной устойчивости, справедливое для систем, которые локально устойчивы независимо от величины запаздывания.

Обычно не все члены уравнений содержат запаздывание. Например, увеличение численности популяции может сказаться на скорости роста лишь через определенное время, когда молодые особи достигнут репродуктивного возраста, а хищничество сокращает численность жертв в тот же момент времени и не содержит запаздывания. Исследование учитывающих эти обстоятельства моделей показывает, что саморегулирование жертв стабилизирует систему, а запаздывание в реакции хищника - дестабилизирует. Короткие времена запаздывания в размножении как хищника, так и жертвы могут как стабилизировать, так и дестабилизировать систему. Последний вывод опровергает общепринятое ранее представление о том, что малое запаздывание слабо сказывается на поведении системы. Интуитивное представление о том, что чем больше запаздывание, тем больше его дестабилизирующий эффект, неправильно. В некоторых системах взаимодействующих видов оказалось, что малые времена запаздывания наиболее опасны для стабильности системы.

Моделирование конкретных сообществ часто требует подробной детализации половой и возрастной структуры. Взаимодействие возрастных групп даже в пределах одного вида приводит к сложным типам динамики численности. Рассмотрим в качестве примера модель, описывающую динамику численности насекомых с полным метаморфозом с двумя активными стадиями имаго и личинок. Уравнения имеют вид:

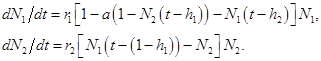(П.3.6)

Здесь N₁ = N₁(t), N₂ = N₂(t) - нормированные количества имаго и личинок, h₁ - время между по-

явлением личинок и имаго, (1- h₁) - время между появлением имаго и личинок, r₂ - скорость появле-

ния личинок, 0 < a < 1, r(1-a) = r₁ - мальтузианский коэффициент линейного роста, который определяется по плодовитости имаго, h₂ – среднее время жизни в течение одного года популяции имаго.

К сказанному о межвидовой борьбе в биоценозе, следует доба­вить, что в 90-х годах XX в. английские и канадские ученые пришли к выводу, что в лесах деревья и кустарники, наоборот, помогают друг другу благодаря действию законов всеобщей поддержки. Информа­ция, которая обеспечивает такое взаимодействие, передается под Землей благодаря грибку микориза, имеющихся на корнях всех растений.

Из приведенной характеристики биоценозов ясно, что их устойчивость (гомеостаз) зависит прежде всего от изменений в структуре сообществ, от уменьшения видового разнообразия, от изменений трофической цепи и, в известной мере, от дезорганизации регуляции биоценоза с помощью аллелохимических факторов и др.

В заключение следует отметить, что математические модели - не только средство для количественного описания явлений. Модель сложной системы - это математический образ, позволяющий формализовать и обобщить в терминах теории представления о многочисленных свойствах и характеристиках сложной системы. Расширение понятийного и образного круга не меньше чем количественные расчеты представляет собой ценный результат междисциплинарных исследований с применением аппарата математики и физики для изучения живых систем. В этом смысле популяционная динамика занимает особое место. При всей ограниченности «числа особей», как характеристики вида или сообщества, значение термина «численность» имеет четкий и универсальный смысл.

Популяционная динамика представляет собой область математической биологии, описывающая с помощью моделей типы динамического поведения развивающихся систем, представляющих собой одну или несколько взаимодействующих популяций или внутрипопуляционных групп. Отличительной чертой биологических популяций, как и всех живых систем, является их удаленность от термодинамического равновесия, использование для своего роста и развития энергии внешних источников. Это обуславливает необходимость использования для описания таких систем нелинейных моделей, позволяющих отразить основные характерные черты популяционной динамики лабораторных и природных популяций. Это - ограниченность роста, вызванная совокупностью факторов. Возможность нескольких стационарных исходов в зависимости от начальных условий роста популяции. «Зависание» системы вблизи критической границы и ее чувствительность в этой области к малым флуктуациям и индивидуальным усилиям. Запаздывание реакции системы на изменение внешних факторов. Возможность колебательных и квазистохастических режимов. Математические результаты, полученные при изучении моделей популяционной динамики, служат для практических целей управления биотехнологическими и природными системами и, дают пищу для развития собственно математических теорий.