П.1. Динамика численности популяций

Постановка математических задач в терминах популяционной динамики восходит к глубокой древности. Человеку свойственно рассуждать о предметах, жизненно ему близких, и что может быть ближе, чем законы размножения популяций – людей, животных, растений.

Первая дошедшая до нас математическая модель динамики популяций приводится в книге «Трактат о счете» "Liber abaci", датированной 1202 годом, написанной крупнейшим итальянским ученым Леонардо Фибоначчи - Леонардо из Пизы, (предположительно 1170-1240). В этой книге, представляющей собой собрание арифметических и алгебраических сведений того времени и впоследствии распространившейся в списках по всей Европе, рассматривается следующая задача. «Некто выращивает кроликов в пространстве, со всех сторон обнесенном высокой стеной. Сколько пар кроликов рождается в один год от одной пары, если через месяц пара кроликов производит на свет другую пару, а рожают кролики, начиная со второго месяца после своего рождения». Решением задачи является ряд чисел:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ... (*)

(Сам Леонардо опустил первый член ряда). Два первых числа соответствуют первому и второму месяцу размножения. 12 последующих – месячному приросту поголовья кроликов. Каждый последующий ряд равен сумме двух предыдущих. Ряд (*) вошел в историю как ряд Фибоначчи, а его члены - чисел Фибоначчи. Это первая известная в Европе рекурсивная последовательность чисел (в которой соотношение между двумя или более членами ряда может быть выражена в виде формулы). Рекуррентная формула для членов ряда Фибоначчи была записана французским математиком Альбертом Гирером в 1634 г.

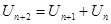
Здесь U представляет собой член последовательности, а нижний индекс ‑ его номер в ряду чисел. В 1753 г. математик из Глазго Роберт Симпсон заметил, что при увеличении порядкового номера членов ряда отношение последующего члена к предыдущему приближается к числу a, называемому «Золотым сечением», равному 1,6180..., или 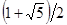. В 19 веке о свойствах ряда Фибоначчи и его связи с Золотым сечением много писал французский математик Эдуард Лукас. С тех пор естествоиспытатели наблюдают его закономерности в расположения чешуек на шишках, лепестков в цветке подсолнуха, в спиральных образованиях ракушек моллюсков и других творениях природы. Ряд Фибоначчи и его свойства также используются в вычислительной математике при создании специальных алгоритмов счета.

Модель экспоненциального роста численности населения предложена Мальтусом в 1798 г. в его классическом труде «О росте народонаселения». Томас Роберт Мальтус (1766-1834) известный английский демограф и экономист, обратил внимание на тот факт, что численность популяции растет по экспоненте (в геометрической прогрессии), в то время как производство продуктов питания растет со временем линейно (в арифметической прогрессии), из чего сделал справедливый вывод, что рано или поздно экспонента обязательно «обгонит» линейную функцию, и наступит голод. На основании этих выводов Мальтус говорит о необходимости ввести ограничения на рождаемость, в особенности для беднейших слоев общества. «Экономический пессимизм», следующий из прогнозов предложенной им модели, в основу которой положен анализ эмпирических данных, Мальтус противопоставлял модным в начале 19 века оптимистическим идеям гуманистов: Жана Жака Руссо, Уильяма Годвина и других, предсказывающих человечеству грядущее счастье и процветание. Можно говорить о том, что Мальтус был первым ученым «алармистом», который на основании результатов моделирования «бил тревогу» и предупреждал человечество об опасности следования развитию по используемым ранее сценариям прогресса. Во второй половине 20 века такую «алармистскую» роль сыграли работы Римского клуба, и в первую очередь «модель глобального роста» Дж. Форрестера.

В настоящее время уже достаточно моделей, подтверждающих логистическую модель, как на чисто природных объектах, так и на природно-антропогенных. Например, А.М. Гиляров приводит сведения о размножении северных оленей, интродуцированных (вселенных в местообитания, где они раньше не проживали) на острова Берингова моря. С небольших когорт, состоящих из нескольких десятков особей, в течение ряда лет рост численности по экспоненциальному закону приводил к возникновению популяции оленей, состоящей из нескольких тысяч голов. Затем наблюдалось резкое падение численности тоже до нескольких десятков голов за короткое время, один – три года. Причина – полный расход пищевых ресурсов, которыми обладали эти острова.

Г.Ф. Гаузе экспериментально исследовал конкуренцию двух видов инфузорий: Paramecium candatum и Paramecium aurelia. Их культивировали раздельно и вместе, используя строго дозированную бактериальную пищу. При раздельном культивировании их численность росла по обычной S-образной кривой, при совместном ‑ побеждали в конreрентной борьбе P. aurelia (см. рис. 2.8). Поражение P. candatum объясняется тем, что она плохо переносила накопление в среде продуктов метаболизма бактерий и размножалась медленнее. Но при смене пищи, например, при замене ее на дрожжи, побеждала ужe P. candatum, так как в благоприятных для обоих видов условиях она имела преимущество за счет способности к более быстрому размножению и увеличению своей численности.