Теоретическое описание эффекта поля
Проверку проводят с помощью моментоскопа КИ-4941 и угломера КИ-13926. Моментоскоп устанавливают на проверяемую секцию топливного насоса и, медленно прокручивая коленчатый вал, заполняют стеклянную трубку моментоскопа топливом. Наблюдая за уровнем топлива в трубке моментоскопа, прокручивают коленчатый вал до момента начала подъема уровня топлива в трубке. Затем на шкив коленчатого вала устанавливают угломер и медленно прокручивают коленчатый вал по направлению вращения до прихода поршня первого цилиндра в в.м.т. По перемещению пузырька воздуха в угломере .определяют угол начала нагнетания топлива. Способы фиксации в.м.т. поршня или положения коленчатого вала, соответствующего установочному углу опережения нагнетания топлива, указаны в таблице 11.3.
При проверке и регулировке насосов с изношенными плунжерными парами, угол опережения подачи проверяют при установке технологической пружины (из комплекта КИ-4У4П под штуцер головки топливного насоса.
Если величина угла выходит за пределы допустимого, то повернуть шлицевую шайбу относительно шестерни привода топливного насоса (для увеличения угла шайбу поворачивают по часовой стрелке).
Таблица 11.3 Номинальные значения угла опережения подачи топлива
| Марка двигателя | Способ определения «ВМТ» поршня или положения коленчатого вала, соответствующего установочному углу начала подачи топлива | Угол опережения подачи топлива, град. до «ВМТ» |
| СМД – 14/15/19/20 /21/22 | Установочная шпилька входит в углубление на маховике | 20…22 |
| СМД – 17/18 | То же | 27…29 |
| СМД – 31 | «…» | 27…30 |
| А – 01М, Д – 440/442 | «…» | 27…32 |
| А – 41 | «…» | 29…34 |
| Д – 21А | Метка «Т» на шкиве привода вентилятора совпадает со стрелкой указателя «ВМТ», закрепленного на крышке распред. шестерен | 24…26 |
| Д – 144 – 07/0929/60 | То же | 24…32 (с насосом УТН) 26…28 (с насосом НД21/4) |
| Д – 144 – 24/28/30/66/67 /70/71/72/81 | «…» | 30…32 (с насосом УТН) 24…26 (с насосом НД21/4) |
| Д – 144 – 25/26/73/80 /80 - 1 | «…» | 30…32 (с насосом УТН) 22…24 (с насосом НД21/4) |
| Д - 120 | «…» | 26…28 (для модификаций двигателя с эксплуатационной мощностью 22,1кВт), 24…26 (для модификаций двигателя с эксплуатационной мощностью 18,4кВт) |
| СМД – 62 | Указатель «ВМТ» совпадает с углублением на маховике | 26…28 |
| Д – 240/241/243/245 | Установочная шпилька входит в углубление на маховике | 23…25 |
| Д – 242/244, Д – 65 | То же | 21…23 |
| ЯМЗ – 238 | Цифра на маховике совпадает с соответствующей цифрой на торце муфты опережения подачи топлива | 17…19 |
| ЯМЗ - 240 | Риска на корпусе гасителя крутильных колебаний совпадает со стрелкой указателя на маховике | 18…20 |
| КАМАЗ | Фиксатор, расположенный на картере маховика, входит в паз маховика | 42…43 |
| ЗИЛ - 645 | Метка на торце муфты опережения подачи топлива совпадает с меткой на корпусе насоса | 18…20 |
Теоретическое описание эффекта поля
Эффектом поля называют явление изменения приповерхностной проводимости под действием перпендикулярно приложенного электростатического поля. Различают стационарный и нестационарный эффекты поля. В стационарном эффекте поля изменение проводимости совпадает с изменением поля (носители или заряд ОПЗ успевают следовать за полем). В нестационарном эффекте поля заряд неосновных носителей не успевает за изменением поля и не вносит дополнительную емкость, соответствующую стационарному случаю. Любое изменение проводимости полупроводникового образца, связанное с поверхностным слоем, является функцией изгиба энергетических зон на поверхности. Поэтому удобно ввести понятие избыточной поверхностной концентрации, определяемой как добавочное число свободных носителей на единицу площади поверхности, вызванное изгибом зон.
Значения ∆N и ∆P могут быть вычислены в функции поверхностного электростатического потенциала Ys следующим образом:
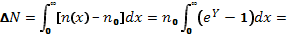
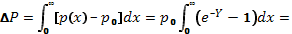

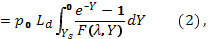
где 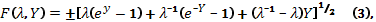
где «+» для Y > 0, «-» для Y < 0,
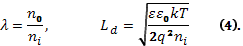
Избыточные электроны и дырки могут двигаться вдоль поверхности при приложении электрического поля, обусловливая тем самым изменение проводимости образца. Вызванная наличием ∆N и ∆Р избыточная проводимость носит название поверхностной проводимости. Если предположить, что значение подвижностей электронов и дырок в области пространственного заряда равно их значениям в объеме полупроводника, то для поверхностной проводимости в единицах [Ом-1] можно написать:
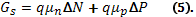
Поскольку ∆N и ∆Р являются функциями уровня легирования и поверхностного электростатического потенциала Ys, то и Gs является функцией тех же величин.
На рисунке 1 приведены графики зависимости Gs(Ys) для различных значений λ в полупроводнике n-типа.
При Ys = 0 — случай «плоских зон», поверхностная проводимость Gs = 0.
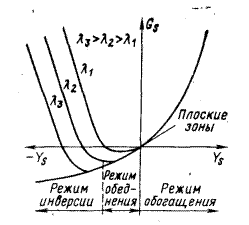 Для положительных значений Ys концентрация основных носителей заряда в области пространственного заряда растет, поверхностная проводимость Gs > 0 и монотонно возрастает с ростом Ys (правая часть на рисунке 1). Это соответствует режиму обогащения.
Для положительных значений Ys концентрация основных носителей заряда в области пространственного заряда растет, поверхностная проводимость Gs > 0 и монотонно возрастает с ростом Ys (правая часть на рисунке 1). Это соответствует режиму обогащения.
Рисунок 1 – График зависимости поверхностной проводимости Gs от поверхностного электростатического потенциала Ys для различных уровней легирования.
При отрицательном Ys поверхностная проводимость Gs отрицательна и с ростом |Ys| уменьшается, поскольку концентрация подвижных носителей заряда в области пространственного заряда меньше, чем в случае Ys = 0. Это соответствует режиму обеднения. Эта ситуация будет иметь место до тех пор, пока скорость нарастания неосновных носителей заряда — в данном случае дырок — с изменением Ys не станет больше, нежели скорость убывания концентрации основных носителей заряда — электронов. Это соответствует условию n0 = ps, т. е. концентрация электронов в объеме полупроводника равна концентрации дырок на поверхности.
Последующее увеличение |Ys| приводит к резкому увеличению концентрации дырок, образованию инверсионного слоя и, следовательно, к увеличению поверхностной проводимости Gs. Все эти участки кривой Gs (Ys) приведены на рисунке 1. До этого мы полагали, что значения подвижностей носителей заряда в объеме и в слое пространственного заряда вблизи поверхности равны. Однако это не так в том случае, когда при соударении с поверхностью носитель заряда полностью или частично теряет дрейфовую составляющую скорости. Это так называемое диффузное рассеяние, в той или иной степени имеющее место в подавляющем числе практических случаев. Диффузное рассеяние приводит к уменьшению подвижности носителя заряда, движущегося в потенциальной яме (основного носителя заряда в случае слоев обогащения и неосновного — в случае слоев инверсии). Физической причиной снижения подвижности является то, что появление поля, нормального к поверхности, приводит к увеличению составляющей скорости к поверхности и, как результат этого, уменьшается время соударения носителя заряда с поверхностью.
Изменение подвижности в приповерхностной области учитывается поправкой Шриффера по формуле:
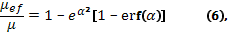
где
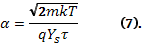
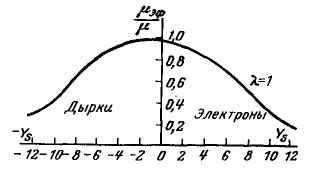
Рисунок 2 – График зависимости подвижности носителей заряда в слое пространственного заряда от поверхностного электростатического потенциала в случае полного диффузного рассеяния.
Наиболее эффективным способом управления значением поверхностного электростатического потенциала (а следовательно, и значением поверхностной проводимости Gs и емкости пространственного заряда полупроводника Csp) является приложение к полупроводнику электрического поля, нормального к поверхности полупроводника. Это сравнительно просто достигается в структуре, где полупроводник служит одной из обкладок конденсатора, отделенной от второй обкладки — металлического электрода — слоем диэлектрика (так называемая МДП-структура).
Экспериментально снимается зависимость изменения проводимости образца при вариации значения потенциала Vq, приложенного к металлическому электроду. Из диаграммы, представленной на рисунке 4, следует:
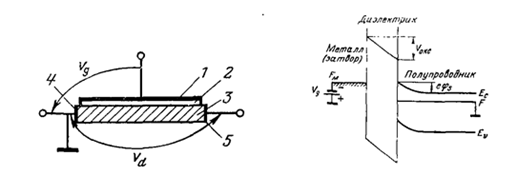 Рисунок 3 – МДП-структура. Рисунок 4 – Энергетическая диаграмма.
Рисунок 3 – МДП-структура. Рисунок 4 – Энергетическая диаграмма.
1 – металлический электрод (затвор),
2 – диэлектрик, 3 – полупроводник,
4 – омический контакт (исток),
5 – омический контакт (сток).
В простейшем случае, когда контактной разностью потенциалов между металлом и полупроводником можно пренебречь в сравнении с Vg, а на границе раздела полупроводник — диэлектрик и в объеме диэлектрика отсутствуют состояния, способные захватить носители заряда, весь индуцированный заряд будет участвовать в создании дополнительной проводимости. Тогда можно записать:
Из соотношения (9) можно найти φs, соответствующий
данному значению Vg, и, следовательно, значение Gs в функции Ys. При выполнении вышеуказанных условий экспериментальная кривая Gs (Vg) дает возможность при известном знаке Vg однозначно определить значение электростатического потенциала.
В опытах по эффекту поля обычно стремятся выполнить условие Сокс << Csp, что дает возможность величину индуцированного заряда определять как Qинд = Сокс Vg (т. е. Vg >> φs) и экспериментальную зависимость строить в координатах Gs (Qинд). Теоретическая зависимость в тех же координатах при известных подвижностях электронов и дырок и уровне легирования полупроводника легко строится по схеме
Реально наблюдаемая в экспериментах по эффекту поля зависимость поверхностной проводимости от индуцированного заряда существенно отличается от теоретической. Причины этого состоят в следующем: 1) между полупроводником и металлом существует контактная разность потенциала qφк = Фм—Фп; 2) на границе раздела полупроводник — диэлектрик и в самом диэлектрике практически всегда существуют состояния, способные нести нескомпенсированный заряд определенного знака и не меняющие своего зарядового состояния при всех достижимых в данном эксперименте значениях поверхностного электростатического потенциала Ys; 3) имеются такие состояния, заполнение которых электронами зависит от значения Ys. Первые две из указанных причин приводят к тому, что в полупроводнике существует поверхностная проводимость (Gs =1) в отсутствие напряжения на металлическом электроде (Vq = 0) и, следовательно, происходит параллельный сдвиг экспериментальной кривой Gs (Qинд) относительно теоретической вдоль оси зарядов на величину Qs0. Влияние третьей из указанных причин приводит к гораздо более существенной деформации экспериментальной кривой: кроме сдвига наблюдается изменение формы кривой (рисунок 5).
Таким образом, количественное и качественное различие между теоретической и экспериментальной кривыми поверхностной проводимости от индуцированного заряда позволяет судить о концентрации и энергетическом спектре
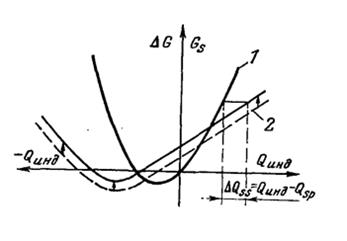
Рисунок 5 – Кривые зависимости поверхностной проводимости от индуцированного заряда.
1 – Теоретическая
2 – Экспериментальная
поверхностных состояний в структуре полупроводник — диэлектрик.
Это обычно и является основной задачей метода эффекта поля. При наличии поверхностных состояний лишь часть индуцированного в полупроводник заряда Qsp участвует в создании поверхностной проводимости, другая часть, т. е. Qss, захватывается на поверхностные состояния:
где знак минус во 2-м слагаемом относится к акцепторным, плюс — к донорным состояниям.
Дата добавления: 2015-04-05; просмотров: 1178;
