Анализ рекурсивных алгоритмов

При изучении темы "Рекурсия" полезно проанализировать рекурсивные алгоритмы с точки зрения последовательности их выполнения. Под последовательностью выполненного рекурсивного алгоритма будем понимать последовательность вызовов алгоритма с различными значениями аргументов и очередью определения результатов.

Рассмотрим сначала функцию расчетов факториала числа (см. выше)

Для алгоритма определения 5-го члена ряда Фибоначчи схема нахождения изображена на рисунке:

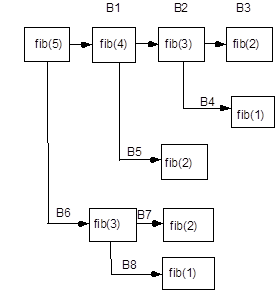
Чтобы определить значение 5-го элемента Фибоначчи, для этого необходимо определить значения fib(2), fib (1), fib (3), fib (2). Из схемы видно также , что в рассматриваемом случае значения fib (1), fib (3), fib (2) определяются дважды. При нахождении члена последовательности с большим номером число повторных вычислений значительно увеличивается. В результате при определения значения fib (17) компьютер выполнит свыше 1000, значения fib (31) свыше 1000000, значения fib (45) свыше 1000000000 операций сложения. В тоже время при использовании не рекурсивного алгоритма для вычисления 45-го члена потребуется всего 43 операции сложения.

Это позволяет сделать вывод о неэффективности использования рекурсии для решения рассматриваемой задачи. Аналогичный вывод можно сделать для решения других задач.