Годовое движение Солнца для широт умеренного пояса

Солнце восходит и заходит в течение года, так как δ < 90° – φ всегда.
Разница в продолжительности дня и ночи в течении года более заметна.
В зените Солнце не бывает, поскольку не может быть δ = φ.
Меридиональная высота Солнца всегда меньше, чем в те же даты в тропическом поясе.
В суточном движении Солнце пересекает I вертикал и в течение дня бывает во всех четвертях горизонта при одноименных φ и δ. При разноименных δ и φ Солнце бывает только в двух четвертях, первая буква наименования которых разноименна с φ.

Для наблюдателя в тропическом поясе 0° < φ < 23°27′N (S).

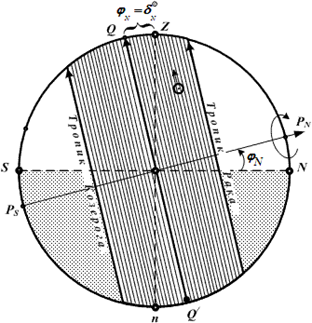
Годовое движение Солнца для φ < 23°27′N (S)

Солнце восходит и заходит ежедневно, так как δ < 90° – φ.
Продолжительность дня и ночи изменяются незначительно.
Дважды в год Солнце в полдень проходит через зенит, когда δ = φ и они одноименны. Если наблюдатель находится на одном из тропиков, то Солнце в зените бывает один раз в году (21.6 – тропик Рака, 21.12 – тропик Козерога).
При δ < φ и одноименных Солнце в суточном движении пересекает I вертикал и проходит все четверти горизонта.
При δ > φ и одноименных Солнце наблюдается только в двух четвертях горизонта.
При разноименных φ и δ (независимо от их величин) Солнце также наблюдается только в двух четвертях горизонта.
Вблизи кульминации азимут Солнца (пеленг на него) за короткий промежуток времени меняется очень быстро.
Летом день несколько длиннее, чем зимой.

Для наблюдателя в полярном поясе φ ≥ 66°33′N (S).

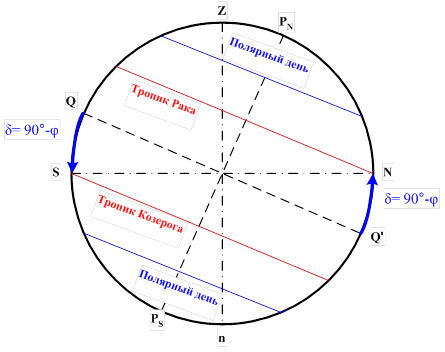
Годовое движение Солнца для φ > 66°33′N (S)

При δ и φ одноименных может наблюдаться незаходящее Солнце, если δ > 90° – φ (полярный день).
При δ и φ разноименных может Солнце не всходить (полярная ночь).
При δ = 90° – φ и одноименных – начало (конец) полярного дня.
При δ = 90° – φ и разноименных – начало (конец) полярной ночи.
Меридиональные высоты и угол падения лучей Солнца еще меньше, чем в умеренном поясе, особенно зимой.
При φ и δ одноименных азимуты Солнца (пеленги на Солнце) в течение суток располагаются во всех четвертях горизонта, при φ и δ разноименных – только в двух.

Дата добавления: 2015-05-13; просмотров: 1645;