Случай с взаимно простыми сомножителями

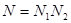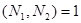Рассмотрим другой крайний случай, когда и . В этом случае существуют целые 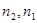, для которых 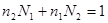. Отсюда следует, что

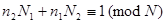(1)

При этом можно считать выполненными неравенства

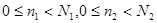.(2)

Если такое неравенство для 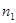, например, не имеет места, можно разделить на 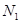. Для

любого целого 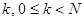из (1) вытекает

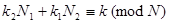. При ограничениях типа (2) 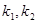находятся однозначно. Имеем

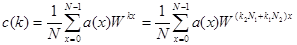. Числа 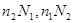- взаимно простые. Следовательно имеем для любого целого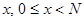

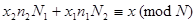. Теперь . Раскрывая скобки и отбрасывая члены кратные 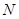, получим показатель вида .

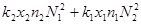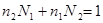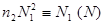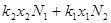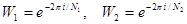Из равенства следует, что , поэтому весь показатель сравним с . Это означает, что . Вводя обозначения , окончательно получим =

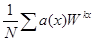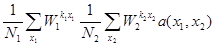. Это означает, что преобразование Фурье для 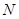точек свелось к последовательному выполнению преобразования Фурье по 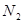точкам, а затем - по 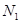точкам результатов предыдущего преобразования. При этом потребуется не более, чем 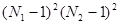умножений. По сравнению с 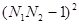выигрыш небольшой. Если же для какого-либо из промежуточных случаев есть своя быстрая схема, выигрыш может получиться значительным.