Взаимное пересечение поверхностей
7.5.1. Пересечение многогранников
Линия пересечения в общем случае является замкнутой пространственной ломаной прямой. Определяется точками пересечения ребер одного многогранника с гранями другого. Точки пересечения ребер с гранями объединяются в звенья. Звено считается видимым, если принадлежит видимым граням. В случае, когда один многогранник – призма, целесообразно на чертеже ее представить в проецирующем положении. Пример построения линии пересечения пирамиды и призмы приведен на рис. 7.21. Так как призма горизонтально проецирующего положения, то на плоскости П1 проекция линии пересечения уже есть, она обозначена точками пересечения ребер пирамиды с гранями призмы – 11, 21, 31 и 41, 51, 61, 71, 81. Линия пересечения в приведенном примере представляет собой два замкнутых контура. Один из них – плоская фигура (треугольник с вершинами, обозначенными точками 1 – 3), второй – прост-ранственный пятиугольник (точки 4 – 8).
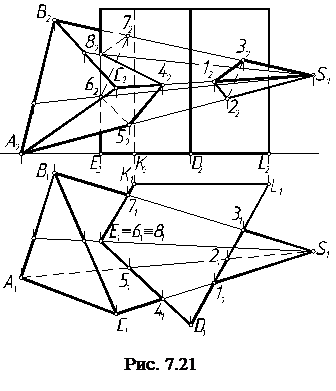 Фронтальные проекции линии пересечения определяются по принадлежности точек 1, 2, 3, 4, 5, 7 ребрам пирамиды, а точек 6 и 8 – граням пирамиды АВ и ВС соответственно, для чего через точки 61 и 81 в этих гранях проводятся прямые l и l'.
Фронтальные проекции линии пересечения определяются по принадлежности точек 1, 2, 3, 4, 5, 7 ребрам пирамиды, а точек 6 и 8 – граням пирамиды АВ и ВС соответственно, для чего через точки 61 и 81 в этих гранях проводятся прямые l и l'.
7.5.2. Пересечение многогранника с криволинейной поверхностью
Линия пересечения в общем случае представляет собой замкнутую пространственную ломаную кривую, которая определяется пересечением граней многогранника с криволинейной поверхностью. Если одна из поверхностей является призмой или цилиндром, то для решения на чертеже их удобно представить в проецирующем положении.
П р и м е р. Дан конус, имеющий призматическое отверстие, образованное четырьмя фронтально проецирующими гранями. Требуется определить линию пересечения (рис. 7.22).
Р е ш е н и е. Так как грани отверстия фронтально проецирующие, то проекция линии пересечения на П2 уже имеется (совпадает с самими проекциями этих граней). Чтобы определить горизонтальную проекцию линии пересечения, 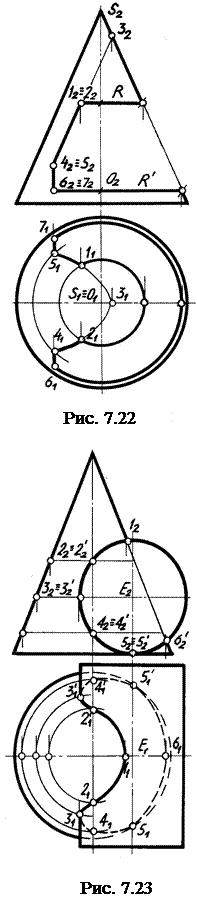 достаточно построить проекции линий от этих четырех граней отверстия. Начнем с верхней грани. Эта грань параллельна основанию кругового конуса, поэтому она его пересекает по части окружности, ограниченной слева точками 1 и 2. Радиус этой дуги по величине соответствует отрезку от осевой конуса до точки на очерковой образующей конуса (R). Вторая грань представляет собой плоскость, пересекающую конус по параболе. Для ее построения достаточно продолжить грань до пересечения с очерковой образующей конуса – получить вершину параболы (точка 3) и определить точки 4 и 5 из условия принадлежности точки поверхности. Пересечение третьей грани с конусом дает часть гиперболы, ограниченную точками 4, 5 и 6, 7. Горизонтальная проекция этой гиперболы будет представлять собой отрезки [41, 51] и
достаточно построить проекции линий от этих четырех граней отверстия. Начнем с верхней грани. Эта грань параллельна основанию кругового конуса, поэтому она его пересекает по части окружности, ограниченной слева точками 1 и 2. Радиус этой дуги по величине соответствует отрезку от осевой конуса до точки на очерковой образующей конуса (R). Вторая грань представляет собой плоскость, пересекающую конус по параболе. Для ее построения достаточно продолжить грань до пересечения с очерковой образующей конуса – получить вершину параболы (точка 3) и определить точки 4 и 5 из условия принадлежности точки поверхности. Пересечение третьей грани с конусом дает часть гиперболы, ограниченную точками 4, 5 и 6, 7. Горизонтальная проекция этой гиперболы будет представлять собой отрезки [41, 51] и
[61, 71].
Четвертая грань параллельна основанию, поэтому горизонтальная проекция линии пересечения проецируется в натуральную величину (частью окружности радиуса R').
Пример построения линии пересечения цилинд-ра и пирамиды приведен в работе [1, с. 54].
7.5.3. Взаимное пересечение криволинейных
поверхностей
Линия пересечения в общем случае – замкнутая пространственная плавная кривая. Она определяется опорными точками (точками, имеющими на чертеже хотя бы по одной проекции), экстремальными (наиболее удаленными), точками смены видимости, при необходимости – промежуточными точками.
П р и м е р. Определить линию пересечения поверхности конуса и цилиндра (рис. 7.23).
Р е ш е н и е. Так как цилиндр является поверхностью фронтально проецирующего положения, то горизонтальная проекция этой линии уже есть, она совпадает с проекцией цилиндра. Проекцию цилиндра на П1 определяем из условия принадлежности точки поверхности. Вначале определим опорные точки – 1, 5, 5', 6, затем – экстремальные – 3, 3', которые будут и точками смены видимости, после этого – промежуточные – 2, 2', 4, 4'. Недостающие проекции экстремальных и промежуточных точек определяем с помощью параллелей, приведенных на поверхности конуса. Пример построения цилиндра и конуса приведен в работе [1, с. 136].
Для некоторых поверхностей, состоящих из конуса и пирамид, линию их пересечения целесообразно определить с помощью “связки” плоскостей. Для этого через вершины этих поверхностей проводят ряд секущих плоскостей, пересекающих поверхности по образующим конуса и по прямым (в гранях пирамиды). Пересечение этих прямых, принадлежащих разным поверхностям, дает общие точки, по которым строят линию пересечения [1, с. 134].
Пересечение цилиндрической и конической поверхностей целесообразно определить с помощью так называемых “вращающихся” вспомогательных плоскостей [1, с. 54]. Линию пересечения эллиптических цилиндров удобно определять с помощью “пучка” параллельных секущих плоскостей [1, с. 138].
8. ОСОБЫЕ СЛУЧАИ ПЕРЕСЕЧЕНИЯ КРИВОЛИНЕЙНЫХ
ПОВЕРХНОСТЕЙ
Ранее было отмечено, что линия пересечения двух криволинейных поверхностей представляет собой пространственную кривую (кривую четвертого порядка). В некоторых случаях эта кривая распадается на плоские кривые (кривые второго порядка). Рассмотрим четыре основных случая.
1. Если две поверхности второго порядка пересекаются в одном месте по плоской кривой, то и в других местах они пересекаются по плоской кривой.
П р и м е р. Даны сфера и эллиптический конус, причем основание конуса вписано в сферу (рис. 8.1).
Р е ш е н и е. Так как основание конуса в этом случае представляет собой плоскую кривую (окружность), то верхняя часть конуса пересекается со сферой по плоской кривой.
2. Если в две пересекающиеся поверхности второго порядка можно вписать сферу, то линия их пересечения представляет собой две плоские кривые.
П р и м е р. Даны цилиндр и конус. Оси поверхностей пересекаются
(рис. 8.2).
Р е ш е н и е. Так как в эти поверхности можно вписать сферу, то линия пересечения будет представлять собой две плоские кривые (два эллипса).

3. Если две пересекающиеся поверхности второго порядка имеют две точки касания, то линия их пересечения распадается на две плоские кривые. Плоские кривые пересекаются между собой в точках касания поверхностей.
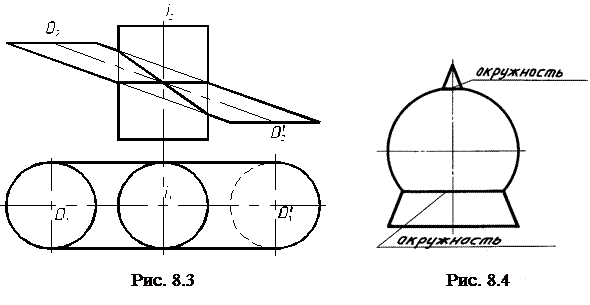 П р и м е р. Даны два цилиндра (круговой и эллиптический) (рис. 8.3).
П р и м е р. Даны два цилиндра (круговой и эллиптический) (рис. 8.3).
Р е ш е н и е. Так как поверхности имеют две точки касания, то линия пересечения будет представлять собой две плоские кривые (в данном случае – окружность и эллипс).
4. Сфера, пересекаясь с соосной поверхностью вращения (поверхности соосные, если имеют общую ось вращения), в пересечении дает окружности. Число этих окружностей соответствует количеству пересечений поверхности сферой (рис. 8.4).
На основании этого свойства сферу можно принимать в качестве посредника при определении линии пересечения некоторых поверхностей.
Дата добавления: 2015-04-29; просмотров: 2198;
