Растровая (ячеистая) модель данных

Ячеистые модели описывают непрерывные поля данных (рельеф, фотоснимки местности и т.д.). В ячеистых моделях участки территории неразрывно разбиваются на одинаковые (регулярные) фрагменты или различные нерегулярные фрагменты (треугольники в нерегулярной триангуляционной модели).

Каждой ячейке в регулярной модели сопоставляется определенный код (число, код цвета и т.д.)

Триангуляционная модель данных (нерегулярная триангуляционная сеть, TIN) предназначена для описания поверхностей. В качестве моделируемой поверхности может выступать рельеф земной поверхности (рис. 3.8) или распределение какого-то параметра по земной поверхности, например, загрязнения окружающей среды, количества выпадающих осадков или среднегодовой температуры.

Для моделирования поверхностей может использоваться и растровая модель, когда в каждом пикселе растра задается высота моделируемой поверхности. Однако триангуляционная модель имеет ряд преимуществ по сравнению с растровой:

- более высокая точность моделирования,

- меньшие затраты памяти,

- возможность в явном виде представлять резкие изломы поверхности, т.е. точки и линии, вдоль которых резко меняется кривизна поверхности (вершины гор, границы оврагов, обрывы рек, границы искусственных сооружений). В растровой модели предполагается, что вся моделируемая поверхность является гладкой поверхностью.

Рис. 3.8. Триангуляционная модель поверхности Земли

Исходными данными для построения триангуляционной модели поверхности служат высотные отметки, изолинии (горизонтали на карте), а также различные структурные линии, меняющие форму поверхности.

В основе триангуляционной модели данных лежит триангуляция– особая структура данных из вычислительной геометрии, определенная на плоскости.

Триангуляция может быть различного вида. В триангуляционной модели данных часто используется так называемая триангуляция Делоне, в которой треугольники строятся так, чтобы они были «максимально равносторонними», а точнее так, что внутрь окружности, описанной вокруг любого треугольника, по возможности не должны попадать узлы триангуляции (рис. 3.9).

Так как триангуляция определена на плоскости, то для моделирования поверхностей в каждом узле триангуляции дополнительно добавляется еще одна координата – высотная отметка. При этом поверхность как бы «вытягивается из плоскости».

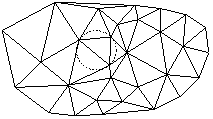
Рис. 3.9. Пример триангуляции Делоне

Сравнительная характеристика векторных и растровых моделей.