Выравнивание рядов динамики.
При исследовании рядов динамики одной из важнейших задач является определение основной тенденции развития явления (тренда) и сглаживание случайных колебаний. С этой целью используются следующие методы выравнивания рядов динамики:
1)метод укрупнения интервалов;
2)метод скользящей средней;
3) аналитическое выравнивание рядов динамики.
Метод укрупнения интервалов основан на том, что первоначальный ряд динамики заменяется другим, уровни которого относятся к большим по продолжительности периодам времени. Средние, исчисленные по укрупненным интервалам, позволяют выявлять направление и характер основной тенденции развития.
Суть метода скользящей средней заключается в том, что для первоначального ряда динамики формируются увеличенные интервалы, состоящие из одинакового количества уровней. Каждый последующий интервал получается смещением от начального на один уровень. В каждом укрупненном интервале скольжения рассчитывается средний уровень, который относится к середине этого интервала. В результате этого получается новый ряд из скользящих средних, позволяющий выявить тенденцию развития явления.
Смысл метода аналитического выравнивания состоит в замене фактических уровней ряда динамики сглаженными, рассчитанными по соответствующей математической функции.
Рассмотрим сущность данного метода на примере выравнивания по прямой.
Уравнение прямой имеет следующий вид:
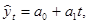
где 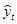 – выравненные уровни ряда динамики, освобожденные от случайных отклонений;
– выравненные уровни ряда динамики, освобожденные от случайных отклонений;
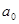 ,
, 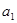 – параметры, определяющие конкретный вид уравнения прямой;
– параметры, определяющие конкретный вид уравнения прямой;
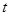 – время.
– время.
Параметры 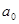 и
и 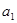 находятся решением системы нормальных уравнений, составленных с использованием метода наименьших квадратов:
находятся решением системы нормальных уравнений, составленных с использованием метода наименьших квадратов:
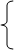
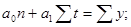
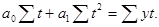
Расчет параметров прямой можно упростить, если отсчет времени 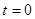 осуществлять с середины ряда динамики. Тогда значения
осуществлять с середины ряда динамики. Тогда значения 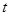 , расположенные до середины, будут отрицательными, а после середины – положительными. В этом случае сумма значений времени
, расположенные до середины, будут отрицательными, а после середины – положительными. В этом случае сумма значений времени 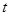 будет равна нулю.
будет равна нулю.
При условии, что 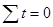 , система нормальных уравнений упрощается, приобретая следующий вид:
, система нормальных уравнений упрощается, приобретая следующий вид:
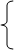
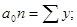
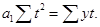
Откуда 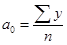 ;
; 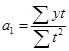 .
.
Аналитическое выравнивание может быть использовано при прогнозировании статистических показателей путем экстраполяции, т. е. нахождения уровней за пределами данного ряда динамики.
Дата добавления: 2015-05-13; просмотров: 1387;
