Второе начало термодинамики. Первое начало термодинамики, выражая закон сохранения и превращения энергии, не позволяет установить направление протекания термодинамических процессов
Первое начало термодинамики, выражая закон сохранения и превращения энергии, не позволяет установить направление протекания термодинамических процессов. Кроме того, можно представить множество процессов, не противоречащих первому началу, в которых энергия сохраняется, а в природе они не осуществляются. Появление второго начала термодинамики - необходимость дать ответ на вопрос, какие процессы в природе возможны, а какие нет - определяет направление развития процессов.
Используя понятие энтропии и неравенство Клаузиуса, второе начало термодинамики можно сформулировать как закон возрастания энтропии замкнутой системы при необратимых процессах: любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает.
Можно дать наиболее краткую формулировку второго начала термодинамики: в процессах, происходящих в замкнутой системе, энтропия не убывает. Здесь существенно, что речь идет о замкнутых системах, так как в незамкнутых системах энтропия может вести себя любым образом (убывать, возрастать, оставаться постоянной). Кроме того, отметим еще раз, что энтропия остается постоянной в замкнутой системе при обратимых процессах. При необратимых процессах в замкнутой системе энтропия всегда возрастает.
2.10 Тепловые двигатели и холодильные машины.
Цикл Карно и его коэффициент полезного действия
для идеального газа.
Изформулировки второго начала термодинамики по Кельвину следует, что вечныи двигатель второго рода – периодически действующий двигатель, совершающий работу за счет охлаждения одного источника теплоты, - невозможен. Для иллюстрации этого положения рассмотрим работу теплового двигателя.
Принцип действия теплового двигателя приведен на рис.63. От термостата с более высокой температурой T1, называемого нагревателем за цикл отнимается количество теплоты Q1, а термостату с более низкой температурой Т2, называемому холодильником, за цикл передается количество теплоты Q2, при этом совершается работа A=Q1 –Q2.
Чтобы термический коэффициент полезного действия теплового двигателя был h =1, должно быть выполнено условие Q2 =0, т.е. тепловой двигатель должен иметь один источник теплоты, а это невозможно. Так, французский физик и инженер Н. Л. С. Карно показал, что для работы теплового двигателя необходимо не менее двух источников теплоты с различными температурами, иначе это противоречило бы второму началу термодинамики.
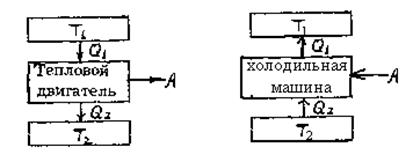
Рис. 2.10.1 Рис. 2.10.2
Процесс, обратный происходящему в тепловом двигателе, используется в холодильной машине, принцип действия которой представлен на
рис. 2.10.2.
Системой за цикл от термостата с более низкой температурой Т2 отнимается количество теплоты Q2 и отдается термостату с более высокой температурой T1 количество теплоты Q1. Для кругового процесса Q=A, но, по условию, Q=Q2 –Q1 <0, поэтому А<0 и Q2 –Q1 = -А, или Q1 =Q2 +А, т.е. количество теплоты Q1, отданное системой источнику теплоты при более высокой температуре T1, больше количества теплоты Q2, полученного от источника теплоты при более низкой температуре Т2, на величину работы, совершенной над системой. Следовательно, без совершения работы нельзя отбирать теплоту от менее нагретого тела и отдавать ее более нагретому. Это утверждение есть не что
иное, как второе начало термодинамики в формулировке Клаузиуса.
Однако второе начало термодинамики не следует представлять так, что оно совсем запрещает переход теплоты от менее нагретого тела к более нагретому. Ведь именно такой переход осуществляется в холодильной машине. Но при этом надо помнить, что внешние силы совершают работу над системой, т.е. этот переход не является единственным результатом процесса.
Основываясь на втором начале термодинамики, К а р н о вывел теорему носящую теперь его имя: из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей (Т1) и холодильников (Т2), наибольшим кпд обладают обратимые машины; при этом кпд обратимых машин, работающих при одинаковых температурах нагревателей (Т1) и холодильников (Т2), равны друг другу и не зависят от природы рабочего тела.
Карно теоретически проанализировал обратимый наиболее экономичный цикл, состоящий из двух изотерм и двух адиабат, и называемый
циклом Карно. Рассмотрим прямой цикл Карно, в котором в качестве рабочего тела используется идеальный газ, заключенный в сосуд с подвижным поршнем.
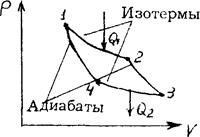 рис. 2.10.3
рис. 2.10.3
| Цикл Карно изображен на рис. 2.10.3, где изотермические расширение и сжатие заданы соответственно кривыми 1-2 и 3-4, а адиабатические расширение и сжатие - кривыми 2-3 и 4-1. |
При изотермическом процессе U=const, поэтому количество теплоты Q1, полученное газом от нагревателя, равно работе расширения А12, совершаемой газом при переходе из состояния 1 в состояние 2:
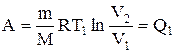 . (2.10.1)
. (2.10.1)
При адиабатическом расширении 2-3 теплообмен с окружающей средой отсутствует, и работа расширения А23 совершается за счет изменения внутренней энергии:
 .
.
Количество теплоты Q2, отданное газом холодильнику при изотермическом сжатии, равно А34
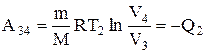 . (2.10.2)
. (2.10.2)
Работа адиабатического сжатия
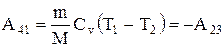 .
.
Работа, совершаемая в результате кругового процесса,
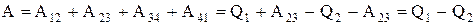
и, как можно показать, определяется площадью, выполненной на рис. 2.10.3.
Термический кпд цикла Карно
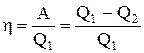 .
.
Применив уравнение для адиабат 2-3 и 4-1, получим
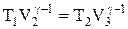 ,
, 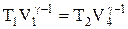 , (2.10.3)
, (2.10.3)
откуда
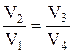 .
.
Далее получим
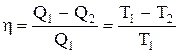 , (2.10.4)
, (2.10.4)
т.е. для цикла Карно кпд действительно определяется только температурами нагревателя и холодильника. Для его повышения необходимо увеличивать разность температур нагревателя и холодильника. Например, при Т=400 К и Т=300 К h=0,25. Если же температуру нагревателя повысить на 100 К, а температуру холодильника понизить на 50 К, то h=0,5. Кпд всякого реального теплового двигателя из-за трения и неизбежных тепловых потерь гораздо меньше вычисленного для цикла Карно.
Дата добавления: 2015-06-01; просмотров: 849;
