Кластерный анализ

В любой научной деятельности классификация является одной из фундаментальных составляющих, без которой невозможны построение и проверка научных гипотез и теорий. В качестве метода типологического анализа наиболее широко в настоящее время используется кластерный анализ – это обобщенное название достаточно большого набора алгоритмов, используемых при создании классификации. Сам термин “кластерный анализ” впервые был предложен Р. Трионом [Tryon, 1939], а слово "cluster" переводится с английского языка как "гроздь, кисть, пучок, группа" (по этой причине первое время этот вид анализа называли "гроздевым анализом").

Теоретическим введением в использование методов кластеризации в биологии явилась книга "Принципы численной таксономии", опубликованная двумя биологами – Р. Сокэлом и П. Снитом [Sokal, Sneath, 1963]. Авторы этой книги исходили из того, что для создания эффективных биологических классификаций процедура кластеризации должна обеспечивать использование всевозможных показателей, характеризующих исследуемые экосистемы, производить оценку степени сходства между отдельными организмами и обеспечивать размещение схожих объектов в одну и ту же группу. При этом сформированные группы должны быть достаточно "локальны", т.е. сходство объектов (организмов) внутри групп должно превосходить сходство групп между собой. Последующий анализ выделенных группировок, по мнению авторов, может выяснить, отвечают ли эти группы разным биологическим видам. Иными словами, Сокэл и Снит предполагали, что выявление структуры распределения объектов в группы помогает установить процесс образования этих структур. А различие и сходство организмов разных кластеров (групп) могут служить базой для осмысления происходившего эволюционного процесса и выяснения его механизма.

Определение кластерного анализа дано, например, в последнем издании "Статистического словаря" [1989]: “Кластерный анализ – совокупность математических методов, предназначенных для формирования относительно "отдаленных" друг от друга групп "близких" между собой объектов по информации о расстояниях или связях (мерах близости) между ними. По смыслу аналогичен терминам: автоматическая классификация, разбиение, группировка, таксономия, распознавание образов без учителя”.

Под кластером обычно понимается группа объектов [Дидэ, 1985], обладающих свойством метрической близости ("сходности"): плотность объектов внутри кластера больше, чем вне его.

Абсолютное большинство методов кластеризации [Дюран, Оделл, 1980; Классификация и кластер.., 1980; Мандель, 1988] основывается на анализе квадратной и симметричной относительно главной диагонали матрицы коэффициентов сходства (расстояния, сопряженности, корреляции и т.д.). При определении корреляции между признаками сравнивается распределение двух каких-либо видов в определенной серии наблюдений и оценивается, насколько тесно совпадают эти распределения. Определение корреляции между объектами представляет обратную задачу: сравниваются две точки отбора проб и оценивается, насколько тесно совпадает набор их признаков. В кластерном анализе всегда подчеркивалась принципиальная равноправность обоих этих методов.

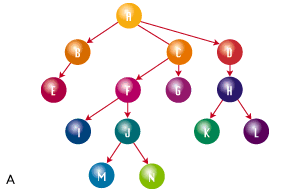
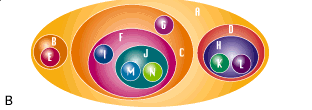
Наиболее часто используются иерархические классификации [Айвазян с соавт., 1974; Жамбю, 1988], которые могут быть представлены в двух основных формах – дерева (фиг. А рис. 2.3) и вложенного множества (фиг. В). Дерево представляет собой специальный вид направленного графа – структуры, состоящей из узлов, связанных дугами. Дерево иерархической классификации обладает следующими свойствами:

· имеется один и только один корень (иногда в полном противоречии с ботаникой его называют вершиной);

· всегда имеется путь от корня до любого другого узла в дереве;

· каждый узел, кроме корня, имеет одного и только одного родителя (т.е. граф не должен иметь циклов и петлей) и произвольное число потомков;

· узлы дерева, которые не имеют потомков, называются листьями и они соответствуют исходному множеству классифицируемых объектов.

Рис. 2. Методы представления результатов классификации

(А – дерево, В – вложенное множество)

Визуализация дерева разбиений осуществляется в виде двух специальных графиков:

· дендрограммы, где пары объектов соединяются в соответствии с уровнем связи, отложенным по оси ординат,

· дендрита – графа максимального корреляционного пути, где изображение объектов на плоскости произвольно, а ребра соответствуют максимальному значению из всех связей каждого объекта с другими.

В справочнике И.П. Гайдышева [2001] показано, что дендрограмма, и дендрит – визуальное отображение одной и той же сущности: по графу легко может быть построена дендрограмма и наоборот.

Многомерный подход основан на предположении, что существует возможность лаконичного объяснения природы анализируемой многокомпонентной структуры [Браверман, Мучник, 1983; Александров, Горский, 1983; Верхаген с соавт., 1985]. Это означает, что есть небольшое число определяющих факторов, с помощью которых могут быть достаточно точно описаны как наблюдаемые характеристики анализируемых состояний, так и характер связей между ними [Ким с соавт., 1989]. Иногда эти факторы могут оказаться в явном виде среди исследуемых признаков, но чаще всего оказываются латентными или скрытыми. Сжатое (редуцированное) представление исходных данных в виде матрицы Fс меньшим числом переменных p (m > p) без существенной потери информации, содержащейся в исходной матрице X, является сущностью таких важнейших методов снижения размерности, как факторный анализ, многомерное шкалирование, метод главных компонент, целенаправленное проецирование [Ватанабе, 1969; Харман, 1972; Дубров, 1978; Терехина, 1986; Краскел, 1986; Дэйвисон, 1988; Ципилева, 1989]. Эти методы применяются при решении следующих задач:

· редукция данных или понижение размерности признакового пространства типа "объект-признак" за счет сведения многочисленных взаимозависимых наблюдаемых переменных к некоторым обобщенным ненаблюдаемым факторам;

· преобразование исходных переменных к более удобному для визуализации виду и классификация объектов на основе сжатого признакового пространства;

· создание структурной теории исследования объектов и интерпретация косвенных факторов, не поддающихся непосредственному измерению.

С общетеоретических позиций кластерный анализ также является своеобразным методом снижения размерности, выполняемый в пространстве объектов. Определены [Попечителев, Романов, 1985] основные требования, которые являются определяющими для выбора метода снижения размерности: взаимная некоррелированность, наименьшие искажения структуры моделируемых данных, наибольшая надежность правильного разбиения исходной выборки на естественные группы и т.д.