Статические методы исследования данных

Возникает вопрос: существует ли взаимосвязь между различными перемен­ными экосистемы. Ответ можно получить посредством регрес­сионного или корреляционного анализа в зависимости от цели задачи. Вид связи между переменными выражается регрессионным уравнением, а ее интенсивность — с помощью корреляции.

Регрессия и корреляция. Регрессионный анализ необходим для ре­шения задач, в которых стохастические зависимости (стохастические отноше­ния «причина — следствие») описываются функциями с одной или нескольки­ми переменными, определяемыми как независимые.

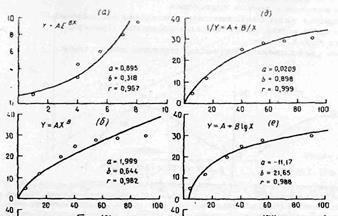
Простая регрессия с одной независимой переменной х и одной зависимой переменной .у может быть линейной или нелинейной. Обычно нелинейные ре­грессии (рис. 1) можно получить с помощью линеаризации (преобразования переменных) и упрошенных вычислительных методов. Этот подход может от­рицательно сказаться на качестве аппроксимации. Методы оце­нивания дают так называемые несмещенные оценки. В тех случаях, когда ни одну из переменных нельзя считать зависимой, для стати­стического описания более всего подходят такие методы, как линия наилучше­го приближения Бартлетта или геометрическое среднее. В основе метода гео­метрического среднего лежит усреднение наклонов линейных регрессий у = f(x) и x = f (v), и то время как линия наилучшего приближения Бартлетта строится на основе оценочных данных подвыборки.

Множественная регрессия имеет одну зависимую и несколько независимых переменных. Наиболее часто используются линейные уравнения.

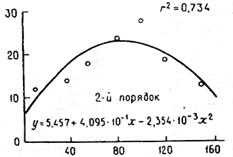
Во многих ситуациях для описания экологических процессов или систем используются полиномы n-го порядка{полиномиальные регрессии) (рис. 1.).

Самая высокая степень п выражает порядок полинома. Если используются полиномы высоких порядков, то возникает вопрос о возможности интерпре­тации переменных в степени. Для некоторых переменных, имеющих наивысшуюую степень третьего порядка, возможна вполне обоснованная физическая ин­терпретация (например, насыщение растворенным кислородом / (T_w) можно выразить в виде полинома третьего порядка. Однако в большинст­ве случаев полиномы служат лишь для описания взаимосвязей.

В результате замены переменных х функциями синуса и косинуса получаем уравнение:

у = а + b₁sinх + b₂cosх.

Оно представляет собой простейший вид периодической регрессии, или так называемого полинома Фурье. В более широком смысле этот метод называ­йся анализом Фурье

Этот вид регрессии часто используется для определения периодической на­правленности изменений, когда проводится анализ данных измерений качества воды, воздуха и т.д.

РИС. 1. Регрессия полиномами 2 порядка (2-7-го порядков). Для каждого порядка используется од­на и та же система точек. Возрастание порядка сопровождается увеличением показателя эффективности г2 до тех пор, пока кривая не пройдет через все точки (г2 = I). Высшие по­рядки могут сопровождаться отрицательными модельными результатами, которые не со­гласуются с действительностью (например, как в 7-м порядке). Значения модельных пара­метров резко уменьшаются по мере возрастания порядка.
Нелинейные регрессии

Корреляционный анализ применяется с целью установления степени корре­ляции между двумя или большим числом стохастических переменных, а также для определения степени стохастической зависимости, существующей между ними. Последняя может быть описана с помощью коэффици­ентов корреляции. Двусторонние и многосторонние зависимости описывают­ся простыми коэффициентами, а также коэффициентами частной и мно­жественной корреляции. Коэффициент частной корреляции также необходим при выборе переменных, оказывающих влияние на экосистему. Если предполагается многомерное нормальное распределение, то оно будет служить мерой линейной зависимости двух случайных переменных х_j и х_k при устранении влияния всех остальных случайных переменных. Квадрат коэффициента корреляции называ­ется коэффициентом детерминации R².

Дисперсионный и ковариационный анализы. Дисперсионный ана­лиз (AOV) представляет собой способ качественного и количественного изуче­ния влияния одной или нескольких переменных на результаты эксперимента. В тех моделях, где это влияние имеет фиксированный характер, обычно сравниваются лишь средние значения нескольких случайных выборок. Однако в моделях, учитывающих случайные эффекты, сами влияющие факторы рас­сматриваются как случайные выборки из множества возможных появлений этих факторов. Такая же картина может иметь место при рассмотрении не­прерывно контролируемых качественных параметров воды.

Ковариационный анализ можно использовать при количественном изуче­нии различной степени воздействия одной или нескольких переменных на экс­периментальные данные, и при этом обязательно учитывается влияние допол­нительных случайных переменных. По существу этот метод позволяет объединить дисперсионный и регрессионный анализы, каждый из которых относится к моделям с фиксированными воздействиями.

Дискриминантный и факторный анализы. Дискриминантный анализ применяется для разделения или классификации объектов и их связи с двумя и более совокупностями (группами, популяциями). Фактически он представляет собой способ разделения. Последнее выполняется на основе анализа количественных характеристик и учета дискриминантной (разделительной) функции, с которой связано принятие решения о проведении классификации.

Факторный анализ используется для изучения соотношений между случай­ными переменными, обусловленных общими причинами, или факторами, а также с целью вывода этих соотношений. При этом особое внимание уделяется точечному оцениванию параметров.

Методы дискриминантного и факторного анализов были разработаны в общей экологии и фитоэкологии высших растений с целью типизации пространственно-временных отношений различных видов и переменных окру­жающей среды. В результате информация о различ­ных биологических видах или переменных окружающей среды, представляю­щих собой кластеры в пространстве и времени, поступает одновременно. Это обстоятельство является отправной точкой, от которой начинается использо­вание кластерного анализа для обнаружения источников загрязнения потоков. Этот же метод применен в для определения взаимосвязи между пе­ременными трофического состояния.

Методы оценки параметров. Обычно очень трудно получить пара­метры модели из реальной системы. Поэтому они оцениваются исходя из дан­ных наблюдений за различными переменными и их выборочных статистиче­ских функций. Это могут быть точечные оценки или оценки на интервалах, в зависимости от того, определяется ли сам параметр или интервал, в котором он находится. Подобные оценки удобно получать с помощью статисти­ческих компьютерных пакетов программ. Для полу­чения нелинейной оценки (простых) функций существует несколько способов – алгоритм Гаусса — Зайделя, алгоритм Ньютона — Рафсона, ме­тод Маркварта и др

Чтобы получить неизвестный параметр а на основе данных измерений, а затем оценить его, необходимо рассчитать значение g определенной оценоч­ной функции G , распределение которой зависит от а . Значение g использует­ся для оценки а, обозначаемой а. Функция С определяется как оценочная функция неизвестного параметра а.

Методы оценки параметров, в основе которых лежит метод наименьших квадратов, оказались особенно эффективными в экологии. Существу­ют прямые и косвенные методы. Прямые методы (регрессия, марковская оценка, оценка Байеса, оценка максимального правдоподобия) позволяют оценивать параметры в течение одного шага, исходя из массива данных измерений на входе и выходе сигналов из системы. При использовании этих методов могут возникнуть проблемы их применимости на практике ввиду необходимости иметь априорную информа­цию о системе, играющей роль исходной модели. Косвенные методы де­лятся на рекурсивные и нерекурсивные. Рекурсивные методы позволяют под­страивать модель с данной структурой к системе пошаговым способом, при котором каждая новая группа данных измерений дает возможность сделать очередной шаг в подстройке модели. Все параметры должны подвергаться переоценке на протяжении всего процесса