Обобщенный алгоритм построения математической модели
Процедуру построения математической модели реальной системы, процесса или явления можно представить в виде алгоритма. Блок-схема, иллюстрирующая алгоритм построения математической модели, приведена на рис. 4.2.
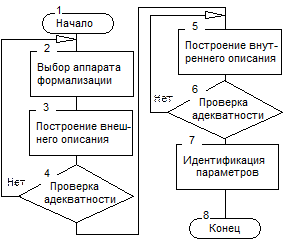
Рис.4.2. Алгоритм построения модели системы
Основные этапы построения математической модели.
1. Выделение системы из внешней среды. Выделение связей с внешней средой, разбиение множества связей на входные и выходные параметры. Наблюдение за системой, накопление информации, достаточной для выдвижения гипотез о структуре системы и ее функционировании.
2. Выбор аппарата формализации осуществляется исследователем и зависит от многих факторов, в частности - от целей моделирования, имеющейся информации, полученных экспериментальных данных.
3. Построение внешнего описания сводится к поиску области определения (в пространстве входных воздействий) и области значений (в пространстве выхода), размерность которых была определена на этапе 1, и определении соответствия между входными и выходными параметрами.
4,6. Если проверка адекватности показывает, что построенная модель не удовлетворяет предъявляемым к ней требованиям и причиной этого является более сложный характер поведения системы, то производится выбор нового метода математического описания.
5. В случае удачного построенного внешнего описания производится переход к внутреннему описанию, при этом размерность пространства состояний системы (то есть размерность вектора 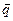 ) должна быть минимальной.
) должна быть минимальной.
7. Определение (идентификация) качественных и количественных характеристик параметров, определяющих функционирование системы.
Среди представленных этапов построения математической модели методы идентификации параметров наиболее хорошо разработаны. При их использовании предполагается, что структура системы известна, а неизвестны только значения параметров. Задача параметрической идентификации в этом случае сводится к поиску значений параметров, обеспечивающих минимизацию некоторой функции ошибки. Особое значение на всех этапах построения математической модели является проверка адекватности, непротиворечивости модели и ее достаточности для реализации целей исследования.
Если построенная модель недостаточно полно отражает свойства моделируемой системы, то никакое применение самых современных средств и методов исследования не может дать удовлетворительных результатов. Таково неизбежное свойство использования математической модели. Все получаемые при ее исследовании результаты отражают свойства собственно модели, а не исходной системы, для исследования которой модель была разработана. После того, как модель построена, она начинает «жить своей собственной жизнью».
Контрольные вопросы
1. Что представляет собой модель?
2. Опишите схему абстрактной модели.
3. Что относится к входным параметрам системы?
4. Что относится к выходным параметрам системы?
5. Что характеризуют параметры состояния системы?
6. Назовите виды моделирования, опишите их.
7. Опишите два подхода к построению математической модели.
8. Опишите процедуру построения математической модели реальной системы.
Тема№5
Оценка сложных систем
Основные типы шкал измерения
Дата добавления: 2015-05-08; просмотров: 1329;
