Мышления учащихся

Прежде всего необходимо выстроить схему решения задач и совместно разобрать ее на одном примере, который приводится в тексте рекомендаций (задача: «Какое число самое большое из следующих..?»). Остальные примеры учащиеся должны разобрать дома самостоятельно. После правильного анализа каждой задачи необходимо предложить им самим найти другие, аналогичные и проанализировать их по уже выработанному плану. Кроме того, следует посоветовать учащимся подобрать такие задачи, в которых нужно не вычислять конечный результат, а лишь отработать и описать план решения, нахождения того, что требуется по условию. При этом можно предложить учащимся продумывать и описывать два разных плана решения одной и той же задачи: один – более сложный и трудоемкий, а другой – более простой и краткий.

Целесообразно устраивать своеобразные конкурсы: кто придумает больше разных планов решения какой-либо задачи (специально подобранной так, чтобы были возможны разные планы); кто придумает такой план решения, который годится для большого числа задач; кто придумает самый простой план.

Для тренировки умения обдумывать способ решения можно давать учащимся после получения ответа на задачу задание описать ход решения, характер затруднений, указать, где еще можно использовать найденный ими способ.

Поскольку работа над решением задач – процесс очень длительный, то ее итоги целесообразно подводить лишь в конце года, чтобы наметить новые возможности для совершенствования умения думать.

Рекомендации ученикам.Каждый из вас, проучившись в школе не один год, успел, конечно, заметить, что некоторые ребята хорошо решают задачи, а другие – не очень. И часто можно слышать, как про первых говорят: «Толковые, сообразительные!» А про других... Впрочем, что говорят про других, можно и так догадаться.

Ясно, что каждому хочется, чтобы его называли умным, понятливым, сообразительным. Но можно ли стать сообразительнее? Можно ли научиться решать задачи лучше, быстрее? Конечно да, если постоянно тренироваться.

Как же тренироваться, какие умения нужно освоить, чтобы хорошо решать задачи? Психологи много наблюдали за тем, как решают задачи сообразительные ученики. И пришли к выводу, что есть три основных умения, которые помогают при столкновении с самыми разными задачами: и учебными, школьными, и неучебными, занимательными.

Во-первых, это умение разбираться в задаче, в том, что дано в ее условии и что нужно получить.

Во-вторых, это умение планировать решение, продумывать варианты действий и их последовательность.

В-третьих, это умение осознавать способ уже решенной задачи, обосновывать его правильность, осмысливать возможности его применения в других случаях.

Посмотрим, как пользовался этими умениями сообразительный ученик, когда решал такую задачу: «Какое число самое большое из следующих:

199878227 4582 245741010 ?»

421312' 31989 ' 85251 ' 96543 ' 76548 '

Прежде всего ученик приступил к разбору условий задачи, внимательно изучал, рассматривал пять имеющихся чисел. В результате он быстро обнаружил, что второе, третье и четвертое числа нет смысла сравнивать – они самые маленькие, меньше одной десятой. Затем, повторив требование, он начал искать пригодные варианты для сравнения первого и пятого чисел: 1) привести эти дроби к общему знаменателю; 2) разделить в этих дробях знаменатель на числитель, 3) разделить числитель на знаменатель, чтобы привести их к виду десятичных дробей.

Но все варианты требовали множества сложных вычислений, и ученик сам признал их неподходящими. Он стал действовать так: упростил первую и последнюю дроби – 19 и 41. После этого ему стало ясно, что последняя дробь больше первой; ее числитель превышает по значению половину знаменателя. Придя к такому выводу, ученик начал думать, почему ему удалось решить задачу правильно. При этом он снова перечитал требование и опять посмотрел данные в ней числа. Потом сформулировал: «Эту задачу можно назвать задачей на сравнение многозначных дробей. Интересно, все ли многозначные дроби сравниваются путем упрощения?»

В поисках ответа он стал придумывать разные многозначные дроби и сравнивать их путем упрощения, сокращения по двузначной дроби. После проделанных опытов ученик пришел к выводу, что способ упрощения многозначных дробей применим в разных случаях.

Нам здесь интересно отметить, что в результате такого обдумывания и проверки способа решения задачи можно не только толково рассказать, но и научить пользоваться им другого человека. Следовательно, этот способ может употребляться осмысленно, сознательно. Завершая анализ решения задачи, мы вправе считать, что теперь у нас есть общее представление о том, как «работают» три основных умения сообразительного ученика и какую роль они выполняют.

Давайте посмотрим теперь, как можно тренировать эти умения, решая разные учебные задачи. Перед нами следующая задача:

«В прямоугольной трапеции основания равны 2 см и 4 см и один из углов равен 45 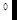'. Вычислить площадь трапеции!»

Прежде чем приступить к решению, нужно разобраться в задаче. Это значит, что ее условно следует разделить на отдельные части, например так:

дано: 1) прямоугольная трапеция,

2) основания трапеции – 2 см и 4 см,

3) один из углов равен 45 '.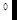

Требуется: вычислить площадь этой трапеции.

Дальше необходимо каждое из трех данных, которые мы выделили в условии, соотнести, сопоставить с требованием. «Вычислить площадь трапеции» означает, что нужно найти такие данные, которые можно подставить в формулу для вычисления площади трапеции: произведение полусуммы оснований на высоту.

Сопоставляя данное «прямоугольная трапеция» с требованием, можно сделать вывод, что в нашем случае одна сторона трапеции является ее высотой.

Сопоставляя данное «основания трапеции 2 см и 4 см» с требованием, можно получить значение части формулы: полусумма этих оснований равна 3 см.

Сопоставление данного третьего пункта с требованием никак не приближает нас к решению задачи, поскольку величина углов формулой не предусматривается.

Тогда попробуем сопоставить данные (1) и (3) между собой. Для этого нарисуем какую-нибудь прямоугольную трапецию. На чертеже сразу видно, что два угла трапеции равны 90 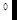, один угол (данное (3) равен 45 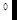и оставшийся угол – тупой – равен, следовательно, 135 .

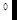Здесь разбор условия задачи кончается, и дальше нужно уже думать над тем, как узнать величину высоты (т. е. одной из сторон) трапеции.

Обратимся к еще одной задаче, тоже геометрической, чтобы потренировать умение разбираться в их условии: «Вычислить площадь четырехугольника, диагонали которого взаимно перпендикулярны и равны 6 см и 8 см».

Теперь, вероятно, вы уже догадались, что сначала нужно разделить условие задачи на отдельные части:

дано: 1) четырехугольник,

2) диагонали четырехугольника,

3) диагонали взаимно перпендикулярны,

4) одна диагональ – 6 см, другая – 8 см.

Требуется: вычислить площадь четырехугольника.

При таком разборе условия хорошо видно: непонятно, какой четырехугольник имеется в виду (параллелограмм, трапеция, прямоугольник или что-нибудь еще). Дальше действуем, как в предыдущем случае: сопоставляем по очереди выделенные данные с требованием задачи. Сразу убеждаемся, что при сравнении данных (1) и (2) с требованием мы ничего нового не получаем. Сопоставляя данное (3) с требованием, начинаем думать, какой же четырехугольник имеет взаимно перпендикулярные диагонали: трапеция не подходит, параллелограмм также, прямоугольник не годится. Тогда из известных нам четырехугольников остается квадрат и ромб. При сопоставлении данного (4) с требованием уточняем: составитель задачи имел в виду только ромб, поскольку у квадрата диагонали не только взаимно перпендикулярны, но и равны.

В результате проведенного разбора, в ходе которого мы сравнили каждое из выделенных данных условий с требованием, удалось узнать, что нужно вычислить не просто площадь четырехугольника, а площадь ромба. На этом разбор заканчивается, и дальше нужно думать, как по известным величинам диагоналей найти по формуле площадь ромба. Конечно, для этого необходим чертеж ромба, нужно продумать и дополнительные построения или просто догадаться, как найти высоту ромба и его основание, произведение которых и составляет его площадь.

Вот так тренируется умение разбираться в задаче, т. е. полезно специально практиковаться в разделении условия задачи на части и в сопоставлении каждой из них отдельно с требованием. Конечно, это не означает, что после разбора любая задача будет решена. Но, по мнению психологов, многие ученики не справляются с решением именно потому, что плохо разбираются в условиях и требованиях: учитывают не все данные, часть информации, заложенной в условие задачи, остается вне поля их внимания.

Итак, если стараться действовать аналогичным образом при решении задач по разным школьным предметам, особенно при выполнении домашних заданий, то в результате вы освоите умение разбираться в задачах. Полезно иногда, не решая, просто просматривать задачи, тренироваться в разборе их условий и требований. Можно тренировать умение планировать свои действия на основе любых школьных задач. Главное, за чем нужно следить,– до вычисления ответа пытаться составить не менее двух разных планов ее решения.

Один из этих планов должен быть более коротким и экономичным, чем другой.

Если вы будете намечать нужные действия до фактического решения задачи, до вычислений, то всегда сможете, не делая грубых ошибок и не затрачивая дополнительного времени, найти успешный план. Когда же вы сразу, без предварительно составленного плана приступаете к решению, тогда ситуация чревата путаницей, и вполне вероятно, что вас ждет неудача, поскольку, не имея плана решения, трудно установить, в какой момент и где произошла ошибка.

И главное, нельзя точно установить, в чем ошибка: в вычислениях или в порядке действий.

Возьмем для примера такую физическую задачу: «Всадник проехал сначала 6 километров за 25 минут и потом 7 километров за 15 минут. После этого он ехал со скоростью 6 км/ч 40 минут и со скоростью 10 км/и 10 минут. В заключение 'своего путешествия он проехал со скоростью 12 км/ч 3 километра и со скоростью 20 км/ч еще 4 километра. Какова средняя скорость всадника за все время движения?»

Общая идея этой задачи, конечно, ясна: нужно опираться на то, что скорость есть расстояние, деленное на время. Однако ход решения здесь может развертываться по-разному.

Один план может включать 15 пунктов, выполняя каждый из которых вы узнаете: 1) скорость передвижения всадника в течение первых 25 минут, 2) скорость за следующие 15 минут, 3) общее время, за которое он проехал первую часть пути, т.е.до того, как начал двигаться со скоростью 6 км/ч, 4) общее расстояние первых двух участков пути, 5) среднюю скорость до этого расстояния, 6) расстояние, которое всадник ехал со скоростью 10 км/ч, 7) общее расстояние, которое он проехал в средней части пути, т. е. до того, как увеличил скорость до 12 км/ч, 8) общее время средней части пути, 9) среднюю скорость этой части пути, 10) время, затраченное на предпоследние 3 километра, 11) время, затраченное на последние 4 километра, 12) общее время, затраченное на последнюю часть пути, т. е. после того, как он увеличил скорость до 12 км/ч, 13) общее расстояние, которое он проехал в последней части пути, 14) среднюю скорость последней части пути, 15) среднюю скорость для всего путешествия.

Другой план проще – он включает 7 пунктов, выполняя каждый из которых нужно узнать: 1) время, затраченное на предпоследние 3 километра, 2) время, затраченное на последние 4 километра, 3) общее время, затраченное на все путешествие, 4) расстояние, пройденное за 40 минут в средней части путешествия, 5) расстояние, пройденное за 10 минут в средней части путешествия, 6) общую протяженность всего путешествия, 7) переднюю скорость для всего путешествия.

Сравнивая оба плана, легко видеть, что второй требует меньше действий. Значит, даже не решая задачу, не вычисляя ответ, можно выбрать нужный план. Для составления планов пригодны два способа: запись на бумаге возможных действий и придумывание в уме, про себя или вслух.

Чтобы научиться разрабатывать планы в уме, без помощи бумаги, нужно практиковаться на решении простых задач, где требуется выполнить лишь несколько действий. Кроме того, задачи полезно сочинять самостоятельно, поскольку, придумывая новую задачу, мы непременно должны проверить, решаема ли она и, если да, то за какое количество действий.

Сопоставление планов в уме поможет еще и потому, что при хорошем развитии этого умения у вас всегда будет возможность быстро найти правильное решение и обдумать свои действия. Вы сможете легко заметить и исправить ошибки еще до начала вычислений. Вам безусловно известно, что умение быстро соображать особенно важно при решении большого числа задач за ограниченное время, например, на контрольных и экзаменах.

И последнее, третье, чем пользуются сообразительные ученики,– умение обдумывать способ уже решенной задачи, чтобы понять, почему ее удалось решить именно этим способом и как его можно обосновать, рассказывая другим. Так же как и предыдущие два умения, третье (обдумывать способ решенной задачи) тренируется на любом учебном материале. Возьмем для примера несложную задачу: «Постройте квадрат, равный по площади данному треугольнику».

Способ решения этой задачи найти, вероятно, нетрудно. Известно, что площадь треугольника равна половине произведения его основания на высоту, а площадь квадрата – произведению его сторон. Поэтому ясно, что равновеликость заданных фигур достигается тогда, когда половина произведения высоты треугольника на его основание будет равна произведению сторон квадрата, которые, как мы знаем, равны. Следовательно, квадрат, равновеликий треугольнику, должен иметь такую сторону, величина которой будет равна корню квадратному из половины произведения высоты треугольника на его основание.

Таков процесс решения этой задачи. В чем же может состоять его обдумывание? Оно заключается в том, чтобы выяснить, насколько этот способ применим при решении похожих задач.

Например, мы задаемся вопросом, как построить параллелограмм, равновеликий треугольнику (прямоугольник, трапецию и т. д.). Пытаясь найти ответ и стараясь при этом использовать уже знакомый нам по предыдущей задаче способ уравнивания площадей фигур, мы и будем тем самым обдумывать его, осмысливать и осознавать, поймем, почему он подходит для нашей и ряда других задач и не годится для остальных.

Итак, мы рассмотрели с вами, как можно развивать три основных умения самостоятельного мышления: разбираться в задаче, планировать ее решение, обдумывать его способ. Главное, что нужно делать для развития этих умений,– регулярно их применять. Только в результате постоянной тренировки, решая разные задачи, эти умения будут хорошо освоены.

Заметим, что эти умения развиваются нетолько при решении школьных задач. Существует множество разнообразных занимательных задач, решение которых поможет вам стать сообразительнее.

Умение разбираться в условии задачи, выделять в нем важные и второстепенные данные развивают такие игры, в которых один человек что-то загадывает, а другой отгадывает, задавая вопросы. По сведениям, которые сообщаются, второй постепенно узнает, что было задано, т.е., задавая не любые, а нужные для разгадки вопросы, отгадчик постоянно уточняет свои знания.

Возьмем, к примеру, игру «Отгадай число». Кто-то загадывает двузначное число, которое составлено из двух разных цифр от 0 до 9, а вы должны отгадать его. Вы задаете вопросы, называя какое-нибудь двузначное число. В ответ вам будет сообщаться, сколько цифр угадано (ни одной, одна или две), а также смогли вы указать места загаданных цифр (ни одного места, одно или, наконец, оба места). Последние сведения связаны с тем, что при загадывании учитывается, на каком месте находится та или иная цифра – десятков (слева) или единиц (справа).

Попробуем сыграть в эту игру, и вы сразу все поймете. Итак, я загадала двузначное число. Вы спрашиваете, например: «46?» Я отвечаю: «Все неверно». Вопрос: «52?» Ответ: «Одна цифра угадана, но она не на месте». Вопрос: «23?» Ответ: «Одна цифра угадана, но она не на месте». Вопрос: «35?» Ответ: «Верно».

Нужно прямо отметить, что вы играли очень хорошо. Каждый раз выбирали лучшие ходы, задавали наиболее правильные, наиболее полезные вопросы, старались «выжать» как можно больше знаний из сообщаемых мною сведений, пытались отсеять важное от второстепенного. Обычно люди играют хуже. Они не умеют извлечь суть из ответов и задают ненужные вопросы, которые не приближают, а, наоборот, отдаляют их от цели. Так, после первого ответа некоторые спрашивают: «64?», хотя уже ясно сказано: «Все неверно». Это означает, что нет смысла повторять ни одну из цифр, содержащихся в первом вопросе. Или после следующего ответа иногда спрашивают: «51?», считая, вероятно, что вторая часть ответа: «но она находится не на своем месте» – не содержит существенных сведений. Таким образом, в этом случае делается лишний ход.

На материале этой игры совершенно очевидно, насколько важно владеть умением разбираться в сведениях, имеющихся в условии задачи, анализировать получаемую информацию. Понятно и то, что, постоянно играя в подобные игры, это умение можно тренировать и развивать. Игровые ситуации станут сложнее, если увеличить число цифр в загадываемых числах.

Для упражнения в умении планировать ход решения задачи полезно использовать игры, непременное условие успешного решения которых – продумывать действия на несколько шагов вперед, и причем за себя и за противника. Попробуем сыграть в «Кто первый?». Ее смысл в том, что нужно по очереди увеличивать или уменьшать начальное число. И кто первый достигнет конечного, заранее установленного числа, тот и выиграл.

Игроки Петя и Вова договорились, что их цель – число 19, кто первый до него «доберется», тот и выиграл. Исходное число по обоюдному договору – 29. При этом условились, что можно вычитать либо 1, либо 2 за один ход. Начал Петя, сказав «28» (от 29 отнял 1) Вова: «26» (он в свой ход отнял 2). Петя: «24». Вова: «23». Петя: «21». Вова: «19» – и выиграл, потому что первый «добрался» до 19.

Понятно, что в такой игре могут участвовать и два, и три, и четыре человека. Допустимо увеличивать и уменьшать расстояние между исходным числом и конечным. Можно прибавлять или отнимать по отношению к начальному числу не только 1 или 2, но и 3, 4 и. т. п. Все зависит от того, как игроки договорятся между собой. В любом варианте этой игры, как вы догадываетесь, нужно уметь продумывать вперед возможные действия, как свои, так и партнера. На примере нашей игры хорошо видно, насколько важно уметь планировать их мысленно, в уме. Если человеку обязательно нужно план своих действий записывать на бумаге, то ему трудно рассчитывать на успех в таких играх.

Подводя итоги разговору о развитии трех наших умений, следует сказать, что полезно играть и в такие известные настольные игры, как шахматы, шашки, домино, нарды, «крестики-нолики» и т.п. Позиции партнеров в процессе подобных игр постоянно изменяются, все время необходимо тщательно анализировать складывающуюся обстановку, не забывая при этом планировать свои действия и предвидеть ходы противника. И конечно, нужно стремиться действовать, как хорошие игроки, которые после каждой партии (например, в шахматы) обдумывают, обсуждают ее особенности, выделяют удачные и безуспешные, ошибочные ходы, полезные и бесполезные действия.

Незаменимую пользу для развития мышления приносит также решение задач, построенных на материале этих игр: шашечных, шахматных и других. Неплохо иногда попрактиковаться и в сочинении таких задач, пусть даже очень простых, особенно если все – и решение, и сочинение – выполнять в мысленном плане, в уме, представляя то или иное расположение фигур и варианты возможных ходов.

В заключение нашего разговора хочется вновь напомнить, что каждый может стать сообразительным, если будет тренировать те три умения, о которых мы говорили, постоянно и неотступно, так, как обычно тренируют спортивные приемы или просто мышечную силу.

При решении любой задачи по любому школьному предмету старайтесь: 1) разобраться в ее содержании, выделить то, что дано, и то, что требуется, а также установить, что из данных более важно, а что – менее; 2) построить два плана решения задачи: один – сложный, состоящий из многих действий; второй – простой, включающий мало действий; при этом пытайтесь действовать мысленно; 3) после решения обдумывать способ действий, осмысливать его: придумывать разные задачи, для которых этот способ может пригодиться.

А теперь попробуйте применить полученные советы при решении такой задачи: «Через 7 лет Коле будет на 7 лет больше того, что было Сереже 7 лет назад. Кто старше и насколько?»