Преобразователи координат и фаз. Математическая основа преобразования координат поясняется на рис.61

Математическая основа преобразования координат поясняется на рис.61

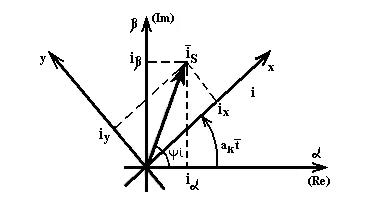
Рис.61 Преобразование координат

В неподвижной системе координат ( 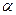, 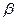) вектор тока (напряжения, потокосцепления) может быть представлен в алгебраической и показательной форме:

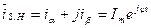
Аналогично, в системе вращающихся координат ( 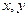), тот же вектор может быть представлен в виде:

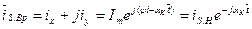
Отсюда легко получить уравнение перехода от неподвижной системы координат к вращающейся, и наоборот:

, ,

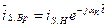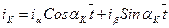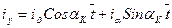
При построении реальных систем электропривода переменного тока, как асинхронных, так и синхронных, практически всегда в систему управления включаются преобразователи координат. Это обусловлено тем, что реальные токи в обмотках статора - это токи в неподвижной системе координат.

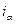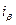Поэтому, как правило, современные электроприводы переменные тока содержат преобразователи обоих типов. Кроме того, они содержат преобразователи фаз 2/3 и 3/2. Первые преобразовывают токи и в фазные токи 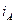, , 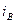, 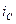в соответствии с выражениями:

, ,

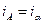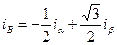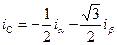
А вторые преобразовывают токи 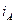, , 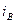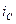в проекци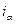и и 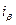, в соответствии с выражениями:

,

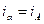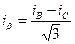
В итоге, функциональная схема электропривода приобретает вид, представленный на рис.62.

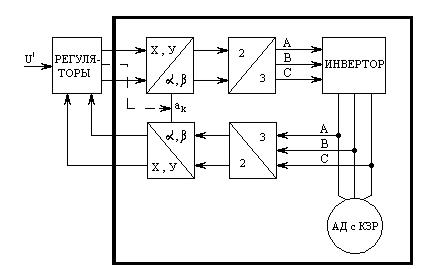
Рис.62 Функциональная схема асинхронного электропривода

В блоке регуляторов на основе задающего сигнала 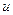и сигналов из каналов обратной связи, переменными состояниями вырабатываются сигналы управления во вращающейся системе координат, а также скорость вращения системы координат ( 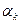). Затем эти сигналы переводятся в систему неподвижных координат, которые управляют инвертором. Используя вращающуюся систему координат при анализе и синтезе асинхронного электропривода, удается часть схемы, обведённую жирной линией на рис.62, описать одной системой уравнений (55) . это описание достаточно точно, когда инвертор управляется синусоидальным ШИМ. В этом случае моделирование не встречает больших затруднений.