Умножение на два разряда множителя одновременно.

Разбиение множителя на группы длиной k разрядов означает переход к новой системе счисления с основанием 2^k. Если при этом удается сократить количество элементарных действий, выполняемых при умножении (сложение и сдвиги), то сокращается время умножения. Остановимся более подробно на примере умножения на два разряда одновременно (k=2).

Возможны четыре случая сочетания разрядов множителя: 00, 01, 10, 11. Умножение на каждую из пар разрядов множителя должно выполняться за один такт автоматного времени, то есть в каждом такте умножения должно выполняться не более одного сложения. Рассмотрим умножение на эти пары на примере алгоритма А.

В случае пары 00 необходимо выполнить только сдвиг частичной суммы на два разряда - 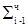2^-2 .

Для пары 01 выполняется добавление множимого в сумматор с последующим сдвигом суммы на два разряда - 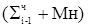2^-2 ,

При наличии пары 10 возможны следующие варианты действий:

a) 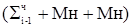2^-2 , то есть в этом случае происходят два сложения, что противоречит требованию;

б) 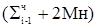2^-2, в этом случае требуется дополнительный регистр для хранения удвоенного Мн;

в) 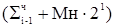2^-2, что соответствует добавлению к частичной сумме сдвинутого на один разряд влево множимого;

г) 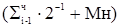2^-1, то есть частичная сумма сдвигается на один разряд вправо до и после добавления к ней множимого.

При умножении на пару 11 (к частичной сумме необходимо добавить утроенное множимое) ее можно представить в виде:

11 = (2² - 1)

М_Н ∙ 11= М_Н∙(2² - 1) = М_Н∙2²- М_Н, то есть в текущем такте к частичной сумме добавляется множимое, взятое со знаком минус. Добавление М_Н∙2² реализуется путем увеличения на единицу следующей старшей пары разрядов.

В приведенной ниже таблице представлены правила преобразования множителя для системы (0,1,1).

Таблица 1.

Анализируемая пара разрядов Мт	перенос из предыдущей пары	Преобразованная пара .
11
10

Пример: Мн = 0101

Мт = 11000111

Мт^п = 0101001001

Умножение будем осуществлять согласно алгоритму А.

[- Мн]_доп = 1.1011

2 Мн = 0.1010

0.0000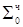

1.1011 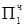= -Mн

1.1011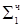

1.1110 11 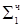∙ 2^-2

0.1010 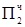= 2Mн

0.1000 11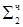

0.0010 0011 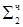∙ 2^-2

0.0000 100011 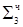∙ 2^-2 ( 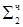∙ 2^-4)

1.1011 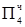=-Mн

1.1011 100011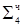

1.1110 11100011 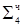∙ 2^-2

0.0101 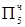= Mн

0.0011 11100011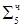

Время умножения на два разряда одновременно.

Появление любой из рассматриваемых пар множителей равновероятно. Следовательно, время умножения на два разряда множителя может быть выражено следующим соотношением: 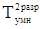= ( n/2 + 1) [0,75∙(t_сл + t_сдв) + (0,25∙t_сдв], где n – количество разрядов множителя.