Методика расчета двухкаскадной схемы умножителя частоты

Первый каскад (рис. 3.11) ,собранный на транзисторе VT1, работает в режиме отсечки. Для обеспечения угла отсечки близкого к оптимальному необходимо точку покоя сместить на входной характеристике транзистора левее начала координат на 0,2 В. Это смещение осуществляется за счет тока базы I_б0 = 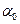I_mи.б, протекающего через резистор R_б1. При I_б0 = 30 мкА значение

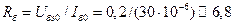кОм. (5.4)

Так как второй каскад умножения на транзисторе VT3 полностью аналогичен первому, то

R_б1 = R_б3 = 6,8 кОм.

Резисторы R_к1, и R_к3 входят в состав фильтра нижних частот, собранного на двух RC-звеньях. Кроме того, эти резисторы обеспечивают заданное напряжение U_кэ1 транзистораVT1 и U_кэ3 транзистора VT3. При расчете усилителей было установлено, что U_кэ = 4…5, В. Принимая во внимание U_кэ = 4,5 В, из уравнения

Е_к = R_к3 I_к30 + U_кэ3 (5.5)

находим

,

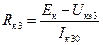где I_к30 = 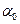I_mи.к3,

I_mи.к3 – амплитуда импульса коллекторного тока, протекающего через транзистор VT3,

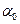– коэффициент Берга для постоянной составляющей тока коллектора.

При угле отсечки, например, 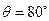коэффициент 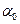= 0,27 (см. рис. 3.9).

Амплитуда импульса I_mи.к3 зависит от амплитуды входного сигнала и определяется с помощью входных и выходных характеристик транзистора, включенного по схеме с ОЭ (см. расчет усилителей п.п. 4.1, 4.2).

Сопротивление резистора R_к1 находится из уравнения

Е_к = R_к3 I_к10 + R_к1 I_к10 +U_кэ1.

Откуда получаем

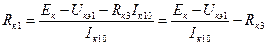, (5.6)

где I_к10 = 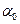I_mи.к1,

I_mи.к1 – амплитуда импульса коллекторного тока, протекающего через транзистор VT1, находится также графоаналитическим методом по входным и выходным характеристикам.

Емкости фильтра С_ф1 и С_ф2 находятся из условия

f_В1 = (m₁ + 0,5)f,

где f – частота входного сигнала (сигнала с выхода генератора),

m₁ – коэффициент умножения первого каскада.

Значение 0,5 прибавляется к m, чтобы АЧХ имела спад в интервале частот между двумя гармониками: m и (m+1), что позволяет подавить более высшие гармоники, рис. 5.4.

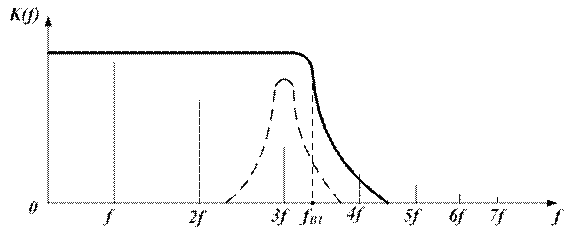
Рис. 5.4. К определению верхней частоты фильтра

Используя выражение (3.31)

,

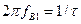где 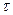= RC,

получаем выражение для расчета С_ф1:

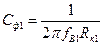. (5.8)

При расчете С_ф2 необходимо учесть, что входной сигнал имеет частоту m₁f. Тогда

f_В2 = (m₂ + 0,5)m₁f, (5.9)

где m₂ – коэффициент умножения второго каскада. Емкость конденсатора С_ф2 вычисляется по аналогичному (5.8) выражению

.

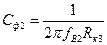При расчете усилителя с фиксированным напряжением на базе и эмиттерной стабилизацией, собранного на транзисторе VT2, следует учесть, что коллекторное напряжение для него понижено на величину R_к3I_к02, где I_к02 - значение коллекторного тока для точки покоя. Таким образом, методика расчета этого усилителя остается неизменной (см. п.п. 4.2), но вместо Е_к = 9В необходимо брать 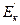=9В – R_к3I_к02.

При расчете колебательного контура необходимо учесть, что его АЧХ должна выделять нужную гармонику, как это показано на рис. 5.4 пунктирной кривой – АЧХ контура. Полоса пропускания контура должна быть

.

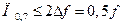Добротность контура Q и относительная полоса пропускания связаны следующим соотношением:

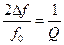, (5.10)

где 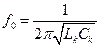– резонансная частота контура.

Принимая 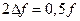, а f₀ = mf, получим следующую связь добротности контура с кратностью умножения частоты:

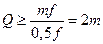. (5.11)

Для контура первого каскада умножения частоты (рис. 3.11) Q>2m₁, а для контура второго каскада Q>2m₁m₂.

Для нахождения значения L_k и C_k необходимо выполнение условия равенства энергий в магнитном поле катушки индуктивности и электрическом поле конденсатора:

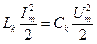. (5.12)

Из (5.12) находим, что отношение

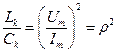, (5.13)

где 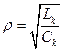– волновое сопротивление контура.

Если известны потери мощности колебаний в контуре, то можно ввести сопротивление потерь r. Это сопротивление учитывает преобразование энергии электромагнитных колебаний в тепло и другие виды энергии. Тогда

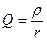. (5.14)

С учетом выражения (5.11) имеем

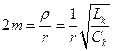. (5.15)

Значение r можно определить, исследуя свободные колебания в контуре. Они затухают по закону

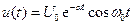, (5.16)

где 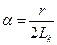. (5.17)

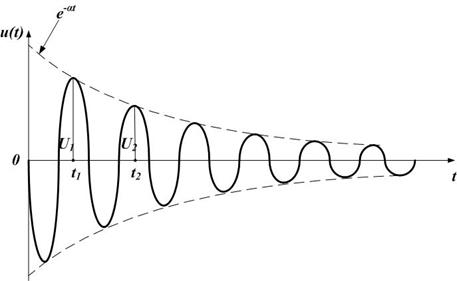
Рис. 5.5. Затухание колебания в контуре (напряжение на конденсаторе)

Отношение двух соседних амплитуд (рис. 5.5)

,

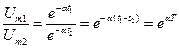где Т – период собственных колебаний.

При высокой добротности соседние амплитуды мало различаются, поэтому целесообразно брать отношение

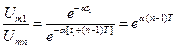. (5.18)

Из (5.18) логарифмированием находим

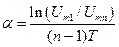. (5.19)

Подставляя (5.19) в (5.17), получаем связь

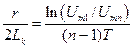. (5.20)

Итак, для расчета L_k и C_k контура следует использовать выражения:

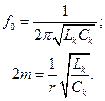(5.21)

где r определить экспериментально, используя выражение (5.20).