Погрешность выполнения арифметических операций

Выбор длины разрядной сетки и формы представления чисел тесно связаны с точностью получаемых при арифметических операциях результатов. При выполнении операций над числами с фиксированной запятой можно считать что результат точен (при условии отсутствии переполнения).

При выполнении операций над числами, представленными в форме с плавающей запятой, требуется выравнивание порядков. Это может приводить к потере некоторых разрядов мантиссы.

Рассмотрим арифметические операции над операндами, заданными с абсолютными погрешностями: А=[A]+∆A и B=[B]+∆B.

A+B=[A]+[B]+(∆A+∆B),

где абсолютная погрешность суммы ∆(A+B)=∆A+∆B.

A-B=[A]-[B]+(∆A-∆B),

где абсолютная погрешность разности ∆(A-B)=∆A-∆B.

A×B=[A][B]+[A]∆B+[B]∆A+∆A∆B

произведением ∆A∆B можно пренебречь, следовательно,

A×B≈[A][B]+[A]∆B+[B]∆A,

то есть абсолютная погрешность произведения ∆(AB)≈[A]∆B+[B]∆A.

При выполнении операции деления

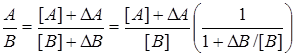
абсолютная погрешность частного ∆(A/B)=∆A/[B]-[A]∆B/([B])².