Округление

Речь идет об округлении только дробных чисел, целые не округляются. Так как в ЭВМ используются числа с конечным числом разрядов, а также часто выполняются операции приведения данных одной размерности к данным другой, то операция округления выполняется достаточно часто.

В общем виде число с плавающей запятой размещенное в разрядной сетке размерностью k имеет вид A_r=m_ar^k . Если для записи мантиссы используются только n разрядов, то число может быть представлено в виде двух частей: A_r=[m_a]rⁿ+[A₀]r^k-n, где [A₀]r^k-n=A₀ – часть числа не вошедшая в разрядную сетку размерностью k.

В зависимости от того, как учитывается А₀, при записи числа А в n-разрядную сетку, можно выделить несколько способов округления чисел.

1. Отбрасывание А₀. При этом возникает относительная погрешность

õ_окр=|А₀|r^k-n/(|m_A|rⁿ), так как r ^-1≤ |m_A| <1, 0≤ |A₀| <1, то õ_окр=r^--(n-1).

2. Симметричное округление. При этом производится анализ величины А₀:

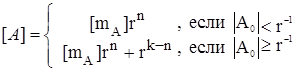
При условии |А₀|≥r^-1 единица добавляется к младшему разряду мантиссы. Данный способ округления наиболее часто используется на практике.

3. Округление по дополнению. В этом случае для округления используется (n+1)-й разряд. Если в нем находится единица, то она передается в n-й разряд, иначе разряды начиная с (n+1)-го отбрасываются.

4. Случайное округление. Генератор случайных чисел формирует нулевое или единичное значение, посылаемое в младший разряд мантиссы.

Оценка точности вычислений зависит как от вида выполняемых операций, так и от последовательности их следования друг за другом.