Распределение энергии по степеням свободы.
Средняя энергия, приходящаяся на одну молекулу `E 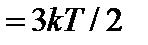 . Если считать молекулу шариком (как в одноатомном газе), то средняя энергия такой частицы определяется средней кинетической энергией ее поступательного движения. Энергию эту можно представить как сумму трех слагаемых – кинетических энергий движения молекулы по трем взаимно перпендикулярным направлениям:
. Если считать молекулу шариком (как в одноатомном газе), то средняя энергия такой частицы определяется средней кинетической энергией ее поступательного движения. Энергию эту можно представить как сумму трех слагаемых – кинетических энергий движения молекулы по трем взаимно перпендикулярным направлениям: 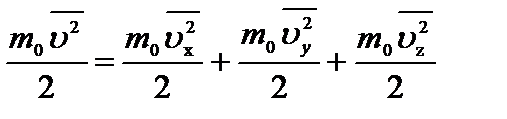 ,
,
где ux, uy, uz – составляющие скорости молекул по трем осям координат. Из-за хаотичности молекулярного движения можно считать, что средние значения кинетических энергий по трем направлениям равны друг другу: 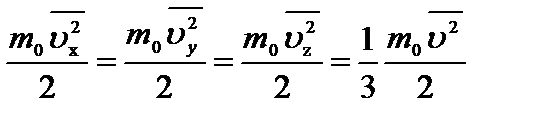 (1)
(1)
Так как 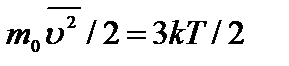 , то каждое из трех слагаемых равенства (1) равно kT/2.
, то каждое из трех слагаемых равенства (1) равно kT/2.
Разделение кинетической энергии частицы на три независимые составляющие связано с тем, что частица рассматривается как свободная материальная точка, обладающая тремя степенями свободы.
Число степеней свободы – наименьшее число линейно независимых координат, которые полностью определяют положение тела в пространстве. Значит, на каждую степень свободы одноатомной молекулы приходится энергия, равная kT/2. Естественно было предположить, что если бы молекула газа обладала еще какими-нибудь степенями свободы, то и на каждую из них пришлась бы кинетическая энергия kT/2.
Действительно, в классической статистической физике такая теорема доказывается (Больцман): в совокупности большого числа молекул, находящихся в тепловом равновесии при температуре Т, средняя кинетическая энергия равномерно распределена между всеми степенями свободы и для каждой степени свободы молекулы она равна kT/2.
Эта теорема называется законом равномерного распределения кинетической энергии по степеням свободы, или, законом равнораспределения.
Двух- и многоатомные газы отличаются от одноатомных числом степеней свободы. Двухатомную молекулу можно представить себе в виде системы, состоящей из двух атомов, жестко закрепленных на некотором расстоянии. Здесь три степени свободы приходятся на поступательное движение центра масс, и две – на вращательное. Вращение молекулы вокруг оси 0х не вносит изменения в кинетическую энергию. Следовательно, число степеней свободы жесткой двухатомной молекулы равно 5. Трехатомный газ имеет 6 степеней свободы. Таким образом, если молекула обладает i степенями свободы, то средняя кинетическая энергия теплового движения этой молекулы: 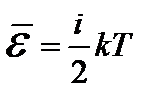 .
.
Дата добавления: 2015-04-01; просмотров: 2043;
