Велосипедный спорт
Велосипедист должен преодолеть три силы сопротивления (рис. 15.36):
— силу сопротивления встречного потока воздуха;
Рис. 15.36.
Посадка велогонщика

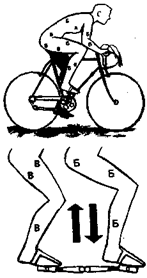
Рис. 15.37.Мышцы, участвующие в процессе езды велосипедиста:
А — дыхательная мускулатура, Б — мышцы, участвующие в перемещении педали вниз,В — мышцы, участвующие в перемещении педали вверх
— силу трения качения (см. рис. 6.5, табл. 6.2);
— сталкивающую силу при подъеме на гору.
Внешним силам сопротивления спортсмен противопоставляет силу своих мышц, правильную посадку и пр.
На рис. 15.37, показаны мышцы, работающие в процессе нажимания на педали.
Главное препятствие для преодоления дистанции — встречный поток воздуха. Чем выше скорость, тем больше сила сопротивления встречного потока воздуха. Сопротивление воздуха можно уменьшить несколькими способами.
Сила сопротивления воздушного потока fb зависит от следующих факторов:
А — величина поверхности сопротивления, которую можно изменить посадкой;
Кc — коэффициент сопротивления, который зависит от обтекаемости фигуры велосипедиста и от величины поверхности одежды;
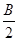 — плотность воздуха, которая на равнине примерно постоянна, а в горных районах несколько ниже;
— плотность воздуха, которая на равнине примерно постоянна, а в горных районах несколько ниже;
V2 — квадрат скорости. Сопротивление воздуха растет, следовательно, не пропорционально скорости велосипедиста, а гораздо сильнее. 
При встречном ветре эта сила увеличивается, при попутном — уменьшается, что дает уменьшение или увеличение скорости. Для уменьшения силы сопротивления встречного потока воздуха необходимо сесть так, чтобы поверхность (А), которую вы занимаете, была относительно небольшой. В спринте — предпочтительно совершать (принимать) горизонтальную посадку. Для уменьшения сопротивления воздуха используют (применяют) специальные шлемы и обтекаемые костюмы (комбинезоны).
На скорость перемещения велосипедиста влияет сила трения качения (трение шин о покрытие шоссе). Чем тяжелее велосипедист, тем больше трение качения, а также чем толще шины и меньше они накачаны — тем больше трение качения. Влияют на скорость велосипедиста также качество покрытия шоссе, размер колес.
Сила трения качения Fmр зависит от следующих факторов:
— Fн — нормальная сила соответствует весу спортсмена с велосипедом, если он направлен перпендикулярно к поверхности, по которой происходит перемещение;
— r — радиус колес;
— f — расстояние между теоретической точкой опоры шины и фактической точкой встречи шины с поверхностью, по которой происходит перемещение. Отсюда имеем формулу:
Посадка велосипедиста во  время шоссейной гонки должна быть максимально обтекаемой и в то же время не мешать работе внутренних органов (рис. 15.38). Посадка велосипедиста на подъеме может быть такой: 1) кисти рук на тормозных рычагах; 2) кисти в центре руля, обхватывают его снизу; 3) положение, при котором переносится центр тяжести тела.
время шоссейной гонки должна быть максимально обтекаемой и в то же время не мешать работе внутренних органов (рис. 15.38). Посадка велосипедиста на подъеме может быть такой: 1) кисти рук на тормозных рычагах; 2) кисти в центре руля, обхватывают его снизу; 3) положение, при котором переносится центр тяжести тела.
Во время подъема скорость небольшая, решающую роль приобретает сталкивающая сила, а сопротивлением встречного воздушного потока можно пренебречь.

Рис. 15.38. Посадка велосипедиста при шоссейных гонках
Для сталкивающей силы (F.) решающими являются следующие факторы:
G — суммарный вес спортсмена с велосипедом;
l — длина пути;
h — высота подъема на 100 м пути

Чем больше вес спортсмена с велосипедом и крутизна подъема (например, при перепаде высот 6 м на 100 м подъема — 6%), тем больше сталкивающая сила.
При выполнении поворота возникает центробежная сила, величина которой зависит от трех факторов: 1) чем больше скорость и вес спортсмена с машиной и чем меньше радиус закругления, тем больше центробежная сила; 2) для противодействия центробежной силе следует наклониться вместе с велосипедом в сторону закругления. На рис. 15.39 показаны центробежная сила и направление взаимодействия других сил, возникающих при прохождении виража; 3) в зависимости от формы виража и скорости необходимо наклониться так, чтобы угол между велосипедом и поверхностью трека составлял от 70° до 110°. В идеальном варианте он должен быть равен 90°.
Но в некоторых ситуациях гонщик должен ехать по треку медленно, например, в спринте, парной групповой гонке и т. д. В этих случаях при слишком маленькой скорости можно упасть, так как колесо соскользнет вниз. При медленной езде или попытке полностью остановиться центробежные силы незначительны или даже равны нулю, а значит наклоняться на вираже нельзя.
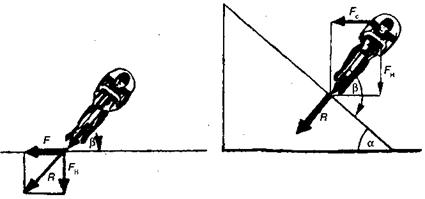
Рис. 15.39.Силы, действующие на велосипедиста при прохождении виража:F— центробежная сила, FH — нормальная сила, R — результирующая, α — угол крутизны трека, Fc — сталкивающая сила, β — угол наклона
Преимущество езды сверху заключается в возможности использовать сталкивающую силу (Fc) для значительного увеличения скорости. Сталкивающая сила прямо пропорциональна высоте кривой (h) и весу велосипедиста с машиной (G).

Чем тяжелее спортсмен и чем выше располагается он на вираже, тем больше сталкивающая сила. Преимущество будет на стороне гонщика, если при выходе из финишного виража он окажется в верхней его части на одном уровне с соперником.
Прыжки
При прыжках обе ноги после сгибания в главных своих суставах (тазобедренных, коленных, голеностопных) выпрямляются быстрым и сильным сокращением разгибателей и отрываются от земли толчком, который передается телу. При этом прыжок или совершается на месте — тело поднимается в вертикальном направлении, или же телу сообщается поступательное движение вперед и вверх (рис. 15.40).
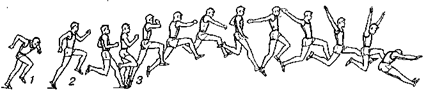
Рис. 15.40. Прыжки в длину с разбега
Прыжки в длину с разбега. Чем быстрее человек бежит, тем дальше он может прыгнуть. Кинетическая энергия бега может также при известных обстоятельствах использоваться для прыжков в высоту. На этом принципе основаны прыжки с шестом (G.H. Dyson, 1962).
Перед прыжком центр тяжести уже находится на высоте около 90 см над землей, а во время прыжка оказывается лишь немного выше планки. Например, при использовании метода «вестерн-ролл» центр тяжести (ЦТ) тела может подниматься над планкой на высоту около 15 см (G.H. Dyson, 1962).
Когда человек прыгает «с места», каждая из участвующих в этом акте мышц сокращается только один раз. Максимальная сила, развиваемая мышцей, пропорциональна площади ее поперечного сечения. Возможное укорочение мышцы пропорционально ее длине. Следовательно, работа, которую она может совершить при одиночном сокращении, пропорциональна произведению ее длины на площадь поперечного сечения, т. е. ее объему. Мышцы одинакового объема (или веса) способны совершать одинаковую работу. Представим теперь животное, масса которого т, а мышцы, участвующие в прыжке, — масса т'. Пусть эти мышцы при одиночном сокращении способны совершать работу Km'. Эта работа равна кинетической энергии, которую приобретает тело животного при отрыве от земли:

где и — скорость в момент отрыва. Если бы животное прыгнуло вертикально, оно поднялось бы на высоту 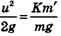 . В случае прыжка под углом 45° оно опустилось бы на расстоянии
. В случае прыжка под углом 45° оно опустилось бы на расстоянии 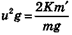 от начального пункта. Поэтому можно ожидать, что разные животные, у которых отношения массы используемых при прыжке мышц к общей массе тела равны (т. е. равны величины
от начального пункта. Поэтому можно ожидать, что разные животные, у которых отношения массы используемых при прыжке мышц к общей массе тела равны (т. е. равны величины 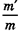 ), способны прыгать на одинаковую высоту и одинаковое расстояние независимо от размеров тела.
), способны прыгать на одинаковую высоту и одинаковое расстояние независимо от размеров тела.
Попробуем теперь исходить из иного предположения относительно мышц. Будем считать, что способность совершать прыжки ограничивается максимальной мощностью, которую могут развить мышцы, и что единица массы мышечной ткани может развивать мощность KI. Пусть за время от начала сокращения мышц до момента отрыва ног от земли центр тяжести (ЦТ) животного перемещается на расстояние l. Для большинства животных l будет немного меньше длины ног. Мы уже знаем, что к моменту отрыва от земли должна быть совершена работа 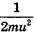 . Чтобы найти необходимую мощность, нам нужно разделить эту работу на время t, за которое она производится. Проходя путь / за время t, животное увеличивает свою скорость от 0 до U. Предположим, что ускорение постоянно и используем уравнение. Тогда получим
. Чтобы найти необходимую мощность, нам нужно разделить эту работу на время t, за которое она производится. Проходя путь / за время t, животное увеличивает свою скорость от 0 до U. Предположим, что ускорение постоянно и используем уравнение. Тогда получим
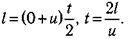 (15.8)
(15.8)
Мощность, необходимая для совершения работы 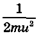 за это время, составляет
за это время, составляет 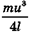 , а мощность, которую могут развивать используемые при прыжке мышцы, равна Km1. Отсюда
, а мощность, которую могут развивать используемые при прыжке мышцы, равна Km1. Отсюда
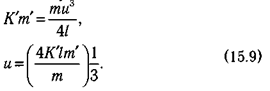
Если животное отрывается с этой скоростью от земли вертикально вверх, оно достигает высоты. 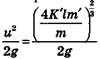 Если же оно отрывается под углом 45°, оно прыгнет на расстояние
Если же оно отрывается под углом 45°, оно прыгнет на расстояние 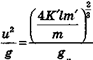 .
.
Для животных разной величины, но с одинаковой относительной массой мышц, используемых при прыжке, наибольшая высота и длина прыжков должна быть пропорциональна пути ускорения (т. е. пути, на котором скорость равномерно возрастает от 0 до и) в степени 2/3. Спортсмен может прыгнуть в длину с разбега на расстояние до 8 м. С помощью рассмотренных выше формул мы можем приблизительно определить начальную скорость, с которой спортсмен должен оторваться от земли (скорость отрыва). В случае оптимального угла отрыва от земли в 45° необходимая скорость определяется
из уравнения 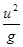 = 800, отсюда
= 800, отсюда
и = 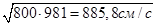 (15.10)
(15.10)
Следовательно, скорость отрыва от земли составляет 885,8 см/с без учета сопротивления воздуха.
Если угол отрыва равен 55°, а дальность прыжка та же, то спортсмен должен отрываться от земли со скоростью, которую можно найти из уравнения
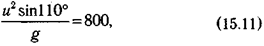
значит,
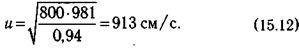
Если бы при этом ускорение было постоянным, его можно было бы вычислить по формуле:
(913)2=2a·4, (15.13)
а = 104196 см/сек2.
Если масса тела спортсмена равна m граммов, то для того, чтобы придать ему такое ускорение, понадобилась бы сила 104 196 m дин. Одна дина — это сила, необходимая для того, чтобы сообщить массе в 1 г ускорение, равное 1 см/с2 (т. е. увеличить ее скорость на 1 см/с за каждую секунду).
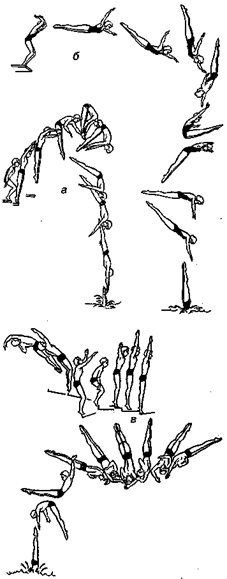
Рис. 15.41. Прыжки в воду.
а — из передней стойки полуоборот вперед согнувшись; - из передней стойки полтора оборота вперед «летом» согнувшись; в — полтора оборота назад с двумя с половиной винтами
Дата добавления: 2015-05-03; просмотров: 1179;
