Вязкость воды при различных температурах
| t, °С | ||||||||||
| η•106 кг/м·с | ||||||||||
| t,°C | ||||||||||
| η ·106 кг/м·с |
Таблица 15.5
Кинематическая вязкость некоторых жидкостей при 20° (HadgmanC.D., 1965)
| Среда | Вязкость, ПЗ | Плотность, г/см3 | Кинематическая ВЯЗКОСТЬ, СМ2/С |
| Воздух | 1,8•10 -4 | 1,3 • Ю-3 | 0,14 |
| Вода | 0,010 | 1,00 | 0,010 |
Вода препятствует продвижению пловца. В гидродинамике для расчета движения жидкости используют число Рейнольдса. Число Рейнольдса — это безразмерная величина 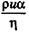 , где
, где 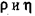 — плотность и вязкость жидкости, и — скорость ее движения относительно тела и а — некоторая длина.
— плотность и вязкость жидкости, и — скорость ее движения относительно тела и а — некоторая длина.
Правило, согласно которому строение потока около тел одной и той же формы одинаково, если одинаково число Рейнольдса, неприменимо в тех случаях, когда речь идет о поведении жидкости около ее свободной поверхности.
Число Рейнольдса удобно выражать как 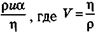 величина, называемая кинематической вязкостью.
величина, называемая кинематической вязкостью.
Во многих случаях трудно измерять силы, которые действуют на тело, движущееся в жидкости. В этой связи для экспериментов используют аэродинамические и гидродинамические трубы.
Лобовое сопротивление. При движении какого-нибудь тела в жидкости, на него действует сила, задерживающая его движение. Эту силу называют лобовым сопротивлением. Величина ее зависит от природы жидкости и от размеров, формы и скорости движущегося тела.
Как показали эксперименты в аэродинамических трубах, лобовое сопротивление тела или различных тел одной и той же формы можно определить по формуле 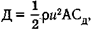 где Д — лобовое сопротивление, р — плотность жидкости, и — скорость движения жидкости относительно тела, А — характеристическая площадь и Сд — величина, называемая коэффициентом лобового сопротивления, которая зависит от формы тела и от числа Рейнольдса.
где Д — лобовое сопротивление, р — плотность жидкости, и — скорость движения жидкости относительно тела, А — характеристическая площадь и Сд — величина, называемая коэффициентом лобового сопротивления, которая зависит от формы тела и от числа Рейнольдса.
К сожалению, не существует единого определения А, которое было бы удобным при любой форме тела. Используются следующие площади:
1) лобовая площадь, т. е. площадь проекции тела на плоскость, перпендикулярно направлению потока. В случае цилиндра, имеющего высоту h и радиус г, лобовая площадь будет равна πr2, если ось цилиндра параллельна потоку, и 2rh, если она перпендикулярна ему;
2) площадь наибольшей проекции, т. е. проекции по тому направлению, по которому площадь ее будет наибольшей; эту величину используют, когда имеют дело с обтеканием профиля крыла; по сравнению с лобовой площадью она имеет то преимущество, что не изменяется при наклоне профиля;
3) суммарная поверхность тела. Следует помнить, что в случае тонкой пластинки это будет суммарная площадь обеих ее сторон.
Если есть сомнения, то важно указать, какая именно из этих площадей была использована при вычислении коэффициента С
На рис. 15.34 приведены кривые зависимости коэффициента лобового сопротивления Сд от числа Рейнольдса для тел различной формы.
Все коэффициенты были вычислены на основе лобовой площади.
Число Рейнольдса для всех тел, кроме диска, определялось обычным способом по длине, измеренной в направлении потока; для диска же его определяли по диаметру, хотя он расположен перпендикулярно потоку.
В связи с отсутствием работы по лобовому сопротивлению у пловцов, мы приводим данные Т.О. Lang, K.S. Norris (1966), R. Alexander (1968) полученные при изучении дельфинов. Было найдено, что при коротких «бросках» дельфин может развивать скорость до 830 см/с (около 16 узлов), а со скоростью 610 см/с (около 12 узлов) способен плыть примерно в течение 1 мин. Дельфин (Turbiopsgilli) имел длину 191 см, так что число Рейнольдса при первой из этих скоростей составляло 830·191 /0,01 = 1,6·107. Профиль дельфина хорошо обтекаем. Кожа очень гладкая и лишена волос. Все указывает на малую величину лобового сопротивления.
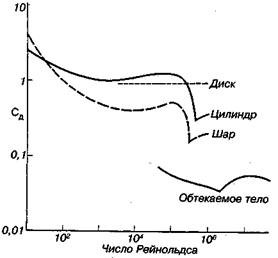
Рис. 15.34.Зависимость коэффициента лобового сопротивления от числа Рейнольдса для диска, расположенного перпендикулярно направлению своего движения; для удлиненного цилиндра, движущегося перпендикулярно своей оси; для шара и для тела обтекаемой формы, движущегося вдоль своей оси (по Р. Александер, 1970)
Попробуем оценить величину лобового сопротивления для дельфина, плывущего со скоростью 830 см/с и мощность, развиваемую его мышцами. Лобовая площадь у дельфина длиной 191 см, вероятно, составляет около 1100 см2. Коэффициенты лобового сопротивления для обтекаемых тел при числе Рейнольдса около 1,6-107 близки к 0,055. Подставив эти величины в уравнение
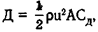 мы найдем, что лобовое сопротивление у нашего дельфина составляет примерно 1 /2 (830)2·1100·0,055 = 2,0-107 дин. Мощность равна сопротивлению, умноженному на скорость, т. е. в данном случае 830·2,0·107 эрг/с, или 1660 Вт. Однако от мышц требуется большая мощность, так как КПД дельфина при плавании не может достигать 100%; поэтому она едва ли могла быть меньше 2000 Вт. Дельфин весит 89 кг, из которых на долю участвующих в плавании мышц приходится, вероятно, около 15 кг. Таким образом, мощность мышц должна составлять примерно 130 Вт/кг. Это в 3 раза больше максимальной мощности, которую могут развивать мышцы человека при работе на велоэргометре.
мы найдем, что лобовое сопротивление у нашего дельфина составляет примерно 1 /2 (830)2·1100·0,055 = 2,0-107 дин. Мощность равна сопротивлению, умноженному на скорость, т. е. в данном случае 830·2,0·107 эрг/с, или 1660 Вт. Однако от мышц требуется большая мощность, так как КПД дельфина при плавании не может достигать 100%; поэтому она едва ли могла быть меньше 2000 Вт. Дельфин весит 89 кг, из которых на долю участвующих в плавании мышц приходится, вероятно, около 15 кг. Таким образом, мощность мышц должна составлять примерно 130 Вт/кг. Это в 3 раза больше максимальной мощности, которую могут развивать мышцы человека при работе на велоэргометре.
Лобовое сопротивление — не единственная гидродинамическая сила, действующая на тела, которые движутся в жидкости или находятся в потоке. По определению оно имеет то же направление, что и скорость движения жидкости относительно тела. Когда симметричное тело движется вдоль своей оси симметрии, действующая на него гидродинамическая сила направлена прямо и представляет собой лобовое сопротивление. Но когда симметричное тело движется под некоторым углом к оси симметрии, гидродинамическая сила действует под углом к его пути. Ее можно разложить на две составляющие, одна из которых направлена назад и представляет собой лобовое сопротивление, а другая действует под прямым углом к первой.
Энергетика пловца. Когда человек плывет, он сообщает некоторое количество энергии воде, чтобы продвинуться (проплыть) в ней. Это создает волну, которая в конечном счете потеряет всю сообщенную ей энергию в виде тепла, и поверхность воды снова станет спокойной. Затраченная таким образом при плавании энергия представляет собой совершенную работу плюс тепло, потерянное телом пловца.
Дата добавления: 2015-05-03; просмотров: 1791;
