Коэффициент давления

Поместим в газовой поток дозвуковой скорости некоторый криволинейный профиль и рассмотрим изменение параметров элементарной струйки, охватывающей такой профиль (рис. 10.1).

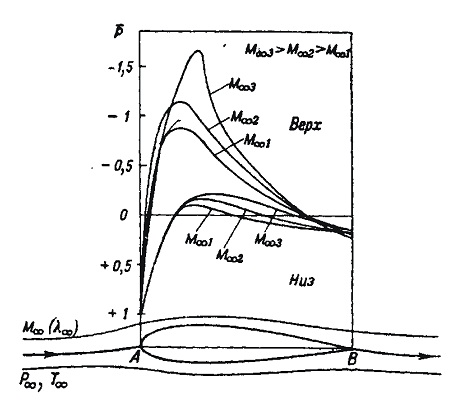
Рисунок 10.1 - Распределение коэффициентов давления по профилю

Создаваемые профилем возмущения потока при дозвуковых скоростях будут распространяться во всех направлениях, в том числе и против течения. Под влиянием этих возмущений элементарные струйки, движущиеся к профилю, будут деформироваться. У носика профиля центральная струйка расширяется; скорость течения при этом падает и в точке разветвления А обращается в нуль. В этой точке параметры будут равны параметрам полного торможения потока. На передней части профиля сечение струйки уменьшается, вследствие чего скорость увеличивается, а давление падает. На верхней и нижней поверхностях профиля продолжается поджатие струйки с соответствующим нарастанием скорости. В некоторой точке сечение струйки минимально. В этом месте скорость будет максимальной. Далее, на задних поверхностях профиля струйка вновь расширяется, скорость ее падает, а давление растет.

Таким образом, в результате деформации струек, характер которой определяется формой обтекаемого тела, вдоль поверхности профиля давление меняется. Распределение давлений обусловливает возникновение аэродинамических сил, действующих на профиль: подъемной силы, вызванной разностью давлений на верхней и нижней поверхностях профиля, и силы лобового сопротивления, вызванной разностью давлений на переднюю и заднюю части профиля и силами трения.

Распределение давлений вдоль обтекаемой поверхности характеризуется безразмерной величиной - коэффициентом давления, который определяется как отношение разности давлений в данной точке на поверхности и статического в бесконечности к скоростному напору невозмущенного потока:

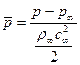. (10.9)

Коэффициент давления можно определить и по следующей формуле:

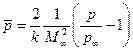, (10.10)

где 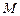- число Маха:

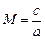, (10.11)

где 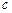- скорость потока;

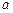- местная скорость звука.

Пояснение:

,

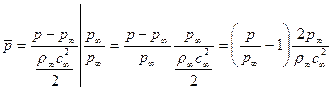так как 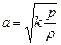(9.17), то получим: и используя (10.11), получим:

.

Число Маха является критерием подобия в механике жидкости и газа и представляет собой отношение скорости течения в данной точке газового потока к местной скорости распространения звука в движущейся среде. Назван по имени австрийского ученого Эрнста Маха.

Если в рассматриваемой области скорости меньше критической, т. е. если:

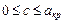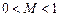, то . (10.12)

Если скорости течения больше критической:

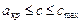, то 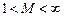, (10.13)

где 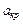- критическая скорость, то есть скорость течения 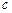равная местной скорости звука 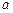[см. прим.];

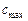- максимальной скорость течения. (Если применить уравнение энергии к двум сечениям трубки тока, в одном из которых давление 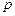уменьшается до нуля, то скорость течения 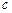будет стремиться к некоторой максимальной величине 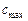, которая удовлетворяет истечению газа в пустоту ( 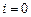; ; 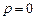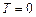). При максимальной скорости течения 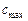вся тепловая энергия молекул преобразуется в энергию направленного движения. Практически максимальная скорость течения недостижима и является известным теоретическим пределом для скорости газа. Следует иметь в виду, что с приближением скорости течения к максимальной разрежение газа становится весьма большим и поэтому к рассматриваемому потоку нельзя применять уравнение энергии в известной нам форме (9.7)).

В первом случае (10.12) течение называется дозвуковым или докритическим; а во втором (10.13) - сверхзвуковым или сверхкритическим. Следовательно, значение безразмерной скорости 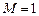разделяет области течений с дозвуковыми (докритическими) скоростями и со сверхзвуковыми (сверхкритическими) скоростями.

При малых скоростях набегающего потока более удобно для подсчета коэффициента давления пользоваться формулой (10.9).

10.3 Критическое число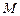

На рис. 10.1 показано примерное распределение 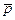вдоль поверхности профиля. До тех пор, пока скорость значительно меньше скорости звука, характер деформации струек, а вместе с тем и картина распределения коэффициентов давления по профилю при изменении скорости невозмущенного потока сохраняются практически неизменными. Однако по мере увеличения влияние сжимаемости сказывается все более ощутимо; распределение 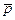по профилю начинает меняться особенно сильно там, где местные скорости в струйке (на поверхности профиля) велики. В минимальном сечении струйки скорость наибольшая. Найдем зависимость между безразмерной скоростью 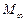и скоростью в некоторой точке на профиле .

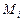С этой целью воспользуемся формулой (10.10), заменив в ней отношение давлений через соответствующие числа М, с учетом, что:

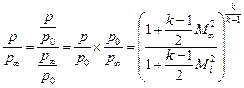и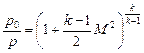

получим

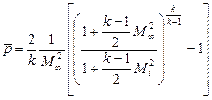, (10.14)

где 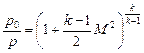- формула отношения давлений в предположении изоэнтропического течения, являющаяся модификацией уравнения энергии, полученного путем преобразования уравнения (9.7) и введения безразмерной скорости .

При некотором значении , которое обозначим через 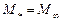в минимальном сечении трубки тока устанавливается критическая скорость 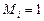. Соответствующая величина коэффициента давления будет равна:

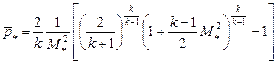, (10.15)

Величина 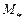, называется критическим числом 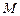набегающего потока. Оно определяет то значение безразмерной скорости набегающего потока, при котором максимальная местная скорость на контуре тела становится равной местной скорости звука.

Из определения критического числа 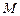(см. выше), следует, что эта величина 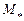разграничивает дозвуковые режимы обтекания тела на две группы. Первая группа докритических режимов ( 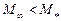) характеризуется тем, что во всех точках поля потока местные скорости дозвуковые ( 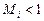). Ко второй группе ( 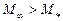) относятся режимы обтекания с местными сверхзвуковыми скоростями.

Примечание: [При дозвуковом обтекании фюзеляжа, крыла и оперения самолёта на выпуклых участках их обводов возникают зоны местного ускорения потока. Когда скорость полёта летательного аппарата приближается к звуковой, местная скорость движения воздуха в зонах ускорения потока может несколько превысить скорость звука (рис. 10.2). Миновав зону ускорения, поток замедляется, с неизбежным образованием ударной волны (таково свойство сверхзвуковых течений: переход от сверхзвуковой скорости к дозвуковой всегда происходит разрывно - с образованием ударной волны). Интенсивность этих ударных волн невелика - перепад давления на их фронтах мал, но они возникают сразу во множестве, в разных точках поверхности аппарата, и в совокупности они резко меняют характер его обтекания, с ухудшением его лётных характеристик: подъёмная сила крыла падает, воздушные рули и элероны теряют эффективность, аппарат становится неуправляемым, и всё это носит крайне нестабильный характер, возникает сильная вибрация. Это явление получило название волнового кризиса. Когда скорость движения аппарата становится сверхзвуковой (М > 1), течение вновь становится стабильным, хотя его характер изменяется принципиально (рис. 10.3).]

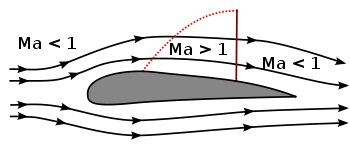
Рисунок 10.2 - Аэрокрыло в близком к звуковому потоке

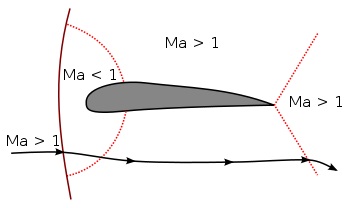
Рисунок 10.3 - Аэрокрыло в сверхзвуковом потоке