Средства создания векторных изображений

Векторные изображения создаются в векторной графике математическими формулами, а не координатами точек, как в растровой графике. Основу изображений в векторной графике создают векторы или контуры. Каждый из контуров можно создавать, редактировать и удалять независимо от других. Поэтому векторную графику называют объектно-ориентированной графикой.

Отсюда формулируется задача - поиск формулы, которая бы позволяла описывать все многообразие линейных контуров. И поскольку дискретизация имеет линейный характер, общий контур разбивается на достаточно мелкие фрагменты - сплайны. При этом необходимо выбрать наиболее простую формулу (функцию) для их описания, представляемую в параметрической форме. Одной из самых важных причин выбора в качестве средств векторной графики кривых Безье и NURBS-кривых является управляемая гладкость, а также то, что их форма определяется расположением множества контрольных точек, которые определяют форму только части кривой, находящейся рядом.

В программах векторной графики единственный способ изменения формы - интерактивное перемещение опорных и управляющих точек.

На базе кривой Безье основывается и язык описания страниц PostScript, развитие которого шло по пути интегрирования новых возможностей выводных устройств (цветной печати, систем управления цветом и шрифта).

В качестве формулы, которая была бы достаточно простой (с точки зрения математика), универсальной (с точки зрения программиста) и геометрически наглядной (с точки зрения пользователя - художника или дизайнера), чаще всего используется упомянутая кривая Безье. Кривые Безье - параметрические кривые третьего порядка.

На самом деле, это целое семейство кривых, из которых используется частный случай с кубической степенью, т. е. кривая третьего порядка, описываемая следующим параметрическим уравнением

R(t) = P_o(l-t)³ + P₁t(l-t)² + P₂t²(l-t) + Р₃t³, где 0 < t < 1

Общий вид элементарной кривой Безье представлен на рисунке 32. Такую кривую можно построить, если известны координаты четырех точек, называемых контрольными.

Из четырех контрольных точек кривая проходит только через две, поэтому эти точки называются опорными —anchor points (иначе они называются узлами(nodes), поскольку "связывают" элементарные кривые друг с другом, чтобы образовать сложный единый контур).

Две другие контрольные точки не лежат на кривой, но их расположение определяет кривизну кривой, поэтому эти точки иначе называются управляющими точками, а линии, соединяющие управляющую и опорную точки, управляющей линией (в просторечии именуемых "рычагами").

Кривая Безье является гладкой кривой, т. е. она не имеет разрывов и непрерывно заполняет отрезок между начальной и конечной точками.

Кривая начинается в первой опорной точке, касаясь, отрезка своей управляющей линии, и заканчивается в последней опорной точке, также касаясь, отрезка своей управляющей линии. Это позволяет гладко соединять две кривые Безье друг с другом: управляющие линии располагаются вдоль одной прямой, которая является касательной к получившейся кривой.

Кривая Безье лежит в выпуклой оболочке, создаваемой управляющими линиями. Это свидетельствует о стабильности ("благонравном поведении") кривой (рисунок 34).

Кривая Безье симметрична, т. е. она сохраняет свою форму, если изменить направление вектора кривой на противоположный ("поменять местами" начальную и конечную опорные точки). Это свойство находит свое применение при создании составных контуров.

Одной из самых важных причин выбора в качестве средств векторной графики кривых Безье и NURBS-кривых является управляемая гладкость. Гладкость означает, что при моделировании на кривой не образуется петель и резких преломлений (тем более разрывов). Но при этом, не исключена возможность создания, как гладкого сопряжения, так и изгибов, например острых углов.

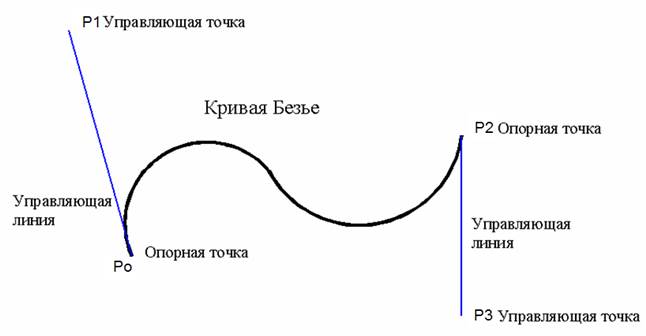
Рисунок 33

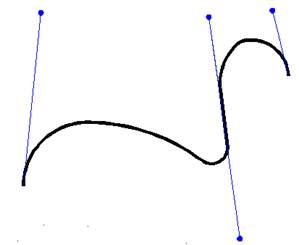
Рисунок 34

Кривая Безье, используя математический язык, "аффинно - инвариантна", т. е. она сохраняет свою форму при масштабировании (рисунок 35). Это свойство является фундаментом свободы манипулирования объектами векторной графики.

Если существует только две контрольных точки (опорных точки) или управляющие линии коллинеарны (лежат на одной прямой), кривая превращается в прямой отрезок.

Изменение положения хотя бы одной из контрольных точек ведет к изменению формы всей кривой Безье. Это свойство - источник бесконечного разнообразия форм векторных объектов. Из множества таких элементарных кривых составляется контур произвольной формы и произвольной сложности.

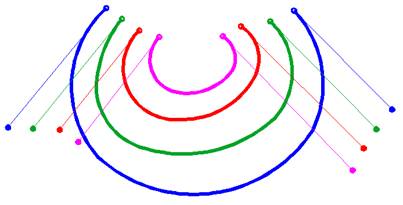
Рисунок 35

Термин NURBS, который является аббревиатурой (сокращением) и расшифровывается как Non-Uniform Rational B-spline, где:

"Non-Uniform" (неоднородный) означает, что область влияния контрольной точки на форму кривой может быть различной. Это очень важное свойство для моделирования иррегулярных кривых.

"Rational" (рациональный) означает, что математическое выражение, описывающее форму моделируемой кривой, есть отношение двух полиномов. Эта особенность позволяет точнее моделировать различные кривые, например конические сечения.

"B-spline" (basis spline, базовый сплайн) - способ математического описания кривой интерполяцией между тремя и более контрольными точками.

Заметим что, привычные для плоских векторных художников кривые Безье являются специальным (частным) случаем В-сплайна.

Одной из основополагающих особенностей NURBS-кривой является то, что ее форма определяется расположением множества контрольных точек. Контрольные точки соединены для наглядности прямыми линиями. Эта ломаная линия получила название управляющего многоугольника (control polygon), рисунок 36. Каждая контрольная точка определяет форму только той части кривой, которая находится в ее окрестности, и оказывает меньшее воздействие или вовсе не влияет на форму оставшейся части кривой.

Если веса всех контрольных точек положительны, кривая лежит в области, полученной соединением крайних (внешних) контрольных точек. Такой "габаритный" контейнер получил название "выпуклой оболочки" (convex hull).

Основными объектами ВГ являются: примитивы (линия, круг, эллипс и др.), составные объекты и различные заливки.

Примитив - объект создаваемый, редактируемый и уничтожаемый одной командой.

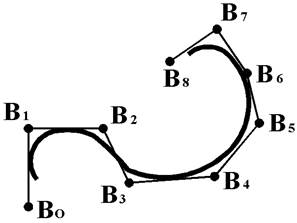
Рисунок 36

Сегменты могут иметь прямолинейную или криволинейную форму. Форма сегмента определяется типом ограничивающих его узлов, которые могут быть гладкими или угловыми. В гладком узле контур образует плавный перегиб, в то время как в угловом — из­лом. Если сегмент хотя бы с одной стороны будет ограничен глад­ким узлом, он будет криволинейным. С другой стороны, чтобы сегмент был прямолинейным, он должен быть ограничен с обеих сторон только угловыми узлами. Различают также еще два типа узлов. Узел Безье – вершина подобная гладкой вершине, но позволяющая управлять кривизной сегментов при входе и выходе из нее. Для этого она снабжается касательными векторами с маркерами (квадратиками) на концах. У вершин Безье касательные вектора всегда лежат на одной прямой, а расстояние маркеров от вершины можно изменять. При этом перемещение одного маркера приводит к центрально-симметричному перемещению другого. Вершина Безье с изломом – отличатся тем, что касательные векторы не связаны друг с другом, и маркеры можно перемещать независимо.

Замкнутыеконтуры (например, многоугольные, эллиптические и т.п.) могут иметь заливку, т.е. их внутреннее пространство может быть заполнено произвольным цветом. Программы иллюстрирова­ния способны поддерживать не только сплошные, но и более слож­ные типы заливок - градиентные(плавный переход от одного цвета к другому) или узорные(заливка повторяющимся рисунком). Некоторые программы позволяют создавать текстур­ные заливки, т.е. заливки редактируемыми рисунками, похожими на какие-либо материалы.

Любые контуры могут иметь обводку. Контур - понятие мате­матическое, и толщины он не имеет. Чтобы сделать контур видимым, ему придают обводку — линию заданной толщины и цвета, проведенную строго по контуру. По умолчанию всем новопостроенным линиям задается одинаковая толщина, однако по желанию обводку можно изменить - создать пунктирную, гради­ентную или художественную.

Соотношение цвета и формы в растровой графике можно определить следующим образом:

- цвет и форма неотделимы;

- цвет первичен;

- форма - производное от цвета;

- в чистом виде форма не существует.

Процесс создания изображений точечной графики, если не считать компьютерной специфики, практически идентичен работе художника, который за счет расположения на плоскости мазков краски создает иллюзорную действительность — метафору пространства.

При редактировании векторной графики изменяется в первую очередь форма объекта, а цвет играет второстепенную роль. Соотношение цвета и формы в векторной графике можно определить следующим образом:

- цвет и форма независимы друг от друга;

- форма первична;

- цвет - просто заполнитель формы;

- в чистом виде цвет не существует.