Медиана и мода.
Достоинством средней как обобщающего показателя является то, что она одной величиной характеризует целую совокупность разных величин. Но для всесторонней характеристики совокупности, как и для решения некоторых практических задач, нужны и такие обобщающие показатели, которые характеризуют особенности распределения единиц совокупности по величине изучаемого признака. К таким показателям относятся медиана и мода, которые называются распределительными средними. Последние относятся к средним потому, что они привлекаются и для определения типических характеристик совокупности, несмотря на то, что типичность этих характеристик отличатся от типичности других средних.
Медиана (Ме) – значение изучаемого признака, которое по своей величине занимает серединное место в ряду вариантов, расположенных в порядке их возрастания или убывания. Такой ряд называется ранжированным. Примером такого ряда может служить месячная заработная плата рабочих цеха.
| Порядковый номер рабочего | Итого | |||||||
| Месячная заработная плата, руб |
В этом ряду среднее место по размеру заработной платы занимает рабочий с номером 4, получивший 160 руб. эта величина и есть медиана. Меньше и больше медианы одинаковое число вариантов. При нечетном числе вариантов п порядковый номер, которому соответствует медиана, определяется по формуле:
п +1 7 +1
NMe = --------- = --------- = 4.
2 2
когда количество вариантов в ряду четное число, медианой считают один из тех вариантов, который по своей величине мог бы находиться посередине между вариантами с номером п/2 и (п + 2)/2.
Так, если бы в цехе был еще и восьмой рабочий с заработной платой 276 руб., то медиана находилась бы посередине между четвертым и пятым порядковыми номерами. В таких случаях принято считать, что в промежутке между номерами п/2 и (п + 2)/2 идет равномерное нарастание или убывание вариантов. Поэтому за медиану принимают среднюю арифметическую из вариантов с номерами п/2 и (п + 2)/2. В данном примере Ме = (х4 +х5) / 2 = (160+175) / 2 = 167,5 руб.
Смысл полученного результата такой: одна половина рабочих получила за месяц меньше, а другая – больше 167,5 руб. Медиана, следовательно, обобщающий показатель распределения совокупности, уровень признака, который делит совокупность на две равные части, и представляет обычно интерес в анализе.[3]
Медиана, кроме того, обладает свойством линейного минимума: сумма абсолютных значений отклонений от величины признака у всех единиц совокупности от медианы минимальна, т.е.
∑ | xi – Me| = min и ∑ | xi – Me| fi = min.
Это свойство имеет важное значение для решения некоторых практических задач, например расчета самого короткого пути из всех возможных для транспорта, размещения точек обслуживания населения таким образом, чтобы расстояние, проходимое жителями, обслуживаемыми данной точкой, было наименьшим и т.п.
Медиана в отличие от средней не является абстрактной величиной. Она находится точно в середине ряда, представляет собой реальное значение признака, соответствует определенному варианту и при этом наиболее точна в случае нечетного числа членов совокупности. Медиана как обобщающая характеристика совокупности не может, однако, заменить среднюю. Медиана – это центр распределения численности единиц совокупности, а средняя – центр распределения отклонений значений признака от равнодействующей. Величина медианы определяется лишь одним или двумя серединными значениями признака. Изменения всех остальных величин, если они не меняют последовательности членов в центре ряда, не находят отражения в медиане. Так, если в примере месячную заработную плату поднять на 40 руб., это не скажется на медиане, несмотря на то, что тем самым значительно повышаются доходы двух рабочих цеха и существенно выравнивается заработная плата членов коллектива. Поэтому медиана, представляющая определенный интерес в анализе, не может заменить среднюю, которая при замене реального коллектива абстрактным коллективом с уравненными признаками оставляет неизменным определяющий показатель совокупности.
 Медиана же не связана с определяющим показателем, она может быть больше и меньше средней и не может выполнять функции средней, т.е. пМе = ∑хi . в нашем примере фонд заработной платы восьми рабочих цеха составил: 1148 + 276 = 1424 руб., а средняя заработная плата: 1424 / 8 = 178 руб. Медиана же равна 167,5 руб,, а 167,5 * 8 = 1340 руб., а не 1424 = 178 * 8.
Медиана же не связана с определяющим показателем, она может быть больше и меньше средней и не может выполнять функции средней, т.е. пМе = ∑хi . в нашем примере фонд заработной платы восьми рабочих цеха составил: 1148 + 276 = 1424 руб., а средняя заработная плата: 1424 / 8 = 178 руб. Медиана же равна 167,5 руб,, а 167,5 * 8 = 1340 руб., а не 1424 = 178 * 8.
Не умаляя значения медианы в анализе, отметим, что она все же не основная, а дополнительная характеристика совокупности. Основной характеристикой является средняя величина. Лишь при решении некоторых задач, особенно связанных с определением оптимума, совпадающего с вариантом, приходящимся на середину ряда, медиана имеет самостоятельное значение. Медианой целесообразно пользоваться, когда неизвестны границы открытых крайних интервалов вариационного ряда, на которые приходится значительная часть единиц всей совокупности, так как средняя в этих случаях страдает значительной неточностью.
Медиана правильнее отражает типичный уровень признака в неоднородной совокупности, чем средняя величина. Если значение признака составляет:114, 119, 127, 140, 148 и 296, то медиана равна 129, а средняя арифметическая – 1073 / 7 = 153,3. Шесть значений признака из семи меньше средней, поэтому она плохо отражает типичный размер признака.
Приведенные примеры вычисления медианы относятся к случаю, когда расчет производится на основе индивидуальных значений признака. Обычно же в статистике приходится иметь дело со сгруппированными данными в форме дискретных и интервальных рядов. Расчет медианы для интервальных радов покажем в таблице 15, где дана группировка колхозов области по надою молока от одной коровы.
| Сначала необходимо определить медианный интервал. Для этого пользуются рядом накопительных частостей, образуемым путем последовательного суммирования частот, начиная от первого интервала. В приведенном примере на первые три группы колхозов, в которых удойность коров | Таблица 15. | |
| Распределение колхозов области по надою молока от одной коровы | ||
| Удойность в среднем от одной коровы за год, кг | Процент колхозов | Ряд накопленных частостей |
| До 1000 | 7,6 | 7,6 |
| От 1000 – 1650 | 9,7 | 17,3 |
| 1650 – 2000 | 16,1 | 33,4 |
| 2000 – 2500 | 37,5 | 70,9 |
| 2500 – 3000 | 20,6 | 91,5 |
| 3000 – 4000 | 8,2 | 99,7 |
| 4000 и выше | 0,3 | |
| Х |
меньше 2000 кг, приходится 33,4% всех колхозов, т.е. меньше половины на 16,6%, а на первые четыре группы – 70,9%, те больше половины. Следовательно, медиана находится внутри четвертого интервала с границами 2000 – 2500 кг. На этот интервал в 500 кг приходится 37,5 % колхозов, из которых 16,6% надо прибавить к первым трем группам для того, чтобы всю совокупность колхозов разделить пополам. Исходя из предположения, что в пределах медианного интервала частоты или частости распределяются равномерно, определяют, какая часть интервала приходится на 16,6% колхозов.
16,6
Она в данном примере равна: 500 * --------- = 220 кг. Следовательно, медиана
37,5
равна: 2000 + 220 = 2220 кг.
Формула этого расчета в общем виде такая:
∑ f 100
----- - Sm – 1 ----- - 33.4
2 2
Ме = xe + h ---------------- =2000 + 500 --------------- = 2000 + 500 * 0.44 = 2220 кг,
fm 37.5
где хе – нижняя граница медианного интервала; h – величина медианного интервала; ∑f –сумма частот или частостей ряда; S m – 1 - сумма накопленных частот в интервалах, предшествующих медианному; fm – частота медианного интервала. Полученный по этой формуле результат означает в данном примере, что в половине колхозов области удойность не превышала 2220 кг, а в половине была выше этого уровня.
Такой расчет для дискретных рядов является в определенной мере условным, так как медиана не может находиться между двумя прерывными значениями признака. Например, не может медиана находиться в интервале между тремя и четырьмя в распределении семей по числу совместно проживающих членов семей и составлять, допустим, 3,47.
Несмотря, однако, на условность такого результата, означающего, что размер одной половины семей не превышает 3,47 человек, а второй – превышает эту цифру, все же сопоставление подобных результатов во времени и пространстве не лишено смысла. По нему можно судить о динамике и географии размера семьи.
Важной характеристикой центра распределения является и мода. Мода (Мо) – это вариант признака, который при данном сочетании причин разного порядка чаще всего встречается в вариационном ряду. Например, цена, по которой чаще всего реализуется данный товар на рынке, является модой или модальной ценой. Месячная заработная плата, которая чаще встречается в данном коллективе, является для него модальной заработной платой. Мода отвечает на вопрос о том, какое значение изучаемой переменной величины наиболее вероятно. То, что в статистике принято называть модой, считается в обычной жизни массовым, типичным, типическим.
В связи с этим не следует смешивать емкое понятие «типичное», принятое в обычной жизни, в литературе и философии, с аналогичными, более дифференцированными понятиями в статистике. «Типическое или типичное (от греческого слова «образец»)—нормальное, образцовое, наиболее вероятное для данной конкретной системы объективного мира».[4] В статистике, которая свои понятия переводит на язык счетных категорий и выражает их в обобщающих количественных показателях, характеризующих социально-экономические явления в единстве с их качественной определенностью, понятиям «нормальное», «наиболее вероятное» и «образцовое» соответствуют три разных обобщающих показателя: средняя, мода и индивидуальное — передовое.
Средняя — величина, типичная для всех единиц однородной совокупности и для совокупности в целом. Мода — тоже типичная величина, но в том смысле, что она встречается в совокупности или объективно может встретиться чаще других. Она имеет важное значение для решения некоторых задач, например, какой высоты должны быть предназначенные для массового потребления станки, столы и т. п., какое количество детей чаще всего встречается в семье, какое время дня является «пиковым» для работы предприятий общественного питания, электростанций, городского транспорта и др., какой уровень выполнения плана наиболее часто встречается в том или ином коллективе рабочих или предприятий и т. п. Индивидуальное, передовое — типичная величина, характеризующая с количественной стороны только зародившееся явление, но прогрессивное, совершенное, образцовое, таящее в себе тенденцию развивающегося, перспективного, которое со временем станет массовым.

 Поэтому, когда говорят о типичности средней, моды и индивидуального— передового, имеют в виду, по существу, разные понятия. В частности, говоря о типичности моды, следует учесть, что она в отличие от средней характеризует размер признака, свойственный хотя и значительной части, но не всей совокупности. Поэтому и мода не может выполнять функцию замены — x ∑f = ∑xf ,а Мо∑f = ∑ xf. Степень типичности моды зависит от формы распределения совокупности по величине изучаемого признака. Чем большая часть совокупности приходится на модальное значение переменной, т. е. чем острее вершина кривой распределения, тем типичнее мода. Средняя же как равнодействующая типична в любой однородной, совокупности. Она и более устойчива, так как определяется значениями всех членов совокупности. Мода же зависит только от значения наибольшей частоты. Кроме того, в выборочных обследованиях, широко применяемых в статистике, вероятная ошибка средней арифметической везде поддается оценке, а моды — лишь в распределениях особого рода.
Поэтому, когда говорят о типичности средней, моды и индивидуального— передового, имеют в виду, по существу, разные понятия. В частности, говоря о типичности моды, следует учесть, что она в отличие от средней характеризует размер признака, свойственный хотя и значительной части, но не всей совокупности. Поэтому и мода не может выполнять функцию замены — x ∑f = ∑xf ,а Мо∑f = ∑ xf. Степень типичности моды зависит от формы распределения совокупности по величине изучаемого признака. Чем большая часть совокупности приходится на модальное значение переменной, т. е. чем острее вершина кривой распределения, тем типичнее мода. Средняя же как равнодействующая типична в любой однородной, совокупности. Она и более устойчива, так как определяется значениями всех членов совокупности. Мода же зависит только от значения наибольшей частоты. Кроме того, в выборочных обследованиях, широко применяемых в статистике, вероятная ошибка средней арифметической везде поддается оценке, а моды — лишь в распределениях особого рода.
В дискретных рядах мода легко определяется как вариант, которому соответствует максимальная частота. Определение моды в интервальных рядах требует расчета. Наибольшее распространение получила методика расчета, предложенная известным статистиком Р.М. Орженцким (1863— 1923). Сначала находят интервал, обладающий наибольшей частотой. Этот интервал называется модальным. Затем находят приближенное значение модальной величины признака по формуле
fm – fm-1
Mo = xo + h ----------------------------------,
(fm – fm-1) + (fm – fm+1) 
где хo — нижняя граница модального интервала; h — величина модального интервала; fm — частота модального интервала; fm+1 — частота интервала, следующего за модальным; fm-1 — частота интервала, предшествующего модальному.
Например, в таблице 15 модальный интервал составляет 2000—2500 кг, так как ему соответствует наибольшая частота 37,5%, нижняя его граница х0=2000, а величина интервала h =500.
Следовательно, 37,5 – 16,1
Мо = 2000 + 500 ------------------------------------ = 2280 кг.
(35,7 – 16,1) + (37,5 – 20,6)
Это значит, что чаще всего встречаются колхозы, у которых надой в среднем от одной коровы составляет 2280 кг.
При такой методике определения в моде, если совокупность достаточно большая, находит отражение тип распределения. Мода относится к тому варианту в модальном интервале, которая делит его пропорционально быстроте нарастания или убывания частот в смежных интервалах. Так, если бы в нашем примере распределение было симметричным, следовательно, разности fm - fm-1 и fm – fm+1 были бы одинаковы и равны α, тогда
α 1
Мо=2000 + 500 —— =2000 + 500 — = 2250, т. е. совпала бы с серединой
α + α 2
модального интервала. В действительности же, если судить по трем максимальным частотам, имеет место левосторонняя асимметрия, поэтому мода несколько больше середины модального интервала. Для решения практических задач наибольший интерес представляет мода, выраженная в виде интервала, а не дискретным числом. Объясняется это назначением моды, которая должна выявить наиболее распространенные размеры явления. Выраженная в виде дискретного числа мода часто не отвечает этому требованию. Так, в нашем примере процент колхозов, в которых годовой надой в среднем на одну корову составляет 2280 кг, хотя и больше, чем процент колхозов с любым другим уровнем надоя, но сам по себе этот процент может быть небольшим. Процент колхозов же с удойностью в пределах интервала 2000—2500 кг — 37,5, а 2000—3000 кг — 58,1, т. е. весьма значителен.
Хотя средняя, медиана и мода по-разному определяются и отвечают на разные вопросы, но это не значит, что они независимы друг от друга и могут резко отличаться по величине в качественно однородной совокупности.

 К. Пирсон, впервые введший понятие моды, установил, что в большинстве асимметричных распределений расстояние от медианы до средней арифметической приблизительно равно половине расстояния от медианы до моды. Степень различия между ними зависит от характера взаимосвязей между основными, внутренними и внешними случайными причинами. В тех случаях, когда эти взаимосвязи приводят к симметричному распределению, средняя, медиана и мода совпадают. В асимметричных распределениях эти три обобщающие характеристики различны, причем в правосторонней асимметрии х > Ме > Мо, а в левосторонней х < Ме < Мо. Соотношение между этими характеристиками в симметричном и асимметричном распределении показано на рис. 9.1.
К. Пирсон, впервые введший понятие моды, установил, что в большинстве асимметричных распределений расстояние от медианы до средней арифметической приблизительно равно половине расстояния от медианы до моды. Степень различия между ними зависит от характера взаимосвязей между основными, внутренними и внешними случайными причинами. В тех случаях, когда эти взаимосвязи приводят к симметричному распределению, средняя, медиана и мода совпадают. В асимметричных распределениях эти три обобщающие характеристики различны, причем в правосторонней асимметрии х > Ме > Мо, а в левосторонней х < Ме < Мо. Соотношение между этими характеристиками в симметричном и асимметричном распределении показано на рис. 9.1.
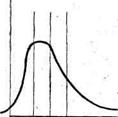
х>Ме>мо х=Мо=№ х<ме<Мо
1 2 3
Рис. 9.1. Соотношения между средней, модой и медианой:
1 — правосторонняя асимметрия; 2 — симметричная кривая; 3 — левосторонняя асимметрия
В умеренно асимметричном распределении медиана находится между средней арифметической и модой приблизительно на расстоянии одной трети по шкале х-ов. Для распределения такого типа характерно следующее приближенное соотношение

 Мо ≈ х – 3 ( х – Ме),
Мо ≈ х – 3 ( х – Ме),
или

 х ≈ Мо – 3 ( х - Ме).
х ≈ Мо – 3 ( х - Ме).
Из этого следует, что сочетание моды, медианы и средней важно и для характеристики типа распределения.
[1] Исключение составляет средняя из относительных величин, характеризующих динамику явления за ряд лет или других периодов. В этом случае применяется средняя геометрическая.
[2] Если обе части равенства fx = v поделить на v, получим (f / fx) * x = 1 или (1/х) * х = 1
[3] Интерес представляют и уровни признака, делящие совокупность на 4 части (квартили), на 10 частей (децили), на 100 частей (перцентили), но эти уровни по своей сущности не могут быть отнесены к средним величинам. Исчисляются они по тому же принципу, что и медиана.
[4] Философская энциклопедия, т. 5. М., Советская энциклопедия, 1970, с. 233.
Дата добавления: 2015-04-29; просмотров: 1758;
