Способы дополнения однокартинного чертежа
Способ с числовыми отметками.Суть способазаключается в том, что недостающая в плоскости проекций пространственная координата отмечается на чертеже числом. Этот способ широко применяется в топографии, при пост-роении профиля дорог, в том числе железнодорожного пути.
Способ академика Федорова. Принципиальное отличие от предыдущего способа состоит в том, что числовые отметки заменяются масштабными отрезками. Способ в основном применяется в кристаллографии.
Способ составления аксонометрических проекции применяют в строительных и машиностроительных чертежах в основном для наглядного изображения предмета.
Способ составления комплексного чертежа наиболее широко применяется при составлении строительных и машиностроительных чер-
тежей.
2. ТОЧКА, ПРЯМАЯ И ПЛОСКОСТЬ НА КОМПЛЕКСНОМ
ЧЕРТЕЖЕ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ
Прежде чем перейти к изображению геометрических элементов на комп-лексном чертеже, рассмотрим положение некоторой точки А в пространственной системе координат – X, Y, Z (рис. 2.1).
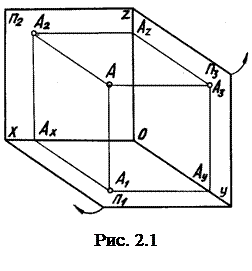 Спроецируем ортогонально точку А на три взаимоперпендикулярные плоскости проекций П1,П2,П3 и получим проекции этой точки: А1 – горизонтальная; А2 – фронтальная,
Спроецируем ортогонально точку А на три взаимоперпендикулярные плоскости проекций П1,П2,П3 и получим проекции этой точки: А1 – горизонтальная; А2 – фронтальная,
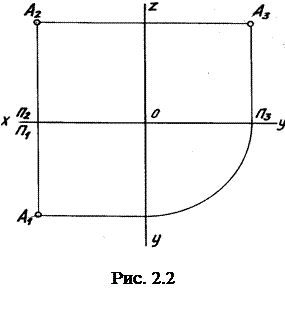
А3 – профильная. Координаты Аx, Ay, Az определяют положение этой точки в пространстве. Такое наглядное изображение точки, находящейся в пространстве, дает представление о расположении точки относительно плоскостей проекций П1, П2, П3. Однако в этом случае искажаются действительные размеры в системе координат и, самое главное, затрудняется чтение чертежа при изображении сложных предметов. Французский геометр Г. Монж предложил перейти от такого изображения предмета к комплексному чертежу. Комплексный чертеж – это ортогональное изображение предмета на две или более взаимоперпендикулярные плоскости проекций, совмещенные с плоскостью чертежа. Это совмещение происходит следующим образом: плоскости П1 и П3 поворачиваются относительно осей X и Z до положения,
когда они составляют одну плоскость с П2 (рис. 2.2).
На таком комплексном чертеже точка будет изображаться своими проекциями. Чтобы точка на чертеже была задана, достаточно иметь две ее проекции. Размеры представляются на комплексном чертеже в натуральную величину. Предмет можно изучать спереди, сверху, слева, но при этом необходимо иметь навыки пространственного представления на таком чертеже.
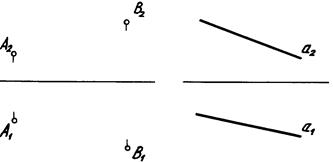
Прямая на комплексном чертеже может быть задана двумя точками или своими проекциями. Минимальное количество проекций прямой на чертеже – две (рис. 2.3).
а б
Рис. 2.3
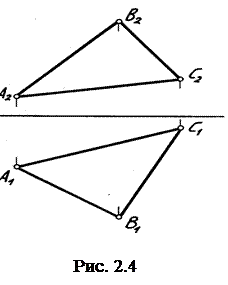 Плоскость на комплексном чертеже может быть задана тремя точками, точкой и прямой, двумя пересекающимися прямыми, двумя параллельными прямыми, плоской геометрической фигурой (треугольник, окружность и т. д.) и др. Плоскость на комплексном чертеже определяют две ее проекции (рис. 2.4).
Плоскость на комплексном чертеже может быть задана тремя точками, точкой и прямой, двумя пересекающимися прямыми, двумя параллельными прямыми, плоской геометрической фигурой (треугольник, окружность и т. д.) и др. Плоскость на комплексном чертеже определяют две ее проекции (рис. 2.4).
3. ПРЯМЫЕ И ПЛОСКОСТИ ОБЩЕГО И ЧАСТНОГО ПОЛОЖЕНИЯ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ
Дата добавления: 2015-04-29; просмотров: 1612;
