Задание 4. Дифракция Фраунгофера наблюдается в параллельных лучах
ИЗУЧЕНИЕ ДИФРАКЦИИ ФРАУНГОФЕРА
Дифракция Фраунгофера наблюдается в параллельных лучах. Часто для удобства наблюдения используют собирающую линзу и получают дифракционную картину в фокальной плоскости линзы.
Схема установки для наблюдения дифракционной картины изображена на рис. 1.
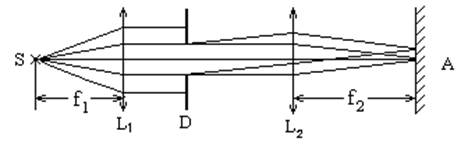
Рис. 1
Источник света S находится в фокусе линзы L1 .На экран D с отверстием – диафрагмой в виде щели падает параллельный пучок. Если бы не было явления дифракции, т.е. свет не огибал бы препятствие, то на экране А после фокусировки линзой L2 было бы изображение освещенной щели. За счет огибания световыми волнами краев щели на экране А получаются чередующиеся изображения щели в виде светлых и темных полос, т.е. в фокальной плоскости линзы L2 наблюдается дифракционная картина. Вид картины зависит от размеров диафрагмы, ее формы и длины волны падающего света.
а) Дифракция на одной щели
На щель шириной а падает параллельный пучок света, его волновой фронт – плоскость (рис. 2). Разобьем щель на зоны Френеля. Пусть АА' – ширина одной зоны Френеля. Тогда, с одной стороны,
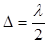 (1)
(1)
по условию Френеля, а, с другой стороны, из треугольника АА' В
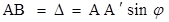 . (2)
. (2)
Число зон, которое укладывается в щели шириной а, определяется как
 . (3)
. (3)

Рис. 2
Из (1), (2) и (3) получим 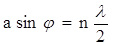 .
.
Если n = 2k, т.е. в отверстии щели укладывается четное число зон, то при наложении все вторичные волны гасят друг друга, получается условие минимума:
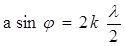 , (4)
, (4)
где k = 1, 2, 3,...
Если n = (2k + 1), т.е. число зон нечетное, то действие щели эквивалентно действию одной зоны Френеля, будет наблюдаться свет, т.е. получается условие максимума при дифракции от одной щели:
 , (5)
, (5)
где k = 0, 1, 2,....
Рассмотрим изменение интенсивности света на экране, расположенном в фокальной плоскости линзы. Минимум интенсивности света будет наблюдаться под углами:
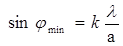 ,
,
где k = 1, 2, 3,...
Для различных значений k sinφmin будет иметь значения: 
Максимум интенсивности света будет наблюдаться под углами:
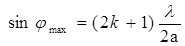 ,
,
где k = 0, 1, 2,...
Для различных значений k sinφmax будет иметь значения:
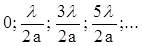
Графически зависимость интенсивности света от значения sinj будет выглядеть так, как показано на рис.3.
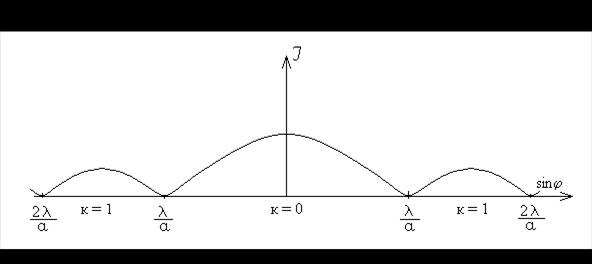
Рис. 3
На рис. 3 видно, что на экране будут наблюдаться чередующиеся максимумы и минимумы интенсивности света. Они будут иметь вид светлых и темных полос, параллельных щели. Поскольку на рис.2 дано сечение щели, то на экране в точке С показано сечение одной из таких полос.
Существуют формулы, которые дают возможность подсчитать величину интенсивности в максимумах нулевого, первого и второго порядков.
б) Дифракция на N -щелях
Дифракционной решеткой называется совокупность большого числа одинаковых, отстоящих друг от друга на одно и то же расстояние щелей. Расстояние с = а + в называется постоянной или периодом решетки.
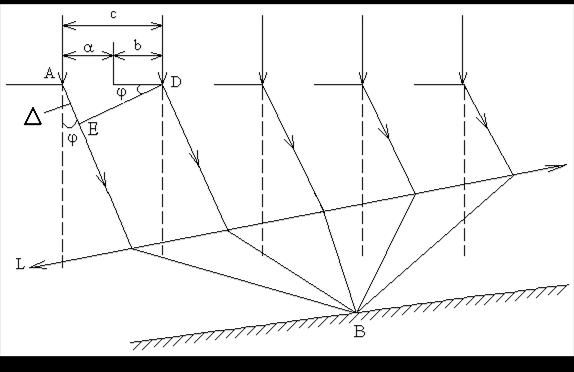 |
Рассмотрим частный случай: пусть а = в, т.е. с = 2а, число щелей N = 4. Каждая из щелей даст на экране картину, описываемую предыдущим графиком (рис. 3) для одной щели. Если бы колебания, приходящие в точку В (рис. 4) от различных щелей, после фокусировки линзой L были некогерентны, то результирующая картина от 4 щелей отличалась бы от картины, создаваемой одной щелью, (рис. 3) лишь тем, что все интенсивности возросли бы в 4 раза. Однако, колебания от различных щелей являются когерентными, поэтому для нахождения результирующей интенсивности нужно найти фазовые соотношения при сложении волн, приходящих от разных щелей (когерентных источников), т.е. теперь уже, кроме явления дифракции от одной щели, нужно учитывать явление интерференции от 4-х щелей (рис. 4).
Рис. 4
Очевидно, что минимум, полученный от каждой щели, будет на прежнем месте на экране, так как под этим углом в каждой щели укладывается четное число зон Френеля, и ни одна из щелей не пошлет в этом направлении свет. Поэтому условие (4) одновременно является и условием основного минимума для решетки.
Параллельные лучи, проходящие через щели под любыми другими углами, кроме углов, удовлетворяющих условию (4), будут посылать свет на экран, при этом они будут интерферировать. (Помним, что на рис.4 – сечение решетки, на самом деле свет фокусируется линзой не в точку, а в полосу). Волны будут усиливать друг друга, если разность хода между ними будет кратна l, разность фаз Dφ = 2kπ. Условие усиления света при интерференции будет иметь вид:
с sinj = kl , (6),
где k = 0, 1, 2,...,
Разность хода между лучами, принадлежащими разным щелям, обозначим через D. Из рассмотрения треугольника АДЕ (рис. 4) имеем:
D = АЕ = АД sinj,
где D = kl, АД = с - постоянная решетки.
Условие (6) – условие возникновения главных максимумов. Амплитуда колебаний в соответствующей точке экрана увеличится. Формула (6) определяет положения максимумов интенсивности, называемых основными или главными. Число k дает так называемый порядок главных максимумов. Максимум нулевого порядка только один, максимумы первого, второго и т.д. порядков расположены по обе стороны от нулевого. В промежутке между соседними главными максимумами имеется по (4-1) добавочных минимумов, которые возникают в тех направлениях, для которых колебания от отдельных щелей взаимно гасят друг друга. Направления добавочных минимумов определяются условием:
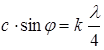 (7),
(7),
где k = 1, 2, 3,...,
кроме k = 0, 4, 8, 12,..., т.е. кроме тех условий, при которых условие (7) переходит в условие (6).
Между дополнительными минимумами располагаются слабые вторичные, добавочные максимумы. Число таких максимумов, приходящееся на промежуток между соседними главными максимумами, равно (4-2). Дополнительные максимумы возникают за счет того, что волны, приходящие в данное место экрана, усиливаются волнами не от всех щелей, а только от некоторых. Например, если между волнами, приходящими от двух соседних щелей разность хода равна 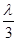 , то между волнами от первой и четвертой щели разность хода становится равной l, и волны усиливают друг друга, возникает добавочный максимум. Соответствующий расчет показывает, что интенсивность вторичных максимумов не превышает 1/23 интенсивности ближайшего главного максимума.
, то между волнами от первой и четвертой щели разность хода становится равной l, и волны усиливают друг друга, возникает добавочный максимум. Соответствующий расчет показывает, что интенсивность вторичных максимумов не превышает 1/23 интенсивности ближайшего главного максимума.
Таким образом, дифракционная картина, получающаяся от 4-х щелей, определяется условиями (4), (6), (7). Распределение интенсивности света на экране для этого случая представлено на рис. 5.
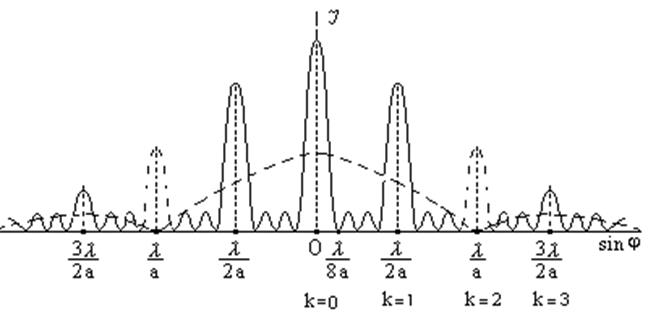 Рис. 5
Рис. 5
Подведем итоги. Основные минимумы наблюдаются под углами, для которых sinj имеет следующие значения:

Главные (основные) максимумы – под углами, для которых sinj имеет значения (помним, что нами выбрана решетка, у которой с = 2а):
 0;
0; 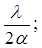
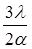
Для добавочных минимумов:
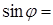
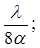
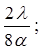

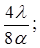
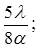
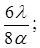
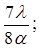
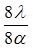
Главные максимумы при k = 2 и k = 4 не наблюдаются, так как мы задали условие: а = в и с = 2а, поэтому при k = 2 и k = 4 условие (6) переходит в условие (4), при котором в каждой щели укладывается четное число зон Френеля. Если число щелей N, то условие (7) запишется в виде:
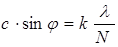 , (7’)
, (7’)
где k = 1, 2, 3,… кроме k = N, 2N, 3N,…,
когда условие (7) переходит в условие (6). При этом между главными максимумами будет (N-1) добавочных минимумов и (N-2) добавочных максимумов.
Если а<<c, то между основными минимумами может располагаться значительное количество основных максимумов. Количество наблюдающихся максимумов определяется из условия (6) при sinj ® 1.
Тогда номер последнего наблюдаемого максимума равен:
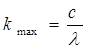 . (8)
. (8)
С увеличением числа щелей растет интенсивность главных максимумов, так как возрастает количество пропускаемого решеткой света. Однако, самое существенное изменение, вносимое большим числом щелей, состоит в превращении расплывчатых максимумов в резкие узкие максимумы, разделенные практически темными промежутками, ибо вторичные максимумы очень слабы: самый сильный из наблюдаемых вторичных максимумов составляет не более 5% интенсивности от главного.
Спектр, даваемый дифракционной решеткой, является равномерным по сравнению с дисперсионным, т.е, ширина каждого участка спектра приблизительно одинакова. В дисперсионном спектре длинноволновая часть спектра растянута по сравнению с коротковолновой. Из условия (6) cледует, что при освещении решетки немонохроматическим светом на экране вместо монохроматических светлых полос будут видны спектры, разделенные темными промежутками, причем расположение цветов в спектре будет таким: ближе к нулевому - фиолетовый цвет, крайний - красный. Чем больше постоянная дифракционной решетки, тем большее число спектров можно наблюдать и тем более узкими становятся отдельные спектральные линии. Дифракционная решетка обычно характеризуется числом штрихов на единицу длины - N0 , которое связано с постоянной решетки соотношением
 . (9)
. (9)
В 1785 г. дифракционную решетку изготовил Риттенгауз, но использована она не была. В 1821 году вновь была открыта Фраунгофером.
В настоящее время изготавливаются дифракционные решетки, у которых на 1 мм наносится 1200 штрихов и более.
В спектральном анализе дифракционная решетка используется для разложения света на составные цвета. С ее помощью можно определять спектральный состав света, поскольку соотношение (6) дает возможность по известному периоду дифракционной решетки (или числу штрихов на единицу длины) и экспериментально измеренному углу вычислить длину волны излучения.
Дифракционный спектр может наблюдаться только для длин волн, меньших постоянной решетки. Если l > с, то условие (6) может быть выполнено лишь для к=0. В этом случае дифракционная решетка не разлагает свет в спектр, а просто пропускает его в направлении падения.
 |
В последнее время стали применяться отражательные решетки (рис. 6). Тонкий слой металла определенного профиля наносится на стеклянную подложку, отполированную с оптической точностью. Наносимый металл имеет коэффициент отражения 88-95%. Интенсивность максимумов разных порядков приблизительно одинаковая. Такие решетки содержат от 3600 штрихов на 1 мм и более.
Рис. 6
МЕТОДИКА ИЗМЕРЕНИЙ
Наблюдение и исследование дифракции Фраунгофера на различных объектах проводится на установке (рис. 7),
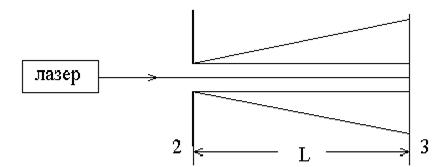
Рис. 7
состоящий из:
1 – лазера ЛГН - 109
2 – объекта исследования
3 – экрана (на расстоянии 1,85 м от объекта).
В качестве объектов используются: три одиночные щели различной ширины [2-2], дифракционные решетки с различным числом щелей (2, 3, 4) [2-5].
I. Получение и расчет фраунгоферовых дифракционных картин
от различных щелей
Задание 1.Определить ширину щели.
На пути лазерного луча поочередно поместите щели различной ширины
[2-2], добейтесь на экране четкой дифракционной картины.
Из условия минимума для одной щели (4) определите ширину щели:
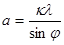 . (10)
. (10)
Для определения угла дифракции j измерьте расстояние h (рис.8) на экране между двумя минимумами первого порядка, а также расстояние L от щели до экрана.
Для малых углов 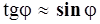 , тогда
, тогда 
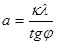 (11)
(11)
По результатам измерения h и L определите тангенс угла φ:
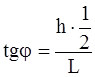 . (12).
. (12).
Следовательно: 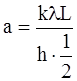 , (13)
, (13)
где а – ширина щели,
j – угол дифракции,
h – расстояние между двумя минимумами первого порядка,
L – расстояние от щели до экрана, в работе L = 1,85 м.
k = 1,
λ – длина волны лазера ЛНГ – 109, равная 630 нм.
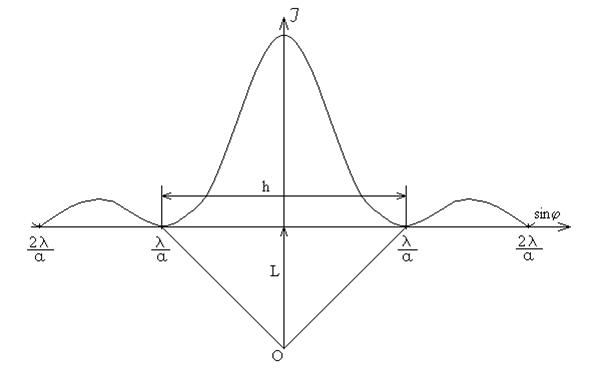
Рис. 8
Для каждой из трех щелей измерения произведите три раза. Результаты измерений и расчетов внесите в табл. 1.
Таблица 1
| Nщели | Nизмер | h, мм | Dh мм | а, мм | Dа, мм | 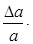 100 % 100 %
|
| cр. | ||||||
| cр. | ||||||
| cр. |
Для обработки полученных экспериментальных данных составлена программа на ЭВМ. Входные данные занести в табл. 2.
Таблица 2
| N щели | а |
Результаты табл. 2 введите в ЭВМ. По эталоным данным ЭВМ рассчитает и построит теоретическую зависимость интенсивности света от тангенса углов,
I = f(tgj) для одиночных щелей, а затем по Вашим измерениям. Из экспериментальных кривых видно, что с увеличением ширины щели уменьшается размер изображения щели, т.е., уменьшается угол дифракции, что соответствует теории.
II. Исследование дифракционных картин от дифракционных решеток,
содержащих 2, 3 и 4 щели [2-5]*
Задание 1.Определить ширину щели из условия основного минимума.
В экспериментальную установку (рис. 7) введите дифракционную решетку [2-5], содержащую две щели. Получите на листе бумаги, укрепленном на экране, расположенном от решетки на расстоянии L = 1,85 м, четкую дифракционную картину.** Распределение интенсивности света в зависимости от sinj для этого случая показано на рис. 9.
Точки АА удовлетворяют условию основного минимума (4).
Измерьте расстояние h (рис.9) между этими точками и по формуле (4), определите ширину щели, результаты внесите в табл. 3.
Выполняя каждое задание, проведите по 3 измерения, перемещая каждый раз лист с рисунком по вертикали.
Задание 2. Определить постоянную решетки из условия основного максимума.
На рис. 9 точки В1В1 соответствуют основным максимумам для k = 1. Эти максимумы получены за счет интерференции волн, идущих от всех щелей. Их наложение на оси sinj удовлетворяют условию основного максимума для решетки (6). Из этого условия можно определить постоянную решетки:
 . (14)
. (14)
 Рис. 9
Рис. 9
Таблица 3.
| L, м | Nизм. | h, мм | Dh, мм | tgj | а, мм | Dа, мм | 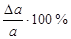
|
| 1.85 | |||||||
| Cред. |
Для определения sin j1 измерьте расстояние х (рис. 9) между точками В1 В1. Из формулы (15) определите sin j1:
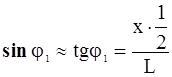 , (15)
, (15)
тогда 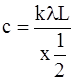 . (16)
. (16)
Результаты измерений и расчетов внесите в табл. 4.
Таблица 4
| L, м | Nизм. | x, мм | Dx мм | tgj | c, мм | Dc мм | 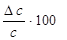 % %
|
| 1.85 | |||||||
| Сред. |
Задание 3.Определить постоянную решетки из условия добавочного минимума.
На рис. 9 точки D1D1 соответствуют добавочным минимумам. Их положение на оси sinj удовлетворяет условию добавочного минимума (7’).
Из этого условия можно определить постоянную решетки:

 (17)
(17)
Для нахождения sinj2 измерьте расстояние у. Значение sinj2 определите по формуле (18):
sinj2 » 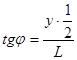 , (18)
, (18)
тогда:  . (19)
. (19)
где N - число щелей, в данном случае N = 2,
y - расстояние D1D1 при k = 1.
Результаты измерений и расчетов внесите в табл. 5.
Таблица 5
| L, м | Nизм. | y, мм | Dy2 мм | tgj2 | с, мм | Dс мм |  % %
|
| 1.85 | |||||||
| Cред. |
Задание 4.
В экспериментальную установку введите по очереди три и четыре щели. Пронаблюдайте дифракционную картину, объясните причину наблюдаемого распределения интенсивности света на экране. Обратите внимание на то, какие главные максимумы не наблюдаются, объясните почему это происходит.
Задание 5.Определить ширину щели и постоянную решетки, содержащей три щели.
В экспериментальную установку введите дифракционную решетку, содержащую три щели. Получите на экране (L = 1,85 м) четкую дифракционную картину. Распределение интенсивности света в зависимости от sinj в этом случае показано на рис. 10.
Точки АА удовлетворяют условию основного минимума (4).Точки В1В1 - удовлетворяют условию основного максимума (6). Точки D1D1 и D2D2 – удовлетворяют условию добавочных минимумов (7’), где N = 3; k = 1, 2, 4, 5.
Точки М1М1 соответствуют добавочным максимумам.
По формуле (13) определите ширину щели, для чего измерьте h.
По формуле (16) определите постоянную решетки, для чего измерьте х.
По формуле (19) определите постоянную решетки, для чего измерьте у и у1. Для решетки из трех щелей в формуле (19) возьмите N = 3, k выберите из возможных значений: k = 1, 2, 4, 5….
Результаты измерений и расчетов внесите в табл. 6., которую составьте сами по аналогии с предыдущими таблицами.
Задание 6. Определить ширину щели и постоянную решетки, содержащей четыре щели.
В экспериментальную установку введите дифракционную решетку, содержащую 4 щели. Получите четкую дифракционную картину. Распределение интенсивности света в зависимости от sinj в этом случае показано на рис. 11.
0 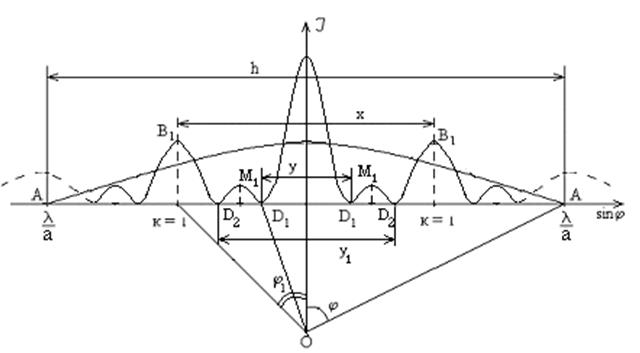
Рис. 10
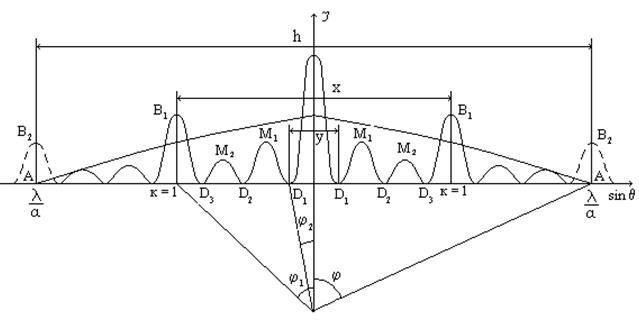
Рис. 11
Точки АА удовлетворяют условию основного минимума (4). Точки В1В1 – удовлетворяют условию основного максимума (6). Точки D1D1, D2D2 и D3D3 удовлетворяют условию добавочных минимумов (7’), где N = 4; k = 1, 2, 3, 5, 6, 7. Точки М1М1 и М2М2 – соответствуют добавочным максимумам.
Приведите измерения и расчеты, аналогичные описанным в задании 5. Результаты внесите в табл. 7, которую составьте сами.
* Все студенты выполняют задания 1-4. Задания 5 и 6 являются дополнительными, они выполняются по указанию преподавателя.
** На листе бумаги провести вертикальную ось, вдоль которой разместить картины для всех заданий, совмещая центр нулевого максимума с осью. На горизонтальных осях отмечать точки, соответствующие главным и добавочным минимумам и главным максимумам, при этом лист с рисунками нужно перемещать по вертикали.
| <== предыдущая лекция | | | следующая лекция ==> |
| Правила этикета и носовой платок. | | | Изучение оптических систем. |
Дата добавления: 2015-04-29; просмотров: 1297;
