Колебания материальной точки

Общим признаком всех колебательных движений является их многократная повторяемость через определенные промежутки времени. Колебательное движение материальной точки происходит при условии наличия восстанавливающей силы.

Восстанавливающая сила – сила, стремящаяся вернуть точку в положение равновесия.

Проекция восстанавливающей силы на ось Ox может быть найдена из выражения:

F_x = –c·x, (3.1)

где c – коэффициент пропорциональности.

Кроме восстанавливающей силы при колебаниях на точку может действовать также возмущающая сила, т. е. такая сила, которая зависит от времени. Обычно в качестве возмущающей силы рассматривают силу, проекция которой на ось Ox определяется следующим выражением:

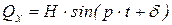, (3.2)

где H, p и δ – некоторые постоянные величины.

При колебаниях возникают силы сопротивления. Обычно эту силу рассматривают как функцию скорости движения точки и называют силой вязкого трения. При этом ее проекция на ось Ox определяется из выражения

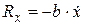, (3.3)

где b – коэффициент пропорциональности.

В зависимости от наличия восстанавливающей силы, возмущающей силы и силы сопротивления колебания материальной точки классифицируются следующим образом.

1) свободные колебания, при которых присутствует только восстанавливающая сила.

Дифференциальное уравнение свободных колебаний материальной точки имеет вид:

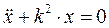. (3.4)

где k – циклическая (круговая) частота колебаний (число колебаний за 2π секунд).

При колебании груза на пружине циклическая частота может быть определена:

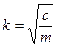. (3.5)

где с – жесткость пружины, m – масса груза

В случае свободных колебаний их период определится согласно выражению:

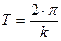, (3.6)

2) Свободные колебания при вязком сопротивлении (затухающие колебания) – это колебания при наличии восстанавливающей силы и силы сопротивления.

3) Вынужденные колебания возникают когда в колебательном процессе участвуют восстанавливающая и возмущающая силы.