магнитострикционным методом
Измерение модуля упругости твердых тел
3.1. Упругие свойства твердых тел
Модуль упругости (модуль Юнга) является одной из важнейших характеристик механических свойств твердых тел, его величина определяет способность тела подвергаться упругой деформации, сжатию или растяжению под воздействием внешних усилий.
 Деформация тел - это изменение его формы и размеров под действием внешних сил. Если после прекращения действия внешних сил прежние размеры и форма тела восстанавливаются, то такую деформацию называют упругой, в противном случае - пластической. Обычно при приложении к телу внешних сил сначала наблюдается упругая деформация, а затем, по мере роста этих сил, она может перейти в пластическую.
Деформация тел - это изменение его формы и размеров под действием внешних сил. Если после прекращения действия внешних сил прежние размеры и форма тела восстанавливаются, то такую деформацию называют упругой, в противном случае - пластической. Обычно при приложении к телу внешних сил сначала наблюдается упругая деформация, а затем, по мере роста этих сил, она может перейти в пластическую.
Твердые тела сопротивляются внешним воздействиям. Это связано с тем, что частицы (атомы, ионы, молекулы), из которых тела построены, взаимодействуют между собой. Устойчивая структура твердого тела объясняется действием как сил притяжения, препятствующих удалению частиц друг от друга, так и сил отталкивания, не позволяющих частицам слиться друг с другом. Природа этих сил может быть разной, но в ее основе лежит электромагнитное взаимодействие - взаимодействие электрических и магнитных полей, образованных заряженными частицами (ионами, электронами, ядрами атомов).
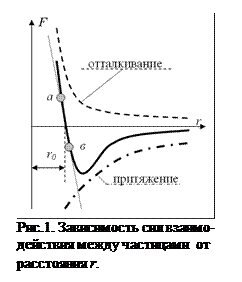
На рис. 1 между кривыми притяжения и отталкивания показана результирующая сила 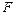 взаимодействия частиц. Расстояние
взаимодействия частиц. Расстояние 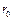 отвечает равенству сил притяжения и сил отталкивания. Обычно на таком расстоянии располагаются друг от друга частицы в твердых телах. Независимо от природы сил, характер зависимости их от расстояния между частицами сохраняется одинаковым (рис. 1). На относительно больших расстояниях (r > ro) преобладают силы притяжения, быстро увеличивающиеся с уменьшением расстояния; при малых расстояниях (r < ro) преобладают силы отталкивания, тоже увеличивающиеся с уменьшением расстояния, но значительно быстрее, чем силы притяжения. В результате приложения к телу растягивающих сил частицы раздвигаются, силы притяжения становятся больше сил отталкивания. Они и возвращают частицы в положение равновесия ( r = ro) после прекращения действия внешних сил. Сжимающие внешние силы делают расстояние между частицами меньше равновесного, при этом силы отталкивания превосходят по величине силы притяжения, и возвращают частицы в положение равновесия после снятия нагрузки.
отвечает равенству сил притяжения и сил отталкивания. Обычно на таком расстоянии располагаются друг от друга частицы в твердых телах. Независимо от природы сил, характер зависимости их от расстояния между частицами сохраняется одинаковым (рис. 1). На относительно больших расстояниях (r > ro) преобладают силы притяжения, быстро увеличивающиеся с уменьшением расстояния; при малых расстояниях (r < ro) преобладают силы отталкивания, тоже увеличивающиеся с уменьшением расстояния, но значительно быстрее, чем силы притяжения. В результате приложения к телу растягивающих сил частицы раздвигаются, силы притяжения становятся больше сил отталкивания. Они и возвращают частицы в положение равновесия ( r = ro) после прекращения действия внешних сил. Сжимающие внешние силы делают расстояние между частицами меньше равновесного, при этом силы отталкивания превосходят по величине силы притяжения, и возвращают частицы в положение равновесия после снятия нагрузки.
Зависимость результирующей силы взаимодействия между частицами от расстояния имеет сложный вид, но при небольших деформациях (участок  на рис.1) эта зависимость близка к линейной. Здесь величина силы пропорциональна расстоянию между частицами. Поэтому при малых деформациях справедлив закон Гука:
на рис.1) эта зависимость близка к линейной. Здесь величина силы пропорциональна расстоянию между частицами. Поэтому при малых деформациях справедлив закон Гука:
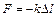 , ,
| (1) |
где 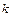 - коэффициент упругости, зависящий от природы твердого тела и его размеров, Δl - абсолютное изменение длины стержня. Знак минус указывает на то, что сила всегда направлена к положению равновесия (противоположно направлению деформаций). При приложении внешних сил
- коэффициент упругости, зависящий от природы твердого тела и его размеров, Δl - абсолютное изменение длины стержня. Знак минус указывает на то, что сила всегда направлена к положению равновесия (противоположно направлению деформаций). При приложении внешних сил  внутренние силы
внутренние силы  равны им по величине и направлены в противоположную сторону.
равны им по величине и направлены в противоположную сторону.
Для исключения влияния размеров тела в закон Гука вводят понятия
относительной деформации 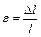 , ,
| (2) |
и нормального напряжения 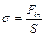 , ,
| (3) |
где 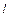 - исходный размер тела в направлении деформации;
- исходный размер тела в направлении деформации;
 - площадь поперечного сечения деформируемого тела.
- площадь поперечного сечения деформируемого тела.
Тогда выражение (1) запишется так:
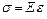 . .
| (4) |
где 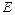 - модуль упругости.
- модуль упругости.
Следовательно, нормальные напряжения в деформируемом теле пропорциональны его относительной деформации.
Модуль упругости зависит только от природы частиц, образующих тело, и от их взаимного расположения. Эта важнейшая упругая характеристика весьма мало чувствительна к изменению состава (примеси) или внутренней структуры твердого тела (термическая обработка). Для монокристаллических твердых тел модуль упругости зависит от направления.
3.2. Измерение модуля упругости с помощью магнитострикции
Методом магнитострикции возбуждают в металлическом стержне упругие колебания, они распространяются в виде продольных волн вдоль стержня, доходят до его концов, отражаются и идут в обратном направлении. Отраженные волны интерферируют с прямыми и образуют стоячую волну. Скорость распространения таких волн в твердых телах связана с модулем упругости тела. Определяя эту скорость по резонансной частоте колебаний, возможно рассчитать модуль упругости.
Скорость распространения упругих продольных волн υ в твердых телах определяется выражением
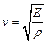 , ,
| (5) |
где 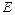 - модуль упругости;
- модуль упругости; 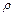 - плотность тела.
- плотность тела.
С другой стороны, длина волны λ связана со скоростью ее распространения уравнением
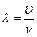 . .
| (6) |
Здесь  - частота колебаний.
- частота колебаний.
Совместное решение уравнений (5) и (6) приводит к выражению
 . .
| (7) |
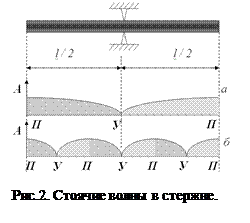 Если стержень закрепить посередине и возбудить в нем чередованием деформаций растяжения и сжатия продольные (направленные вдоль стержня) упругие колебания, то в таком стержне установятся стоячие волны (рис. 2) как результат интерференции прямой и отраженной от конца стержня волн. Для стоячей волны характерна различная амплитуда колебаний частиц (в зависимости от их расположения). Точки с амплитудой, равной нулю, называют узлами (У), а с максимальной амплитудой - пучностями (П). Обычно в точках закрепления образуются узлы, а на свободных концах - пучности.
Если стержень закрепить посередине и возбудить в нем чередованием деформаций растяжения и сжатия продольные (направленные вдоль стержня) упругие колебания, то в таком стержне установятся стоячие волны (рис. 2) как результат интерференции прямой и отраженной от конца стержня волн. Для стоячей волны характерна различная амплитуда колебаний частиц (в зависимости от их расположения). Точки с амплитудой, равной нулю, называют узлами (У), а с максимальной амплитудой - пучностями (П). Обычно в точках закрепления образуются узлы, а на свободных концах - пучности.
Так как в стоячих волнах расстояние между узлом и пучностью равно четверти длины волны (λ/4), то в простейшем случае, (рис. 2, а) в колеблющемся стержне образуется один узел (посередине) и две пучности (на концах). На рис. 2 по вертикали отложена амплитуда колебаний A. В другом случае могут образоваться три узла и четыре пучности (рис.2, б) либо пять узлов и шесть пучностей и т.д.
Обобщая, можно сказать, что по длине стержня 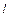 должно укладываться нечетное число полуволн:
должно укладываться нечетное число полуволн:
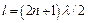
| (8) |
где 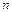 - целое число, принимающее значения
- целое число, принимающее значения 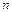 = 0,1,2,3..., т.е. в стержне могут возникать стоячие волны с длиной, удовлетворяющей условию (8).
= 0,1,2,3..., т.е. в стержне могут возникать стоячие волны с длиной, удовлетворяющей условию (8).
С учетом условия (6) выражение (7) перепишется в виде:
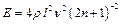 (9)
(9)
При 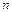 = 0 говорят об основном тоне колебаний, при
= 0 говорят об основном тоне колебаний, при 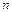 = 1,2,3,4...- об обертонах колебаний. В данной работе определяют основной тон (
= 1,2,3,4...- об обертонах колебаний. В данной работе определяют основной тон ( 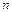 = 0). Выражение для расчета модуля упругости запишется так:
= 0). Выражение для расчета модуля упругости запишется так:
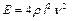
| (10) |
Колебания в стержне возбуждаются методом магнитострикции. Это явление состоит в изменении размеров тела в направлении намагничивания (тела в магнитном поле могут как сжиматься, так и удлиняться). Количественно магнитострикция характеризуется относительным удлинением тела ( 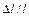 ) в магнитном поле. Оно невелико и колеблется в пределах
) в магнитном поле. Оно невелико и колеблется в пределах 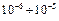 . Свойством магнитострикции обладают все тела, но у ферромагнетиков оно выражено более заметно.
. Свойством магнитострикции обладают все тела, но у ферромагнетиков оно выражено более заметно.
Магнитострикция связана с изменением сил взаимодействия между частицами твердого тела при помещении его во внешнее магнитное поле (меняется расстояние между частицами, отвечающее равенству сил притяжения и отталкивания). Для возбуждения колебаний в стержне его помещают в переменное магнитное поле катушки, питаемой переменным током звуковой или ультразвуковой частоты. Так как магнитострикция является четным эффектом (не чувствительным к перемене поля на обратное), то колебания имеют удвоенную частоту по сравнению с частотой переменного тока. Но если на переменное магнитное поле наложить постоянное (чтобы напряженность результирующего поля не меняла знака), то частоты магнитострикционных колебаний и переменного тока будут совпадать. Такое поле создается дополнительной катушкой (подмагничивающей).
Колебания, возбуждаемые в стержне магнитострикционным методом, будут вынужденными. Как известно, для вынужденных колебаний характерно явление механического резонанса, когда амплитуда колебаний резко возрастает. Это явление имеет место, когда частота вынужденных колебаний оказывается весьма близкой к частоте собственных колебаний, которая удовлетворяет условию (8). Резонансную частоту определяют по резкому увеличению амплитуды колебаний, которая входит в выражение (10) для определения модуля упругости.
4. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ИЗМЕРЕНИЯ
На рис. 3 приведена принципиальная схема установки для определения модуля упругости. Исследуемый стержень 1 закрепляется посередине зажимом 2. На стержень надеты две катушки: катушка 3, создающая переменное магнитное поле в стержне и питаемая переменным током звуковой частоты от генератора звуковых сигналов 4, и катушка 5, создающая подмагничивающее поле, и питаемая от источника постоянного тока 6. Возникающие в стержне продольные механические колебания воспринимаются динамическим микрофоном 7, слегка прижатым к одному из концов стержня, и превращаются в электромагнитные колебания. Электромагнитные колебания поступают на вертикально отклоняющие пластины осциллографа 8. На горизонтально отклоняющие пластины с помощью задающего генератора осциллографа подается переменный сигнал, заставляющий электронный луч на экране описывать горизонтальную линию. Переменный сигнал, подаваемый на вертикально отклоняющие пластины, заставляет луч рисовать на экране синусоиду.
 Меняя (с помощью регулятора частоты) частоту переменного магнитного поля, достигают выполнения условия механического резонанса. Он фиксируется по скачкообразному возрастанию амплитуды колебаний (увеличение отклонения луча по вертикали). Резонансная частота входит в расчетную формулу (10). Согласно (9) таких резонансных частот будет несколько (
Меняя (с помощью регулятора частоты) частоту переменного магнитного поля, достигают выполнения условия механического резонанса. Он фиксируется по скачкообразному возрастанию амплитуды колебаний (увеличение отклонения луча по вертикали). Резонансная частота входит в расчетную формулу (10). Согласно (9) таких резонансных частот будет несколько ( 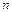 = 0,1,2,3...). Необходимо определить частоту основного тона (
= 0,1,2,3...). Необходимо определить частоту основного тона ( 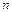 = 0). Это несложно сделать, потому что она отвечает наибольшей амплитуде; у обертонов (
= 0). Это несложно сделать, потому что она отвечает наибольшей амплитуде; у обертонов ( 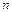 = 1,2,3...) резонансные амплитуды будут значительно меньше по величине.
= 1,2,3...) резонансные амплитуды будут значительно меньше по величине.
5. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ОБРАБОТКИ РЕЗУЛЬТАТОВ
Приборы и принадлежности: установка для определения модуля упругости, три стальных стержня разной длины, генератор звуковых сигналов, осциллограф.
Расчетная формула
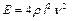
|
где 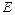 - модуль упругости;
- модуль упругости; 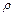 - плотность стержня;
- плотность стержня; 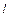 - длина стержня;
- длина стержня;  - резонансная частота (основной тон).
- резонансная частота (основной тон).
1) Соберите электрическую цепь, не замыкая подмагничивающую обмотку (ключ "К" разомкнут).
2) Проверьте начальное положение переключателей на звуковом генераторе 4 и осциллографе 8 согласно настольному руководству (см. рис. 3).
3) Запишите в табл. 5.1 средние значения длин ‹l› стержней, приведенные на установке. Рядом запишите среднеквадратичные ошибки для длин. При отсутствии этих данных выполните измерение длин. Запишите значение средней плотности ‹ρ› стали.
4) Поместите один из исследуемых стержней в установку так, чтобы его конец был слегка прижат к динамическому микрофону. Закрепите стержень в середине зажимом 2.
5) Включите звуковой генератор и осциллограф в сеть на 220 В и поставьте тумблеры "сеть" в положение "включение". Дайте прогреться приборам 3 мин.
6) Регуляторами осциллографа "яркость" и "фокус" добейтесь появления резкого электронного луча на экране электронно-лучевой трубки. Луч при этом рисует горизонтальную линию. Выведите эту линию на середину трубки с помощью регуляторов "ось-Х" и "ось-У".
7) Подайте на катушку 3, создающую переменное магнитное поле, напряжение 50 В с помощью переключателя звукового генератора "регулятор выхода". В дальнейшем при всех измерениях следите за постоянством этого напряжения.
8) Включите подмагничивающую обмотку (замкните ключ "К").
9) Регулятором звукового генератора "частота", плавно увеличивая частоту от 2000 до 20000 Гц, пройдите весь диапазон частот. При этом внимательно следите за электронным лучом на экране осциллографа. Луч описывает синусоиды. Амплитуда отклонений луча по вертикали будет меняться: от почти незаметной до заметной. Определите резонансную частоту основного тона. Она характеризуется резким наибольшим отклонением электронного луча по вертикали. Запишите в табл. 5.2 значение резонансной частоты.
10) Сдвиньте регулятор "частота" и снова подведите его в положение, соответствующее максимальной амплитуде. Запишите значение резонансной частоты. Таких измерений сделайте три для каждого стержня.
11) Поочередно замените исследованный стержень другими и повторите все измерения по пп. 7-10 для них, записывая частоты в таблицу 1.
Таблица 1. Результаты измерений и вычислений
‹ρ› =
| Стержень 1 | Стержень 2 | Стержень 3 | ||||
| ‹l1› = | ‹l2› = | ‹l3› = | ||||
| νi, Гц | Ei, Па | νi, Гц | Ei, Па | νi, Гц | Ei, Па | |
| среднее |
12) Тумблеры "сеть" на приборах поставьте в положение "выключено", отсоедините их от источника питания. Разомкните (ключом "К") подмагничивающую обмотку.
13) Рассчитайте средние значения модулей упругости для каждого из стержней. Перенесите их средние значения в таблицу 2.
Таблица 2.
| Еі, Па | Еі-‹E› | (Еі- ‹E›)2 | |
| Σ |
14) Определите выборочное среднее модуля упругости стали по данным таблицы 2. Задавшись доверительной вероятностью Рα рассчитайте доверительный интервал (как для прямых измерений).
Результат должен быть записан в виде Е=‹E› ±∆Е с указанием доверительной вероятности Рα.
| <== предыдущая лекция | | | следующая лекция ==> |
| ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ОБРАБОТКИ РЕЗУЛЬТАТОВ | | | Международные обозначения критических температур на диаграмме железо-углерод |
Дата добавления: 2015-04-25; просмотров: 1247;
