Математическая модель условий окупаемости затрат на повышение теплозащиты ограждающих конструкций зданий

Математическая модель, предложенная В.Г Гагариным, за базовый (нулевой) вариант с минимальным допустимым сопротивлением теплопередаче R₀⁰ принимает вариант ограждающей конструкции с сопротивлением теплопередаче, не превышающим санитарно-гигиенические требования. При применении других вариантов повышения теплозащиты здания минимизируется разность приведенных затрат DП на их устройство относительно базового варианта:

DП = (К₁ – К₀) – Т (Э₀ – Э₁) =DК – Т DЭ (5.2)

При этом DК представляет собой единовременные затраты на дополнительное утепление конструкции, а DЭ – экономию средств на отопление, обусловленную дополнительным утеплением. Если ограждающая конструкция обладает достаточной долговечностью, то дополнительные единовременные затраты окупаются при значении Т₀, определяемом из условия DП = 0 формулой:

Т₀ = DК / DЭ (5.3)

Величина Т₀ представляет собой период окупаемости. В рамках рассмотренной модели, при отсутствии платы за кредит банка, единовременные затраты на дополнительное утепление обязательно окупятся, хотя, возможно, и в течение довольно длительного срока (рис. 5.2).

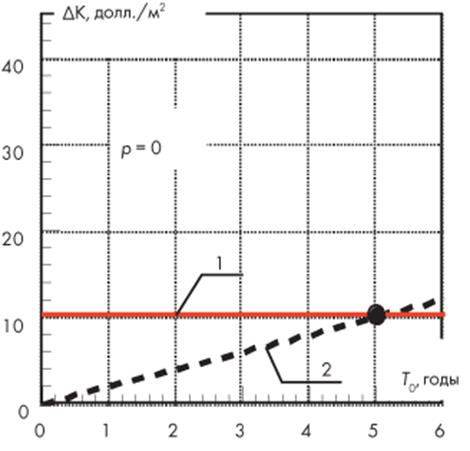
Рисунок 5.2 – Период окупаемости Т₀ единовременных затрат DК на дополнительное утепление ограждающей конструкции при отсутствии процентной ставки за банковский кредит:

1 – изменение во времени долга за кредит банка на единовременные затраты;
2 – прибыль, получаемая от экономии энергии на отопление при эксплуатации ограждающей конструкции

Иная ситуация получается, если учитывать платежи за кредит банка (процентную ставку) по затратам на дополнительное утепление ограждающей конструкции. В этом случае можно приводить затраты будущих лет к начальному периоду времени (метод дисконтирования) или приводить единовременные затраты и эксплуатационные расходы к некоторому моменту времени в будущем (метод компаудинга) [6]. Оба метода дают одинаковый результат. Опыт показывает, что применение соответствующих формул, хорошо известных в экономике, является непонятным для инженеров, вследствие чего остаются непонятными и последующие выводы. Поэтому вывод всех уравнений, приведенных ниже, выполнен «с нуля», при этом результат получен тот же, что и при использовании указанных формул [6]. При дальнейшем рассмотрении предполагается:

1. Процентная ставка при заимствовании равна процентной ставке при инвестировании;

2. Лимит при получении кредита отсутствует;

3. Процентная ставка одинакова на всех субпериодах рассматриваемого периода в Т лет.

Совокупность таких условий в теории инвестиционных расчетов называется «Совершенный неограниченный рынок капитала при пологой кривой процента» [7]. Можно усложнять эти условия с целью приближения их к реальности, например, учитывать изменение процентной ставки, но это усложнит схему рассуждений и вряд ли добавит точности. Кроме этих предположений в качестве денежной единицы принимается доллар США. Это сделано только для возможности проведения международных сопоставлений. При необходимости можно заменить доллар национальной валютой. Как принято в западных странах, домовладелец для дополнительного утепления 1 м² ограждающей конструкции своего дома берет кредит в банке в сумме DК, долл./м², с фиксированной годовой процентной ставкой за кредит р, % в год. Для упрощения выкладок величину p используется в долях единицы. Каждый год долг домовладельца увеличивается в (1 + p) раз. Через Т лет долг домовладельца банку составит:

DК (1 + р)^Т (5.4)

Однако за счет дополнительного утепления ограждающей конструкции снизятся теплопотери через нее, и, следовательно, домовладелец будет получать ежегодную прибыль за счет снижения стоимости отопления. На 1 м² ограждения в год это составит DЭ долл./(м²•год). Полученную прибыль домовладелец возвращает банку в начале следующего года, то есть уменьшает кредит на величину DЭ. Это равносильно тому, что домовладелец делает «накопительный вклад» в банк в сумме DЭ с той же фиксированной годовой процентной ставкой р % в год. Такую операцию домовладелец проводит ежегодно. Если утепление здания было выполнено в тот же год, когда был взят кредит в банке, то через год домовладелец уже начнет делать свои вклады. Его первый вклад будет увеличиваться ежегодно в (1 + p) раз и через T лет после взятия кредита будет равен DЭ (1 + р)^Т-1. Вклад, сделанный на второй год в это же время, станет равным DЭ (1 + р)^Т-2. Через Т лет весь «накопительный вклад» будет равен:

DЭ (1 + р)^Т-1 + DЭ (1 + р)^Т-2 +…+ DЭ = (DЭ (1 + р)^Т – DЭ) / р =

= DЭ ((1 + р)^Т – 1) / р (5.5)

При суммировании в (5.5) применена формула суммы геометрической прогрессии. С учетом (5.4) и (5.5) разность DП составит:

DП = DК (1 + р)^Т – DЭ ((1 + р)^Т – 1) / р) (5.6)

Дополнительные единовременные затраты DК окупаются при значении, Т₀, определяемом из условия DП = 0, то есть:

DK (1+p)^To = DЭ ((1+p)^To – 1) / p (5.7)

Решение этого уравнения относительно Т₀ дает:

Т₀ = ln[1 / (1 – (DК / DЭ) р)] / ln(1+ р) (5.8)

При р → 0 уравнение (5.8) переходит в (5.3). При р, отличном от 0, решение (5.8) существует только в том случае, если выражение под логарифмом положительно:

1 – (DК / DЭ) р > 0 (5.9)

Следовательно, единовременные затраты окупаются при условии:

DK / DЭ < 1 / p (5.10)

Выполнение этого неравенства является условием окупаемости любого мероприятия при ненулевой учетной ставке банка, то есть при существовании платы за кредит. Рыночная экономика западноевропейского образца как раз и характеризуется существенной платой за кредиты банков. Величина p иногда называется ростовщический процент. В русском языке такая плата, по сути являющаяся учетной ставкой за кредит банка, называлась лИхва, отсюда выражение «окупиться с лихвой», а ростовщик (банкир) назывался лихоимщик. Из (11.0) следует, что чем больше величина p, тем больше должна быть ежегодная прибыль DЭ от вложения средств DК, чтобы эти вложения окупились. При больших значениях p никакие долгосрочные инвестиции экономически невыгодны и могут осуществляться только на внеэкономической основе, то есть за счет бюджетных средств государства.

При решении теплофизической задачи теплопотери через 1 м² конструкции за отопительный период можно определить по формуле:

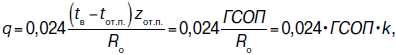(5.11)

где R₀ – сопротивление теплопередаче ограждающей конструкции, м²•°C/Вт;

k – коэффициент теплопередачи ограждающей конструкции, Вт/(м²•°C);

ГСОП – градусо-сутки отопительного периода, °C•сут./год, определяемые по формуле: ГСОП = (t_в – t_от.п.)z_от.п., t_в – температура внутреннего воздуха помещения, °С; t_от.п. – средняя температура отопительного периода, °С; z_от.п. – продолжительность отопительного периода, сут./год;

0,024 = 24 / 1 000 – переводной коэффициент, кВт•ч/ (Вт •сутки).

С учетом (1.11) годовая прибыль домовладельца за счет снижения теплопотерь через 1 м² ограждения определяется по формуле:

DЭ = (1/R₀⁰ –1/R₀¹)ГСОП•0,024•C_Т = –(k₁–k₀)×ГСОП•0,024•C_Т =

= –Dk•ГСОП•0,024×C_Т, (5.12)

где DЭ – годовая прибыль домовладельца за счет снижения теплопотерь через 1 м² ограждения при дополнительном утеплении, долл./(м²•год);

R₀⁰, R₀¹– сопротивления теплопередаче базового и рассматриваемого варианта ограждения, соответственно, м²•°C/Вт;

k₀, k₁ – коэффициенты теплопередачи базового и рассматриваемого варианта ограждения, соответственно, Вт/(м²•°C);

C_Т – стоимость тепловой энергии, долл./(кВт•ч).

С учетом (1.12) неравенство (1.10) принимает вид:

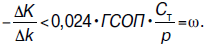(5.13)

Левая часть этого неравенства, (–DК / Dk), представляет собой удельные единовременные затраты на снижение коэффициента теплопередачи ограждающей конструкции на 1 Вт/(м²•°С) и определяется свойствами конструкции: стоимостью ее изготовления, стоимостью материалов, начальным значением k₀ и т. д. Правая часть, ω, напротив, никак не зависит от конструкции, а полностью определяется климатическими, географическими и экономическими характеристиками страны или региона. И эта правая часть представляет собой предельное значение для удельных единовременных затрат, при которых они окупаются. Если неравенство (1.13) не выполняется, то затраты на повышение сопротивления теплопередаче ограждающей конструкции никогда не окупятся (рис. 5.3), если выполняется – то окупятся (рис.5. 4).

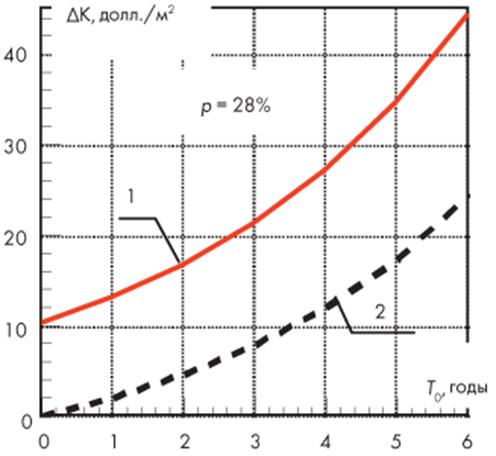
Рисунок 5.3- При наличии процентной ставки за банковский кредит и достаточно больших единовременных затратах на дополнительное утепление ограждающей конструкции эти затраты никогда не окупятся за счет прибыли, получаемой от экономии энергии на отопление, неравенство (5.13) не выполняется

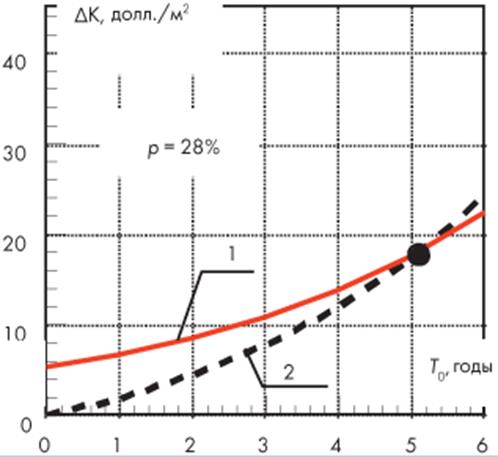
Рисунок 5.4 - При той же процентной ставке за банковский кредит, но меньших единовременных затратах на дополнительное утепление ограждающей конструкции, эти затраты могут окупиться за счет прибыли, получаемой от экономии энергии на отопление, неравенство (1.13) выполняется

Интересно рассмотреть другие варианты записи неравенства (5.13).

DK • p < 0,024 ГСОП (–Dk)C_т. (5.13а)

Левая часть неравенства (5.13а) представляет собой денежную сумму, которую необходимо ежегодно платить банку за кредит. Правая часть представляет собой денежную сумму, которая ежегодно образуется за счет экономии тепловой энергии вследствие снижения теплопотерь через ограждающую конструкцию с дополнительным утеплением. Следовательно, смысл неравенства (13а) заключается в том, что ежегодная экономия денежных средств должна превышать ежегодную плату за кредит банка. Только в этом случае возможна окупаемость средств на повышение теплозащиты ограждающей конструкции. Еще одна форма записи неравенства (5.13):

pDK/С_т < 0,024 ГСОП(–Dk) (5.13б)

Здесь DK/C_т – стоимость в энергетических единицах (кВт•ч/м²) единовременных затрат на утепление одного м² ограждающей конструкции. Левая часть неравенства (13б) pDK/C_т представляет собой ежегодную плату банку за кредит в энергетических единицах (кВт•ч/(м²∙год)). Правая часть неравенства 0,024•ГСОП(–Dk) представляет собой ежегодную экономию тепловой энергии за счет снижения теплопотерь через 1 м² ограждающей конструкции, кВт•ч/(м² • год). Смысл неравенства (5.13б) заключается в том, что ежегодная экономия энергии должна превышать ежегодные процентные отчисления банку за кредит на единовременные затраты, выраженные в энергетических единицах. То есть если вместо денег все оценивать в единицах энергии, то в качестве условия окупаемости вложений следует использовать неравенство (5.13б). Неравенства (5.13), (5.13а) и (5.13б) можно представить в безразмерном виде, получающемся из (13) (при этом следует помнить, что p измеряется в долях ед./год):

DK•p / (C_т(–Dk)ГСОП•0,024) < 1 (5.13в)

Левая часть (5.13в) является безразмерным критериальным числом, его можно использовать для оценки окупаемости инвестиций в утепление зданий. Неравенства (5.13а) – (513в) эквивалентны (5.13). Любое из этих неравенств является критерием окупаемости затрат на повышение теплозащиты ограждающей конструкции. Однако неравенство (5.13) представляется более удобным для использования при решении практических задач. Его можно использовать непосредственно для анализа конкретных вариантов утепления ограждающей конструкции, а также при сопоставлении условий и периода окупаемости повышения теплозащиты зданий в различных странах. Во второй части статьи будет рассмотрено применение изложенной теории для решения ряда задач экономического анализа повышения теплозащиты зданий.