Операции над событиями
Раздел: Основы теории вероятностей
Тема: Случайные события. Классическое определение вероятности
План
1 Основные понятия.
2 Операции над событиями.
3 Теорема сложения вероятностей.
4 Условная вероятность.
5 Теорема умножения вероятностей.
Основные понятия
Определение. Событиемназывается всякий факт, который может произойти или не произойти в результате опыта.
При этом тот или иной результат опыта может быть получен с различной степенью возможности. Т.е. в некоторых случаях можно сказать, что одно событие произойдет практически наверняка, другое практически никогда.
В отношении друг друга события также имеют особенности, т.е. в одном случае событие А может произойти совместно с событием В, в другом – нет.
Определение. События называются несовместными, если появление одного из них исключает появление других.
Классическим примером несовместных событий является результат подбрасывания монеты – выпадение лицевой стороны монеты исключает выпадение обратной стороны (в одном и том же опыте).
Определение. Полной группой событий называется совокупность всех возможных результатов опыта.
Определение. Достоверным событиемназывается событие, которое наверняка произойдет в результате опыта. Событие называется невозможным, если оно никогда не произойдет в результате опыта.
Например, если из коробки, содержащей только красные и зеленые шары, наугад вынимают один шар, то появление среди вынутых шаров белого – невозможное событие. Появление красного и появление зеленого шаров образуют полную группу событий.
Определение. События называются равновозможными, если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью.
В приведенном выше примере появление красного и зеленого шаров – равновозможные события, если в коробке находится одинаковое количество красных и зеленых шаров.
Если же в коробке красных шаров больше, чем зеленых, то появление зеленого шара – событие менее вероятное, чем появление красного.
Определение. Вероятностью события А называется математическая оценка возможности появления этого события в результате опыта. Вероятность события А равна отношению числа, благоприятствующих событию А исходов опыта к общему числу попарно несовместных исходов опыта, образующих полную группу событий.
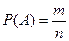
Исход опыта является благоприятствующим событию А, если появление в результате опыта этого исхода влечет за собой появление события А.
Очевидно, что вероятность достоверного события равна единице, а вероятность невозможного – равна нулю. Таким образом, значение вероятности любого события – есть положительное число, заключенное между нулем и единицей.

Пример. В коробке находится 10 шаров. 3 из них красные, 2 – зеленые, остальные белые. Найти вероятность того, что вынутый наугад шар будет красным, зеленым или белым.
Появление красного, зеленого и белого шаров составляют полную группу событий. Обозначим появление красного шара – событие А, появление зеленого – событие В, появление белого – событие С.
Тогда в соответствием с записанными выше формулами получаем:
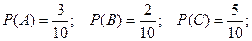
Отметим, что вероятность наступления одного из двух попарно несовместных событий равна сумме вероятностей этих событий.
Определение. Относительной частотой события А называется отношение числа опытов, в результате которых произошло событие А к общему числу опытов.
Отличие относительной частоты от вероятности заключается в том, что вероятность вычисляется без непосредственного произведения опытов, а относительная частота – после опыта.
Так в рассмотренном выше примере, если из коробки наугад извлечено 5 шаров и 2 из них оказались красными, то относительная частота появления красного шара равна: 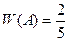
Как видно, эта величина не совпадает с найденной вероятностью.
При достаточно большом числе произведенных опытов относительная частота изменяется мало, колеблясь около одного числа. Это число может быть принято за вероятность события.
Классическое определение вероятности неприменимо к испытаниям с бесконечным числом исходов. Чтобы преодолеть этот недостаток вводится понятие геометрической вероятности, т.е. вероятности попадания точки в какой – либо отрезок или часть плоскости (пространства).
Так если на отрезке длиной L выделен отрезок длины l, то вероятность попадания наугад взятой точки в отрезок l равна отношению l/L.
Операции над событиями
Определение. События А и В называются равными, если осуществление события А влечет за собой осуществление события В и наоборот.
Определение. Объединениемили суммой событий Аk называется событие A, которое означает появление хотя бы одногоиз событий Аk.
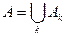
Определение. Пересечениемили произведениемсобытий Ak называется событие А, которое заключается в осуществлении всех событий Ak.

Определение. Разностью событий А и В называется событие С, которое означает, что происходит событие А, но не происходит событие В.
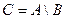
Дата добавления: 2015-04-21; просмотров: 1101;
