ЭНЕРГЕТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ТЕРМОДИНАМИЧЕСКИХ СИСТЕМ 4 страница

- установить количественную связь между размерами деталей машин;

- уточнить номинальные значения и допуски взаимосвязанных размеров;

- добиться наиболее правильной простановки размеров на чертежах;

- определить наиболее рентабельный вид взаимозаменяемости;

- определить операционные (промежуточные) размеры.

Основное уравнение размерной цепи.

Для проведения размерного анализа кроме размерной схемы необходимо составить уравнение размерной цепи, вытекающее из условия замкнутости: Если в размерную цепь входит m увеличивающих звеньев и n уменьшающих звеньев, то уравнение линейной размерной цепи имеет вид:

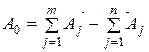(1)

Прямая и обратная задачи.

При расчете размерных цепей могут решаться две задачи:

1. Определение допуска и предельных отклонений составляющих размеров по заданным номинальным размерам всех звеньев цепи и заданным предельным размерам исходного (замыкающего) звена. (Прямая задача или проектный расчет).

2. Определение номинального размера и допуска замыкающего звена по заданным номинальным размерам и предельным отклонениям составляющих звеньев. (Обратная задача или проверочный расчет).

Методы достижения заданной точности исходного звена.

Существуют следующие методы достижения заданной точности исходного звена (решения размерных цепей):

1. Метод полной взаимозаменяемости (максимума – минимума).

2. Теоретико-вероятностный метод.

3. Метод групповой взаимозаменяемости.

4. Метод регулирования.

5. Метод пригонки.

1. Метод полной взаимозаменяемости.

Характеристика.

Детали соединяются на сборке без дополнительных операций. Значения замыкающего звена не выходят за установленные пределы. Расчет размерной цепи производится методом максимума – минимума.

Преимущества.

Простота и экономичность сборки; упрощение организации поточного сборочного процесса; возможность широкого кооперирования.

Недостатки.

Допуски составляющих звеньев получаются наименьшими из всех методов, что может оказаться неэкономичным.

Область применения.

В индивидуальном и мелкосерийном производстве, при большей величине допуска на исходное звено и малом числе составляющих звеньев.

Выбор метода решения размерных цепей.

При выборе метода решения размерных цепей необходимо учитывать:

· Функциональное назначение изделия;

· Его конструктивные и технологические особенности;

· Стоимость изготовления и сборки;

· Эксплуатационные требования;

· Тип производства и другие факторы.

Заданная точность исходного звена должна достигаться с наименьшими технологическими и эксплуатационными затратами.

При прочих равных условиях рекомендуется в первую очередь выбирать такие методы решения размерных цепей, при которых сборка производиться без подбора, пригонки и регулирования, т.е. методы полной взаимозаменяемости и вероятностный.

Если применение этих методов экономически нецелесообразно или технически невозможно, следует перейти к использованию одного из методов неполной взаимозаменяемости.

При выборе метода расчета цепей можно ориентироваться на среднюю величину допуска составляющих звеньев или среднюю степень точности (квалитет) составляющих звеньев.

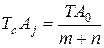(2)

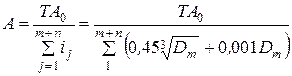(3)

Метод полной взаимозаменяемости.

После составления уравнения размерной цепи (1) и решения его относительно 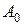можно определить предельные размеры замыкающего звена:

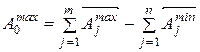(4)

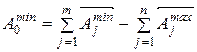(5)

Вычитая почленно из (4) выражение (5) получим формулу для определения допуска замыкающего звена:

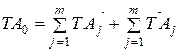(6)

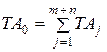(7)

Анализируя формулу (7) можно сделать следующие выводы:

1. В качестве замыкающего звена при сборке или изготовлении необходимо принимать наименее ответственный размер.

2. Точность замыкающего звена увеличивается с уменьшением допусков составляющих звеньев.

3. Сокращение числа звеньев приводит к повышению точности замыкающего звена; чем меньше число составляющих, тем больше допуски на составляющие звенья при той же величине допуска на исходное (замыкающее) звено, тем меньше стоимость изготовления.

Если из уравнений (4) и (5) вычесть последовательно уравнение (1), получим

выражения для определения предельных отклонений замыкающего (исходного) звена:

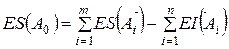(8)

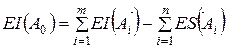(9)

При расчете размерных цепей часто оказывается удобным оперировать не предельными отклонениями ES и EI, а средними отклонениями Е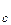

РИСУНОК.

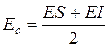(10)

Сложив почленно уравнения (8) и (9) и учитывая (10) получим среднее отклонение поля замыкающего звена.

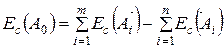(11)

Решение прямой задачи.

Такая задача встречается гораздо чаще. Она наиболее важна, поскольку конечная цель расчета допусков составляющих размеров при заданной точности сборки (заданном допуске исходного звена) – обеспечить выполнение машиной ее функционального назначения. Эту задачу можно решать одним из следующих способов.

Способ равных допусков.

Применяется, если составляющие размеры входят в один интервал размеров и могут быть выполнены с примерно одинаковой экономической точностью.

Допуски всех составляющих звеньев принимаются одинаковыми.

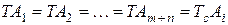(12)

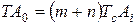
Используя уравнение (7) и равенство (12) получим выражение 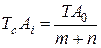(2):

(2)

Полученный средний допуск 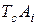корректируют для всех или некоторых составляющих звеньев в завасимости от их номинальных размеров, технологических возможностей изготовления, конструктивных требований. При этом должно выполняться условие:

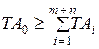(13)

При этом выбирают стандартные поля допусков желательно предпочтительного применения.

Способ равных допусков прост, но недостаточно точен, т.к. корректировка допусков произвольна. Его можно рекомендовать для предварительного назначения допусков составляющих размеров.

Способ допусков одного квалитета.

Применяется, если все составляющие размеры могут быть выполнены с допуском одного квалитета и допуски составляющих размеров зависят от их номинального значения.

Известны номинальные размеры всех звеньев и предельные отклонения исходного (замыкающего звена).

Требуемый квалитет определяют следующим образом:

Допуск составляющего размера: 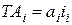, где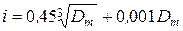

Используя формулу (7):

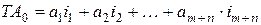
По условию 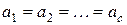. Тогда

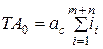
Откуда получаем формулу 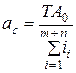(3):

(3)

По значению 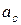выбирают ближайший квалитет. Найдя по таблицам ГОСТа 25347-82 допуски составляющих размеров, корректируют их значения. Допуски для охватывающих размеров рекомендуется определять как для основного отверстия, а для охватываемых – как для основного вала. При этом должно соблюдаться условие (13).

Найдя допуски 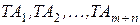по заданным отклонениям 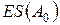и 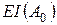определяют значения и знаки верхних и нижних отклонений составляющих размеров так, чтобы они удовлетворяли уравнениям (8) и (9).

Пример. Определить допуски составляющих размеров деталей сборочной единицы (см. рис.). Заданы номинальные значения составляющих размеров и предельные отклонения исходного звена: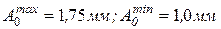

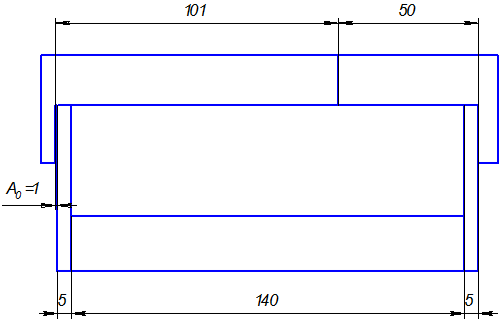
Рисунок 1 – Схема размерной цепи

Находим номинальный размер исходного звена по (1):

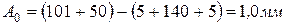
Наименьший предельный размер совпадает с номинальным, поэтому:

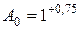и 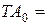0,75 мм.

Среднее число единиц допуска в размерной цепи определяем по (3)

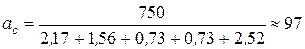
Для 10 квалитета а = 64

Для 11 квалитета а = 100

Устанавливаем для всех размеров цепи, кроме А₄, допуск по 11 квалитету. Допуск размера А₄ можно назначить несколько меньшим, т.к. вал по этому размеру легко обработать с высокой точностью.

По таблицам ГОСТ 25347-82 находим допуски на размеры А₁, А₂, А₃, А₅: 0,22; 0,16; 0,075; 0,075 мм; Т(А₄) = 0,25 мм; на долю размера А₄ остается допуск 0,22 мм:

ТА₄ = 0,75 – (0,22+0,16+0,075+0,075) = 0,22 мм.

Однако целесообразно принять его стандартным по 10 квалитету 0,16.

Назначаем предельные отклонения:

А₁ = 101^+0,22

А₂ = 50^+0,16

А₃ = А₅ = 5_-0,075

А₄ = 140_-0,16

Проверка:0,75 мм > 0,22+0,16+0,075+0,075+0,16 = 0,69 мм

Условие (13) выполняется.

2. Теоретико – вероятный метод.

Характеристика.

Детали соединяются на сборке, как правило, без пригонки, регулировки, подбора, при этом у небольшого (заранее принятого) количества изделий (обычно 3 изделия на 1000, процент риска 0,27) значения замыкающих звеньев могут выйти за установленные пределы. Расчет размерной цепи производится вероятностным методом.

Преимущества.

Те же, что и у метода полной взаимозаменяемости плюс экономичность изготовления деталей за счет расширенных полей допусков (по сравнению с предыдущим методом).

Недостатки.

Возможны, хотя и маловероятны, дополнительные затраты на замену или подгонку некоторых деталей.

Область применения.

В серийном и массовых производствах; при малом допуске исходного звена и большом числе составляющих звеньев.

Расчет размерных цепей теоретико – вероятностным методом.

Этот метод базируется на основных зависимостях метода максимума – минимума. Однако он учитывает более реальное распределение размеров в пределах поля допуска. В теории размерных цепей наиболее часто применяются следующие основные законы рассеивания размеров деталей: а) нормальный закон (закон Гаусса); б) закон треугольника (закон Симсона).

Уравнение (7) для определения допуска замыкающего (исходного) звена при расчете ТВМ принимает вид:

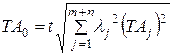(14)

где 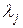- коэффициент относительного рассеивания, зависящий от закона рассеивания.

При расчетах коэффициент 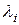принимают равным:

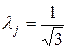
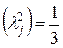, если ничего не известно о характере кривой рассеивания размеров деталей (мелкосерийное и индивидуальное производство);

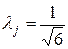
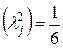, если предполагается, что рассеивание размеров деталей близко к закону треугольника;

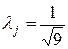
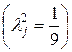, если кривая рассеивания имеет нормальный характер (крупносерийное и массовое производство)

t – коэффициент, зависящий от % риска Р, принимаемый по таблице.

Рассмотрим пример. Для линейной размерной цепи, состоящей из 5 звеньев:

По методу max – min: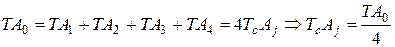

По методу ТВМ: 0,27%: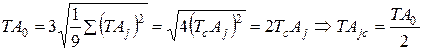

0,01%: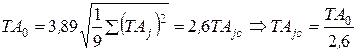

32%: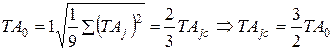

Таким образом для линейных цепей при нормальном законе распределения размеров деталей (Р = 0,27%)

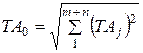(15)

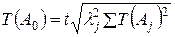
Способ равных допусков.

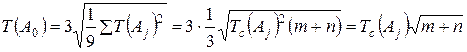
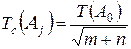(16)

Способ допусков одного квалитета.

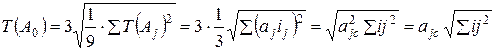
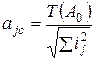(17)

Решим нашу задачу (см. рис. выше).

Пример.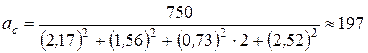

12 кв. а = 160

13 кв. а = 250

Таким образом ТВМ позволяет назначить более широкие допуски на составляющие звенья, чем метод max – min.

Лекция № 9 «Взаимозаменяемость, методы и средства измерения и контроля зубчатых передач»

В машиностроении наибольшее распространение получили понижающие зубчатые передачи: цилиндрические, конические, червячные, гипоидные. Встречаются передачи с внутренним и наружным зацеплением. Наибольшее распространение в промышленности получили эвольвентные зубчатые передачи с прямым и косым зубом.

ГОСТ 13755-81 устанавливает основные параметры зубчатых передач:

- шаг;

- модуль;

- число зубьев;

- делительный диаметр;

- ширина зубчатого венца;

- угол профиля зуба;

- угол наклона линии зуба;

- коэффициент смещения исходного контура;

- межосевое расстояние;

- гарантированный боковой зазор передачи.

Эксплуатационные требования к зубчатым передачам.

По служебному назначению зубчатые передачи условно делят на 4 группы:

- кинематические (отсчетные);

- скоростные;

- тихоходные силовые;

- общего назначения.

- К кинематическим передачам относятся зубчатые передачи измерительных инструментов, делительных механизмов металлорежущих станков, планетарные зубчатые передачи и т.д. Кроме этих передач имеют малый модуль и работают при малых нагрузках и скоростях. Основным эксплуатационным требованием к таким передачам является повышенная кинематическая точность, т.е. согласованность углов поворота ведущего и ведомого колес передачи.

К реверсивным кинематическим передачам предъявляются требования минимального гарантированного бокового зазора.

- Скоростные зубчатые передачи работают при скоростях свыше 5 м/с. К ним относятся з.п. редукторов паровых и газовых турбин, пробок скоростей, первых ступеней редукторов общего назначения. Скоростные передачи не требуют высокую кинематическую точность.

К ним предъявляются повышенные требования к плавности работы с тем, чтобы уменьшить шум и вибрации передач.

Для уменьшения габаритов передач предъявляются повышенные требования к контакту зубьев передачи.

Скоростные передачи работают при повышенных боковых зазорах, которые компенсируют нагрев передачи и исключают гидравлические удары.

- К силовым передачам относятся з.п. шестерных клетей прокатных станов, подъемно – транспортных механизмов, редукторов привода проходческих машин и т.п. Колеса имеют большой модуль. Основное точностное требование к ним – обеспечение более полного использования боковых поверхностей зубьев, т.е. получение наибольшего пятна контакта зубьев.

- К передачам общего назначения не предъявляется повышенные требования по точности

Системы точности зубчатых передач.

ГОСТ 1643 –91 устанавливает 12 степеней точности зубчатых колес в порядке убывания точности: 1, 2¼11, 12.

Для каждой степени точности установлены нормы:

а) кинематической точности;

б) плавности работы;

в) контакта зубьев.

Для з.п. с выраженными кинематическими свойствами (металлорежущий станок) назначается степень точности по нормам кинематической точности. Степень точности по нормам плавности назначают на 1 грубее, чем по кинематической точности.

5 – 6 – 6

Основным показателем точности скоростных з.п. и общего назначения является степень точности по нормам плавности, которую выбирают в зависимости от окружной скорости и типа передачи (прямозубая, косозубая …) и термообработки зубьев.

Если степень точности по нормам плавности выбрана точнее 8, то с целью снижения трудоемкости целесообразно степень точности по нормам кинематической точности принимать на 1-2 грубее, чем по плавности.

8 – 7 – 7

Независимо от показателей точности стандарт устанавливает 6 видов сопряжения по боковому зазору: A, B, C, D, E, H и 8 видов допусков на величину бокового зазора: x, y, z, a, b, c, d, h.

В горных машинах преимущественно применяется вид сопряжения В, реже А.

Выбирать вид сопряжения лучше всего по расчету

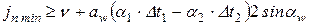
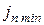- минимальный гарантированный боковой зазор.

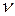- боковой зазор, необходимый для слоя смазки:

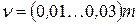
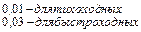
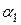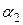; - коэффициент линейного теплового расширения материала передачи и корпуса.

а_w – межосевое расстояние.

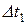- перегрев передачи

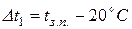
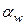- угол исходного контура ( )

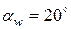Кинематическая точность.

Для обеспечения кинематической точности предусмотрены нормы, ограничивающие кинематическую погрешность передачи и колеса.

Кинематическая погрешность зубчатого колеса (F_{к п к}) определяется как разность между действительным и номинальным углами поворота зубчатого колеса, ведомого измерительным (образцовым) колесом. Она выражается в линейных величинах длиной дуги делительной окружности.

Показателем кинематической точности зубчатого колеса является наибольшая кинематическая погрешность зубчатого колеса (F^/_ir), которая равна наибольшей алгебраической разности значений кинематической погрешности зубчатого колеса за один полный оборот.

Контроль кинематической погрешности трудоемок, поэтому производится только при изготовлении особо точных колес (3…6 степени точности) с помощью кинематометров.

Составляющими кинематической погрешности являются:

а) накопленная погрешность окружного шага F_pr.

Допуск F_p.F_pr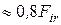

РИСУНОК.

б) радиальное биение зубчатого венца F_rr

Допуск F_r

Постоянной хордой называют отрезок прямой, соединяющий точки касания исходного контура с обоими профилями зуба в нормальном сечении.

в) колебание длины общей нормали F_VWr

Допуск F_VW Длина общей нормали W – это расстояние между двумя параллельными плоскостями, касательными к двум разноименным активным боковым поверхностям А и В зубьев колеса.

г) колебание измерительного межосевого расстояния за оборот колеса F_ir^¢¢ или на одном зубе f_ir^¢¢.

Допуски F_i^¢¢ и f_i^¢¢

Номинальным измерительным межосевым расстоянием а¢¢ называют расчетное расстояние между осями измерительного и рабочего колеса, имеющего наименьшее дополнительное смещение исходного контура.

Стандарт ГОСТ 1643 – 91 предусматривает контроль точности изготовления зубчатых колес по одному из комплексов:

1. Для передач 3¼6 степеней точности

- по кинематической погрешности F_ir^¢ (F_i^¢)

2. В условиях единичного производства:

- по накл. погреш. окружного шага F_pr (F_p);

- по радиальному биению зубчатого венца F_rr (F_r);

- по колебанию длин общей нормали F_vwr (F_vw).

3. В условиях крупносерийного производства

- по колебанию измерительного межосевого расстояния за оборот колеса F_ir^¢¢ (F_i^¢¢)

- по колебанию длины общей нормали F_vwr (F_vw).

Плавность работы.

Наиболее объективным показателем плавности работы зубчатых передач является местная кинематическая погрешность.

Местная кинематическая погрешность колеса f_ir^¢ - это наибольшая разность между местными соединениями (экстремальными) значениями кинематической погрешности зубчатого колеса.

Составляющими местной кинематической погрешности являются:

- отклонение шага f_ptr (допуск f_pt);

- отклонение шага зацепления f_pbr (f_pb);

- отклонение профиля зуба f_fr (f_f);

- колебание измерительного межосевого расстояния на одном зубе f_ir^¢¢ (f_i^¢¢).

Контакт зубьев.

Долговечность работы зубчатых передач зависит от полноты контакта сопряженных боковых поверхностей зубьев колес.

РИСУНОК.

h_cp – средняя высота следов прилегания зубьев.

h_c – высота зуба активной боковой поверхности.

Суммарным пятном контакта называют часть активной поверхности зуба колеса, на которой располагаются следы прилегания его к зубьям парного колеса после вращения собранной передачи при непрерывном контактировании зубьев обоих колес.

Суммарное пятно контакта оценивается по относительным размерам:

По длине зуба:

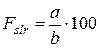(с < m)

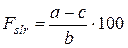(c > m)

по высоте:

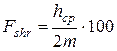
Показатели кинематической точности, плавности работы и контакта зависят от точности зубонарезного инструмента и не зависят от квалификации рабочего.

Боковой зазор зависит от правильности установки на станке межосевого расстояния «инструмент – заготовка», от режимов резания, т.е. от квалификации станочника.

Поэтому показатели бокового зазора контролируют на каждом колесе и допуски бокового зазора наносят на рабочий чертеж колеса.

Рассмотрим методы контроля бокового зазора.

Методы контроля бокового зазора.

Пассивные методы:

а) набором щупов;

б) индикатором часового типа;

в) по замерам толщины свинцовой пластинки, прокатанной между зубьями.

Активные методы:

а) контроль смещения исходного контура от его номинального положения (тангенциальные зубомеры);

б) контроль длины общей нормали (нормалемеры, штангенциркули);

в) контроль толщины зуба по постоянной хорде или по хорде делительной окружности (штангензубомеры);

г) контроль размера б.з. по роликам (рычажные скобы, оптиметры).

Контроль смещения исходного контура.

Для создания в зубчатой передаче гарантированного зазора производят уменьшение толщины зуба по сравнению с расчетной теоретической толщиной. Это уменьшение создается путем радиального смещения исходного контура рейки зубонарезного инструмента.

Дополнительное смещение исходного контура от его номинального положения в тело зубчатого колеса нормируется в ГОСТе 1643-81 двумя величинами:

- наименьшим дополнительным смещением исходного контура (E_HS);

- допуском на смещение исходного контура (Т_Н).

Наименьшее дополнительное смещение исходного контура (E_HS) назначают в

зависимости от степени точности по нормам плавности и вида сопряжения.

E_HS = f (m; z; степ. точн; вида сопр.)

Допуск на смещение исходного контура (Т_Н) установлен в зависимости от допуска на радиальное биение (F_r), вида сопряжения, причем Т_Н>F_r

T_H = f (m; z; степ. точн; вида сопр)

Контроль смещения исходного контура осуществляют с помощью тангенциального зубомера.

Контроль толщин зубьев по

постоянной хорде.

ГОСТ 1643-91 взамен измерения дополнительного смещения исходного контура разрешает производить измерение толщины зуба по постоянной хорде.

Постоянной хордой называют отрезок прямой, соединяющий точки касания исходного контура с обоими профилями зуба в нормальном сечении.

Номинальная величина толщины зуба

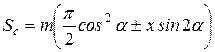
где х – коэффициент коррегирования

a - угол исходного контура.

Для коррегирования колес S_c = 1,387× m

Высота от окружности выступов до постоянной хорды

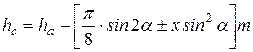
где h_a – высота головки зуба (для нормальных колес h_a = m)

Для коррегирования колес h_c = 0,7476×m

Предельные значения толщины зуба по постоянной хорде нормируют в ГОСТе: - наименьшим отлонением толщины зуба от номинальной (E_CS);

- допуском на толщину зуба (Т_с)

E_CS = f (вида сопряжения, степени точности по нормам плавности, делительного диаметра).

T_C = f (вида сопряжения, допуска на различное биение)

Контроль толщины зуба по постоянной хорде осуществляют с помощью штангензубомера.

(Показать прибор, рассказать о его устройстве).

Выполнение чертежей цилиндрических зубчатых колес.

Правила оформления нормируются ГОСТ 2.403-75.

На изображении зубчатого колеса указывают:

- Æ окружности выступов;

- ширину венца;

- шероховатость боковой поверхности зубьев;

- размеры фасок.

На чертеже помещают таблицу параметров.

Состоит из 3-х частей:

а) основные для изготовления;

б) для контроля;

в) справочные данные.

Модуль	m
Число зубьев	z
Угол наклонов зубьев	b	16°
Направление линии зуба	-	Левое
Исходный контур	-	ГОСТ 13755-81
Коэффициент смещения	Х
Степень точности по ГОСТ 1643-91		8 – В
Толщина зуба по постоянной хорде	Sc	9,71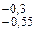
Высота до постоянной хорды	hC	S, 23
Делительный диаметр	d	436,93

Лекция №10 «Взаимозаменяемость резьбовых соединений»