Основное дифференциальное уравнение равновесия жидкости.

Жидкость будет находиться в состоянии равновесия, если каждый бесконечно малый ее элемент находится в равновесии под действием всей совокупности приложенных к этому элементу сил.

В неподвижной жидкости выбираем систему координат , в которой рассмотрим элементарный объем жидкости в виде параллелепипеда, грани которого параллельны координатным осям (рис.3.2)

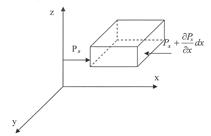
Рис. 3.2 Схема к выводу уравнения Эйлера

По принципу Даламбера тело находится в состоянии равновесия, если сумма проекций всех сил на координатные оси равнялась нулю:

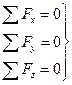(3.5)

В общем случае рассматриваемый нами элемент жидкости находится в равновесии под действием массовых и поверхностных сил. Величина массовых сил 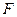пропорциональна массе жидкости 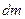, заключенной в рассматриваемом объеме 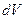. Масса жидкости с учетом ее плотности 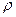определяется в виде:

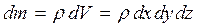(3.6)

где 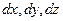- значения длин ребер прямоугольного параллелепипеда.

Поверхностные силы всегда направлены по нормалям к соответствующим граням рассматриваемого параллелепипеда. Давления, действующие вдоль ос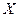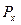и :

и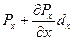

Составим уравнение равновесия сил вдоль оси :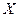

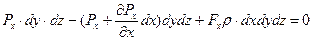(3.7)

Раскроем скобки и преобразуем.

Разделим все на 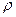, получаем выражение:

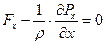
Аналогично на остальные оси.

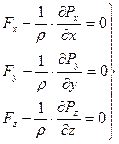(3.8)

Уравнение (3.8) называют дифференциальным уравнением идеальной, покоящейся жидкости в форме Эйлера.

Данное уравнение можно преобразовать, для чего умножим первое на 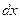, второе на 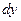, третье на .

Данные уравнения сложим и сгруппируем:

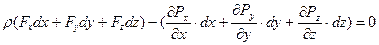(3.9)

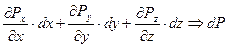
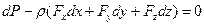(3.10)

Уравнение (3.10) называют основным уравнением гидростатики в дифференциальной форме. Пусть из массовых сил на данный объем жидкости в форме параллелепипеда действует только сила тяжести. Запишем уравнение Эйлера (3.10)

;

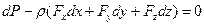Сила тяжести направлена по нормали к осям и в обратную сторону оси .

Получим основное уравнение статики

(3.12)

После интегрирования

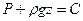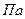, (3.13)

где - постоянная интегрирования.

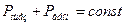(3.14)

где 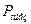- потенциальная энергия единицы объема жидкости;

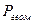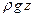= - потенциальная энергия положения единицы объема жидкости.