Квантовые числа. Для характеристики поведения электрона в атоме введены квантовые числа: главное, орбитальное, магнитное и спиновое.
Для характеристики поведения электрона в атоме введены квантовые числа: главное, орбитальное, магнитное и спиновое.
Главное квантовое число n определяет энергию электрона на энергетическом уровне и размер атомной орбитали. Оно может принимать целочисленные значения от 1 до  (практически от 1 до 7 соответственно номеру периода, в котором находится элемент). Чем больше n, тем больше энергия электрона и размер атомной орбитали (электронного облака).
(практически от 1 до 7 соответственно номеру периода, в котором находится элемент). Чем больше n, тем больше энергия электрона и размер атомной орбитали (электронного облака).
Энергия электрона, главным образом, зависит от расстояния электрона от ядра: чем ближе к ядру находится электрон, тем меньше его энергия и размер электронного облака.
Состояние электрона, характеризующееся определённым значением главного квантового числа, принято называть энергетическим уровнем электрона в атоме. Энергетические уровни обозначают прописными буквами согласно схеме:
Значение n : 1 2 3 4 5 6 7.
Обозначение: K,L,M,N,O,P,Q.
Так, если n=3, то электрон находится на третьем уровне от ядра или на М уровне и, наоборот, для пятого уровня (О – уровня) n=5.
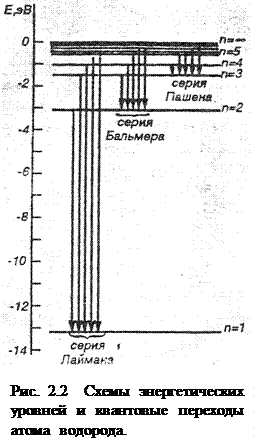
Конечно, никаких уровней в атоме нет; говоря так, понимают лишь энергетическое состояние электрона, что и определяет его положение в атоме. Электроны, характеризующиеся одним и тем же значением главного квантового числа, образуют в атоме электронные облака приблизительно одинаковых размеров, поэтому можно говорить о существовании в атоме электронных слоев, или электронных оболочек, отвечающих определенным значениям главного квантового числа. При переходе электрона с уровня на уровень выделяются или поглощаются кванты энергии, которые могут проявиться в виде линий спектров (рис. 2.2) .
Было установлено, что энергетические уровни расщепляются на энергетические подуровни.
Согласно квантово – механическим расчётам, электронные облака отличаются не только размерами, но и формой.
Орбитальное квантовое число l характеризует форму атомной орбитали (электронного облака) и энергию электрона на энергетическом подуровне.
 |
Состояния электрона, характеризующиеся различными значениями орбитального квантового числа l принято называть энергетическими подуровнями электрона в атоме (подоболочками ). Как и n, l квантуется, т.е изменяется только целочисленно, принимая значения от 0 до (n-1), где n – главное квантовое число, всего n значений.
Энергетические подуровни обозначают буквами:
значение l : 0 1 2 3 4 5;
обозначение подуровня : s p d f g h.
В соответствии с этими обозначениями говорят об s - подуровне, p – подуровне и т.д. Число подуровней равно номеру уровня. Например:
| Уровень | n | l | Число подуровней | Обозначение подуровней в уровне |
| 1s | ||||
| 0, 1 | 2s, 2p | |||
| 0, 1, 2 | 3s, 3p, 3d | |||
| 0, 1, 2, 3 | 4s, 4p, 4d, 4f |
То есть орбитальное квантовое число l описывает структуру энергетического уровня.
Электроны с орбитальным квантовым числом 0 называются s – электронами. Орбитали (электронные облака) имеют сферическую форму (рис. 2.3, а).
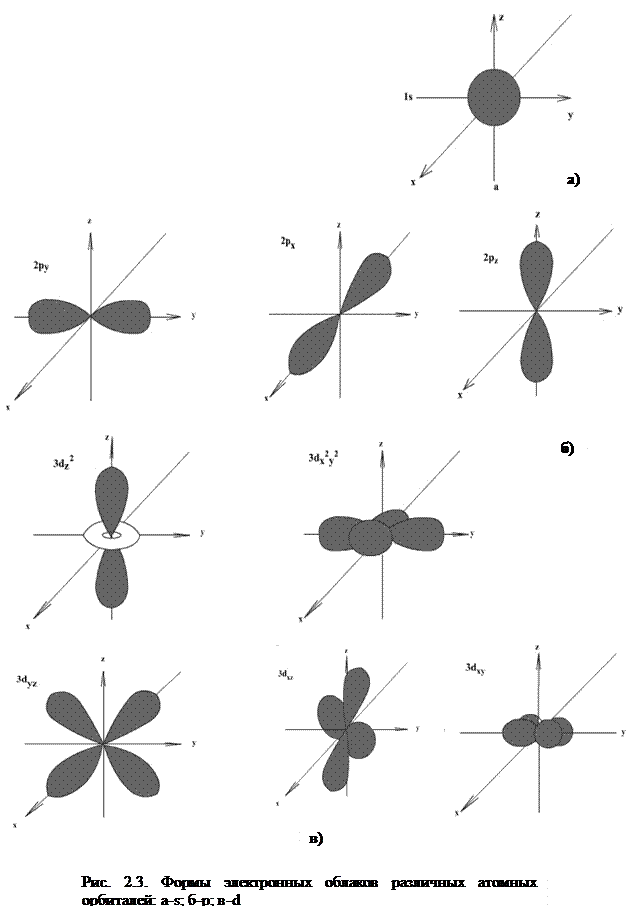 Электроны с орбитальным квантовым числом 1 называются p – электронами. Орбитали имеют «гантелевидную» форму (рис. 2.3,б).
Электроны с орбитальным квантовым числом 1 называются p – электронами. Орбитали имеют «гантелевидную» форму (рис. 2.3,б).
Электроны с l=2 называют d – электронами. Орбитали имеют форму сложной «четырехлепестковой» фигуры (рис. 2.4, в).
Электроны с l=3 получили название f – электронов. Форма их орбиталей ещё сложнее, чем форма d – орбиталей.
В одном и том же энергетическом уровне энергия подуровней возрастает в ряду ES<EP<Ed<Ef.
Магнитное квантовое число ml характеризует пространственную ориентацию атомной орбитали и связано с числом l, квантуется и принимает целочисленные значения, от -l до +l, включая ноль. Число значений ml равно 2l+1. Это число орбиталей с данным значением l, т.е. число энергетических состояний, в которых могут находиться электроны данного подуровня.
Внешнее магнитное поле изменяет пространственную ориентацию электронных облаков, поэтому при воздействии магнитного поля происходит расщепление энергетических подуровней электронов. В магнитном поле наблюдается расщепление атомных спектральных линий.
Определим число состояний (орбиталей) электронов в соответствующем подуровне:
| Подуровень | Орбитальное квантовое число l | Магнитное число ml | Число орбиталей с данным l |
| s p d f | -1, 0, +1 -2, -1, 0, +1, +2 -3, -2, -1, 0 ,+1, +2,+3 | 2l+1 |
Общее число состояний (орбиталей) на уровне равно n2. На рис. 2.3 показаны формы и ориентация в пространстве 1s –, 2p –, 3d – орбиталей.
На основе представлений о квантовых числах можно уточнить определение атомной орбитали (АО): совокупность положений электрона в атоме, характеризуемых определёнными значениями квантовых чисел n,l и ml: называют атомной орбиталью (АО). Условно АО обозначают в виде клеточки (энергетической или квантовой ячейки) – □. Соответственно, для s – подуровня одна АО – □, для p – подуровня три АО – □□□, для d – подуровня пять АО – □□□□□, для f – подуровня семь АО – □□□□□□□.
Изучение тонкой структуры атомных спектров показало, что, кроме различия размеров облаков, их формы и характера расположения в пространстве относительно друг друга, электроны различаются спином. Упрощенно спин можно представить как собственное вращение электрона вокруг своей оси (от англ. spin – веретено).
Спиновое квантовое число ms характеризует собственный момент количества движения электрона, обусловленный его движением вокруг своей оси; ms =± 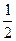 .
.
Знаки “+” и “–“ соответствуют различным направлениям вращения электрона – по или против часовой стрелки. Электроны с разными спинами называются антипараллельными или спаренными и обозначаются противоположно направленными стрелками ↑↓. Неспаренный электрон изображается одной стрелкой.
Итак, состояние электрона в атоме полностью характеризуется четырьмя квантовыми числами: n, l, ml и ms.
Дата добавления: 2015-04-19; просмотров: 3060;
