Лекция 5.

Уравнение установившегося движения элементарной струйки идеальной жидкости (уравнение Д.Бернулли)

В 1738 году Почетный член Петербургской Академии наук Даниил Бернулли опубликовал свою монографию «Гидродинамика, или записки о силах и движениях воды». В этой монографии, применив к движущейся в элементарной струйке идеальной жидкости теорему теоретической механики об изменении кинетической энергии (теорему «живых сил»), Д.Бернулли получил уравнение движения, известное ныне как уравнение Бернулли.

Это же уравнение можно получить, решая систему дифференциальных уравнений движения идеальной жидкости – уравнений Л. Эйлера. В данном случае мы воспользуемся этим способом. Для этого элементарную струйку идеальной жидкости расположим относительно координатных осей (рис. 23).

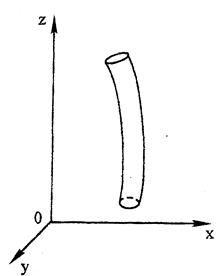
Рис. 23. Элементарная струйка

Умножим все члены, входящие в систему дифференциальных уравнений Л. Эйлера (56), соответственно на , после чего сложим все уравнения. В итоге получим:

. (63)

Для случая установившегося движения, когда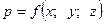

.

Учитывая, что

а

уравнение (63) получает следующий вид:

(63, а)

Рассмотрим случай, когда массовой силой, действующей на жидкость, является только сила веса. В этом случае (рис. 23) , а уравнение (63, а) получает вид:

Проинтегрировав это уравнение и разделив его левую и правую часть на , получим

, (64)

Так как сумма постоянна для всех частиц идеальной жидкости, то для двух произвольно взятых живых сечений элементарной струйки движущейся жидкости можно записать:

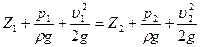(65)

Уравнение 65 называется уравнением движения Д. Бернулли; оно устанавливает связь между давлением, скоростью движения и геометрическим положением частиц идеальной жидкости элементарной струйки. В уравнении 65:

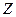
		- высота расположения рассматриваемой точки над произвольно выбранной горизонтальной плоскостью – плоскостью сравнения;
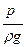
		- приведенная высота гидродинамического давления; так же как в гидростатике эту высоту называют пьезометрической;
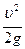
		- скоростной напор.

В гидродинамике сумму называют полным гидродинамическим напором сечения элементарной струйки. Из уравнения (65) следует, что для установившегося движения идеальной жидкости полный гидродинамический напор остается постоянным во всех сечениях элементарной струйки.